Билет 10

1. Признаки параллелограмма:

1. Е сли в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.

Доказательство. Пусть в четырёхугольнике АВСD стороны АD и СB параллельны и равны. Проведём диагональ АС, делящую параллелограмм на два треугольника: АВС и СDА. Эти треугольники равны по первому признаку, значит, их соответствующие углы равны. Тогда углы BAC и DCA равны как внутренние накрест лежащие при пересечении прямых АB и CD секущей АС, значит, АB||CD. Следовательно, АВСD – параллелограмм.

2. Е сли в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник – параллелограмм.

Доказательство. Проведём диагональ АС данного четырёхугольника АВСD, делящую его на треугольники АВС и СDА. Эти треугольники равны по третьему признаку, поэтому углы АCВ и СAD равны, значит АВ||CD. Т.к. АВ и СD равны и параллельны, то по первому признаку АВСD – параллелограмм.

3. Е сли в четырёхугольнике диагонали пересекаются и точкой пересечения делятся напополам, то этот четырёхугольник – параллелограмм.

Доказательство.

.

Аналогично, .

Противоположные стороны попарно равны, значит, ABCD – параллелограмм.

4. В параллелограмме удвоенная сумма квадратов сторон равна сумме квадратов диагоналей:

Доказательство.

Воспользуемся теоремой косинусов:

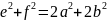
Теорема доказана.

2. П остроение треугольника по трём сторонам.

1. Отложить на плоскости отрезок BC=a.

2. Построить окружность с центром в точке B с радиусом c.

3. Построить окружность с центром в точке C с радиусом b.

4. Отметить точку A – одно из пересечений окружностей.

ABC – требуемый треугольник.

Билет №11

1. Параллелограмм. Свойства параллелограмма с доказательством.

О пределение. Параллелограмм – это четырёхугольник, противоположные стороны которого попарно параллельны.

Свойство 1. Любая диагональ параллелограмма делит его на два равных треугольника.

Доказательство. По II признаку (накрест лежащие углы и общая сторона).

Теорема доказана.

Свойство 2. В параллелограмме противолежащие стороны равны, противолежащие углы равны.

Доказательство. Аналогично,

Теорема доказана.

Свойство 3. В параллелограмме диагонали точкой пересечения делятся пополам.

Доказательство.

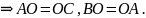
Теорема доказана.

С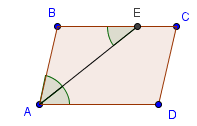 войство 4. Биссектриса угла параллелограмма, пересекая противоположную сторону, делит его на равнобедренный треугольник и трапецию. (Ч. сл. – вершину – два равнобедренных ∆-ка).

Доказательство.

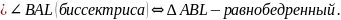
Т еорема доказана.

Свойство 5. В параллелограмме отрезок с концами на противоположных сторонах, проходящий через точку пересечения диагоналей, делится этой точкой пополам.

Доказательство.

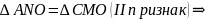
Теорема доказана.

С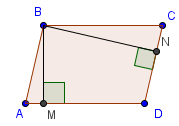 войство 6. Угол между высотами, опущенными из вершины тупого угла параллелограмма, равен острому углу параллелограмма.

Доказательство.

Т еорема доказана.

Свойство 7. Сумма углов параллелограмма, прилежащих к одной стороне, равна 180°.

Доказательство.

Теорема доказана.