Билет №5

1. Т еорема об углах, образованных при пересечении двух параллельных прямых третьей

Теорема. Если две параллельные прямые пересечены третьей прямой, то накрест лежащие углы равны, сумма односторонних углов равна 180°, сумма соответственных углов равна 180°.

Доказательство. Пусть а и b – параллельные прямые, и с – прямая, пересекающая их соответственно в точках А и В. Проведём через точку А прямую а₁ так, чтобы накрест лежащие углы, образованные секущей c с прямыми а₁ и b, были равны.

По признаку параллельности прямых прямые а₁ и b параллельны. А так как через точку А проходит только одна прямая, параллельная прямой b, то прямая а совпадёт с прямой а₁.

Значит, внутренние накрест лежащие углы, образованные секущей c параллельными прямыми а и b, равны.

Теорема доказана.

Из свойства углов, образованных при пересечении параллельных прямых секущей, следует, что если прямая перпендикулярна одной из параллельных прямых, то она перпендикулярна другой.

2. Вывод формулы площади треугольника

Воспользуемся формулой

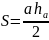
Если угол C острый, то .

Если угол C тупой, то .

Если угол C прямой, то

Следовательно,

Билет №6

1. В нешний угол треугольника (определение). Теорема о внешнем угле треугольника. Сумма внешних углов n-угольника.

Определение. Внешним углом называется угол, смежный с каким-нибудь углом треугольника.

Теорема. Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Доказательство. Пусть АВС – данный треугольник. По теореме о сумме углов треугольников ∠A+∠В+∠C=180°, значит, ∠А + ∠В = 180°-∠С, а 180°-∠С не что иное, как градусная мера внешнего угла при вершине С.

Теорема доказана.

Теорема. Сумма внешних углов n-угольника (взятых по одному при каждой вершине) равна 360°.

Доказательство. Из теоремы о сумме углов выпуклого n-угольника следует:

Теорема доказана.

2. Н ахождение значений синуса, косинуса и тангенса угла в 45°.

Возьмём прямоугольный треугольник с В нём, как в прямоугольном треугольике, . , значит, треугольник равнобедренный, .

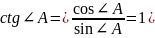
Билет №7

1. Геометрическое место точек. Теорема о геометрическом месте точек, равноудалённых от двух данных точек, в геометрической и аналитической формах.

Определение. Геометрическое место точек – фигура, которая состоит из всех точек на плоскости, обладающих определённым свойством.

Теорема. Геометрическое место точек, равноудалённых от двух данных точек, есть серединный перпендикуляр к отрезку, соединяющему эти точки, то есть прямая, перпендикулярная этому отрезку и проходящая через его середину.

Доказательство.

1. П усть точка C равноудалена от A и B. Отметим точку M – середину отрезка AB. Треугольники ACM и BCM равны по трём сторонам. Углы AMC и BMC равны и дают в сумме развёрнутый угол. Значит, они оба равны 90°. Мы доказали, что все точки, равноудалённые от двух данных точек, лежат на серединном перпендикуляре.

2. Пусть точка C лежит на серединном перпендикуляре к AB. Треугольники AMC и BMC равны двум катетам, значит, AC=BC. Мы доказали, что все точки серединного перпендикуляра к отрезку равноудалены от его концов.

Таким образом, геометрическое место точек, равноудалённых от двух данных точек, и серединный перпендикуляр к отрезку, соединяющему эти точки, совпадают.

Т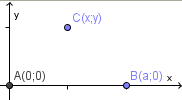 еорема доказана.

A (0; 0), B (a; 0), C (x; y). AC=CB.