Билет №1

1. Свойства равнобедренного треугольника, теорема о свойстве медианы, проведённой к основанию (равнобедренный треугольник)

1. углы при основании равны.

2. медиана, опущенная к основанию, является биссектрисой и высотой.

Доказательство:

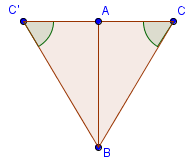
Пусть АВС - данный равнобедренный треугольник, АC - его основание, а BM – медиана, опущенная к нему.

Треугольники BAM и BCM равны по третьему признаку (3 стороны). Из равенства треугольников следует равенство углов. Угол ABM равен углу CBM, и угол AMB равен углу CMB. Так как углы ABM и CBM равны, то BM – Биссектриса. Так как углы AMB и CMB смежны и равны, то они прямые, значит, BM – Высота.

Теорема доказана.

2. Зависимость между стороной правильного многоугольника и радиусом описанной и вписанной окружности. Установление зависимости для квадрата, правильного треугольника и шестиугольника.

Квадрат

Равносторонний (правильный) треугольник:

Правильный шестиугольник:

Билет №2

1. Признаки равенства треугольников (доказательство всех)

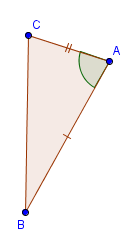
1. по двум сторонам и углу между ними

Доказательство:

Пусть у треугольников АВС и А₁В₁С₁ угол A равен углу А₁, АВ равно А₁В_1, АС равно А₁С₁. Докажем, что треугольники равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A₁B₁C₁ так, чтобы угол A совместился с углом A₁. Так как АВ=А₁В₁, а АС=А₁С₁, то B совпадёт с В₁, а C совпадёт с С_1. Значит, треугольник А₁В₁С₁ совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

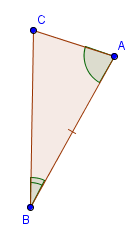
2. п о стороне и прилежащим к ней углам

Доказательство:

Пусть АВС и А₁В₁С_{1 –} два треугольника, у которых АВ равно А₁В_1, угол А равен углу А₁, и угол В равен углу В₁. Докажем, что они равны.

Наложим треугольник ABC (либо симметричный ему) на треугольник A₁B₁C₁ так, чтобы AB совпало с A₁B_1. Так как ∠ВАС =∠В₁А₁С₁ и ∠АВС=∠А₁В₁С₁, то луч АС совпадёт с А₁С₁, а ВС совпадёт с В₁С₁. Отсюда следует, что вершина C совпадёт с С_1. Значит, треугольник А₁В₁С₁ совпадает с треугольником АВС, а следовательно, равен треугольнику АВС.

Теорема доказана.

3. по трём сторонам

Д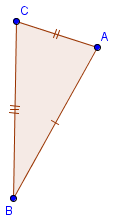 оказательство:

Рассмотрим треугольники ABC и A_lB_lC_1, у которых АВ=А₁В₁, BC = B_lC₁ СА=С₁А_1. Докажем, что ΔАВС =ΔA₁B₁C₁.

Приложим треугольник ABC (либо симметричный ему) к треугольнику A₁B₁C₁ так, чтобы вершина А совместилась с вершиной A₁, вершина В — с вершиной В₁, а вершины С и С₁, оказались по разные стороны от прямой А₁В₁. Рассмотрим 3 случая:

1. Луч С₁С про­ходит внутри угла А₁С₁В₁. Так как по условию теоремы стороны АС и A₁C₁, ВС и В₁С₁ равны, то треугольники A₁C₁C и В₁С₁С — равнобедренные. По теореме о свойстве углов равнобедренного треугольника ∠1 = ∠2, ∠3 = ∠4, поэтому ∠ACB=∠A₁C₁B₁.

2. Луч С₁С совпадает с одной из сторон этого угла. A лежит на CC₁. AC=A₁C₁, BC=B₁C₁, ∆C₁BC – равнобедренный, ∠ACB=∠A₁C₁B₁.

3. Луч C₁C проходит вне угла А₁С₁В₁. AC=A₁C₁, BC=B₁C₁, значит, ∠1 = ∠2, ∠1+∠3 = ∠2+∠4, ∠ACB=∠A₁C₁B₁.

Итак, AC=A₁C₁, BC=B₁C₁, ∠C=∠C₁. Следовательно, треугольники ABC и A₁B₁C₁ равны по первому признаку равенства треугольников.

Т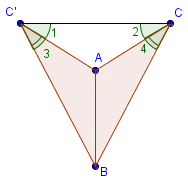 еорема доказана.