12. Апериодические сигналы. Прямое и обратное преобразование Фурье. Спектральные функции.
фотка,
Преобразование Фурье — операция, сопоставляющая функции вещественной переменной другую функцию вещественной переменной. Эта новая функция описывает коэффициенты («амплитуды») при разложении исходной функции на элементарные составляющие — гармонические колебания с разными частотами.
Полное формальное выражение преобразования Фурье:
... и обратное ему выражение:
Спектральная плотность S(ω) стационарного случайного процесса x(t) - это частотная функция, характеризующая спектральный (частотный) состав процесса, и представляет собой частотную характеристику для средних значений квадратов амплитуд гармоник, на которые может быть разложен случайный процесс. Спектральная плотность представляет собой двустороннее преобразование Фурье от корреляционной функции и имеет размерность [S(ω)]=в2/гц=в2с
.
13. Некоторые свойства спектральных функций.
Свойства спектральной плотности
Энергетический спектр стационарного процесса (вещественного или комплексного) – неотрицательная величина:
|
(7) |
.Энергетический спектр вещественного стационарного в широком смысле случайного процесса есть действительная и четная функция частоты:
|
(8) |
.Корреляционная функция
и
энергетический спектр 
стационарного
в широком смысле случайного процесса
обладают всеми свойствами, характерными
для пары взаимных преобразований
Фурье.
В частности, чем «шире» спектр
тем
«уже» корреляционная функция
,
и наоборот. Этот результат количественно
выражается в виде принципа или соотношения
неопределенности.
14. Одностороннее преобразование Фурье как частный случай преобразования Лапласа.
фотка
15. Спектры некоторых абсолютно интегрируемых сигналов. Спектр дельта-функции, треугольного импульса, полупериода синусоиды, экспоненты.
фотки
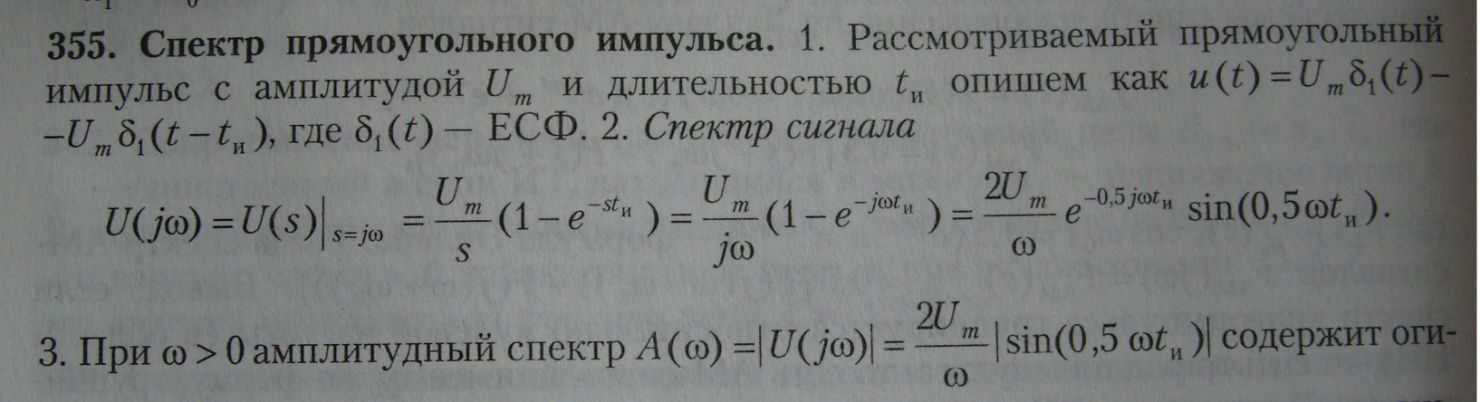
огибающую 2Um/w которая убывает пропорционально частоте w; начальное значение AC A(0)=S – равно площади импульса. 4. При W>0 фазовый спектр Ф(w)=argU(jw)=-0.5wtи + argsin(0,5wtи) – линейно изменяющая функция
16. Спектр единичной ступенчатой функции через предельный переход от спектра экспоненты.
после 21
1 2
3
4
1
7.
Теорема
Релея. Критерии практической ширины
спектра
2
1
4
3
6
5
1
8.
Влияние
длительности сигнала на ширину спектра
2
1
3
19. Влияние формы сигнала на ширину спектра
1
2
20. Использование преобразования Лапласа апериодического сигнала для получения преобразования Фурье и для разложения в ряд Фурье периодического сигнала той же формы
Непрерывное
преобразование Фурье эквивалентно
двустороннему преобразованию Лапласа
с комплексным аргументом 
:
Примечание: в
этих выражениях опущен масштабирующий
множитель 
,
который часто включается в определения
преобразования Фурье.
Связь между преобразованиями Фурье и Лапласа часто используется для того, чтобы определить частотный спектр сигнала или динамической системы.
1
2
4
3
21. Приближенный расчёт реакции спектральным методом
22. Идеальная неискажающая цепь
23. Интегрирующая цепь
24. Дифференцирующая цепь
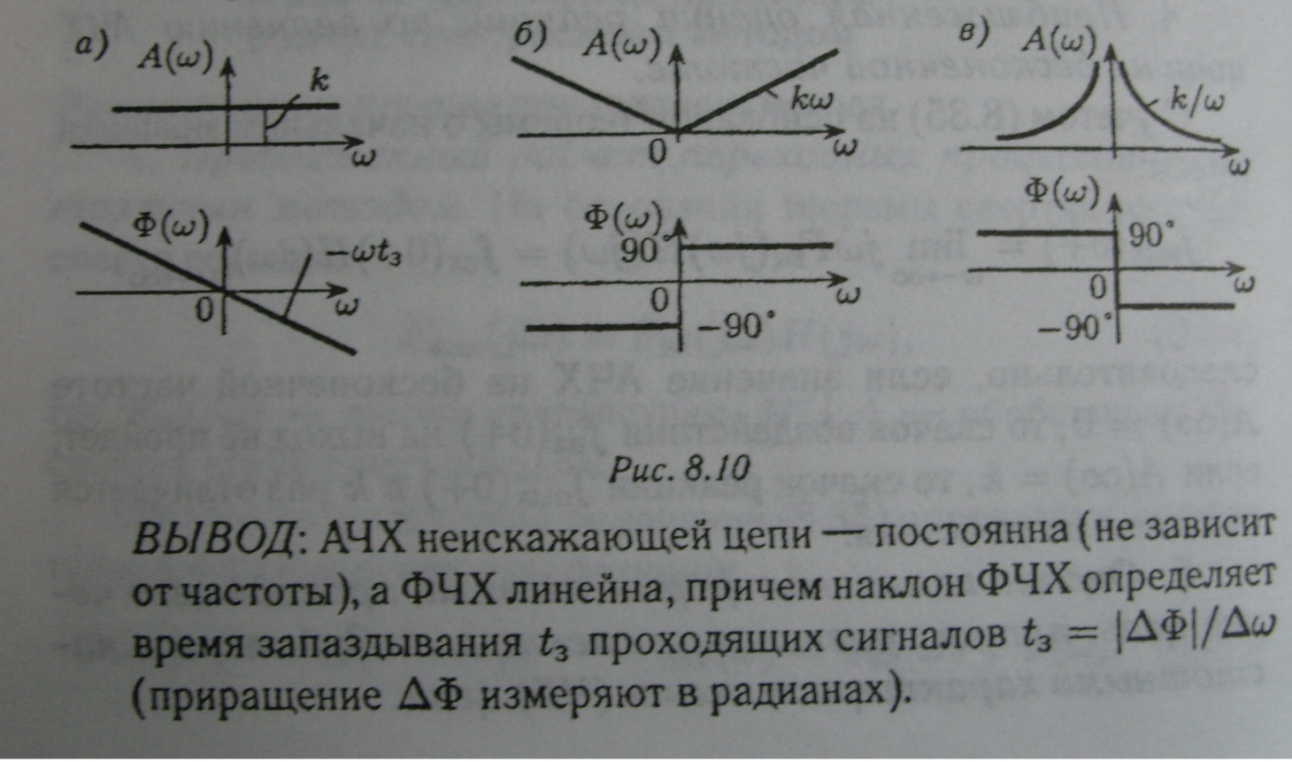
2
1
4
3
+ в тетради
25. Идеальный фильтр нижних частот
в тетради +
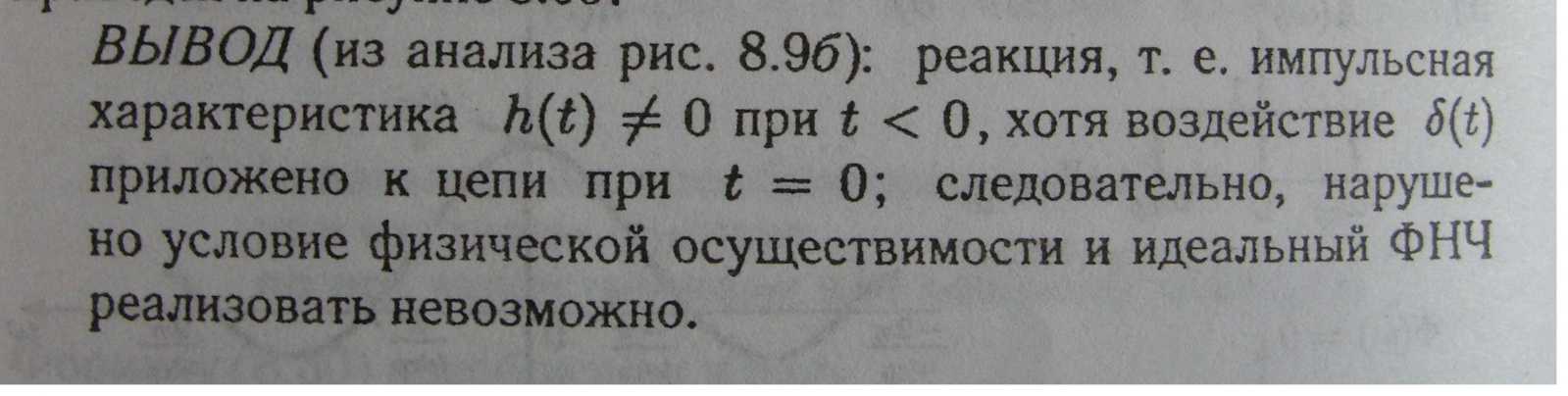
26. Теорема смещения в S-области. Спектры модулированных колебаний
в тетради
27. Четырёхполюсники. Общие сведения
28. Уравнения четырёхполюсника через параметры холостого хода
29. Уравнения четырёхполюсника через параметры короткого замыкания
30 . Уравнения четырёхполюсника через параметры передачи
1
5
<4
4
