ВОПРОСЫ К ТЕОРЕТИЧЕСКОМУ
ЗАЧЕТУ
для групп 1361, 1362, 1363, 1372, 1373
Преобразование Лапласа. Операторные схемы замещения.
Получение оригиналов по изображениям.
Получение изображения некоторых импульсов.
Некоторые свойства передаточных функций. Какую информацию несут нули и полюсы передаточной функции.
Виды сигналов.
Ряд Фурье в тригонометрической форме.
Влияние различных видов симметрии на состав ряда.
Ряд Фурье в комплексной форме. Спектры периодических сигналов.
Мощность и действующее значение в установившемся периодическом режиме.
Приближенный расчёт в установившемся периодическом режиме.
Разложение в ряд Фурье периодической последовательности прямоугольных импульсов.
Апериодические сигналы. Прямое и обратное преобразование Фурье. Спектральные функции.
Некоторые свойства спектральных функций.
Одностороннее преобразование Фурье как частный случай преобразования Лапласа.
Спектры некоторых абсолютно интегрируемых сигналов. Спектр дельта-функции, треугольного импульса, полупериода синусоиды, экспоненты.
Спектр единичной ступенчатой функции через предельный переход от спектра экспоненты.
Теорема Релея. Критерии практической ширины спектра.
Влияние длительности сигнала на ширину спектра.
Влияние формы сигнала на ширину спектра.
Использование преобразования Лапласа апериодического сигнала для получения преобразования Фурье и для разложения в ряд Фурье периодического сигнала той же формы.
Приближенный расчёт реакции спектральным методом.
Идеальная неискажающая цепь.
Интегрирующая цепь.
Дифференцирующая цепь.
Идеальный фильтр нижних частот.
Теорема смещения в S-области. Спектры модулированных колебаний.
Четырёхполюсники. Общие сведения.
Уравнения четырёхполюсника через параметры холостого хода.
Уравнения четырёхполюсника через параметры короткого замыкания.
Уравнения четырёхполюсника через параметры передачи.
Последовательное, параллельное и каскадное соединения четырёхполюсника.
Цепи с магнитной связью. Общие сведения.
Последовательное соединение ИСЭ.
Параллельное соединение ИСЭ.
Схемное устранение магнитной связи.
Воздушный трансформатор. Передаточная функция по току, по напряжению, входное сопротивление.
Идеальный трансформатор. Коэффициент трансформации. Передача по току, по напряжению, входное сопротивление. Три основных использования трансформатора.
Схема замещения реального трансформатора.
Теорема дискретизации (Котельникова).
Частично.
Преобразование Лапласа. Операторные схемы замещения.
Сущность операторного метода заключается в том, что функции вещественной переменной t, которую называют оригиналом, ставится в соответствие функция комплексной переменной p, которую называют изображением. В результате этого производные и интегралы от оригиналов заменяются алгебраическими функциями от соответствующих изображений (дифференцирование заменяется умножением на оператор р, а интегрирование – делением на него), что в свою очередь определяет переход от системы интегро-дифференциальных уравнений к системе алгебраических уравнений относительно изображений искомых переменных. При решении этих уравнений находятся изображения и далее путем обратного перехода – оригиналы.
Центральным принципом решения переходного процесса операторным методом является преобразования обычной электрической схемы к операторной схеме замещения переменной p. Полученную схему рассчитывают любым известным методом (методом узловых потенциалов, контурных токов или эквивалентных преобразований например).
На рисунках ниже приведена схема электрической цепи и её операторная схема замещения соответственно:
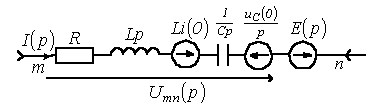
Таким образом правила преобразования основных элементов электрической цепи:
Активное сопротивление остаётся без изменений
Конденсатор ёмкостью C заменяется двумя элементами — конденсатором 1/pC и источником ЭДС Uc(0)/p, который характеризует начальный заряд на конденсаторе
Индуктивность L заменяется двумя элементами — Индуктивностью pL и источником ЭДС L·iL(0), который характеризует начальный ток через индуктивность
П
остоянный
источник ЭДС или тока J, E заменяются на
J/p и E/p соответственно
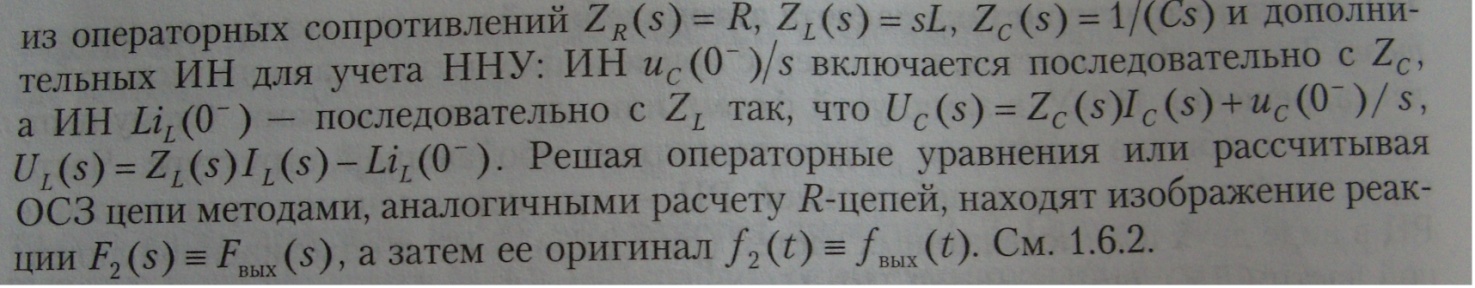
2. Получение оригиналов по изображениям
Для определения оригинала по изображению самым общим (и самым сложным) методом является взятие интеграла обратного преобразования Лапласа:
Рис. 1
Величина С>0
в пределах интеграла ограничивает на
комплексной плоскости область
интегрирования (рис.1). Значение
постоянной С определяется
характером функцииS(p)ept :
путь интегрирования (на рис.1 он проходит
по прямой С-j 
, C+j
)
должен проходить правее полюсов этой
функции.
Можно вместо прямого пути интегрирования образовать замкнутый контур (пунктир на рис.1) добавлением дуги конечного радиуса, причем величина этого радиуса должна быть такова, чтобы в контуре интегрирования оказались бы все полюса функции S(p). Для функций s(t),определенных для t>0, контур должен быть расположен в левой полуплоскости.
Получение оригинала в этом случае сводится к определению:
где 
- сумма вычетов в полюсах функции S(p) .
Вычет определяется следующим образом.
При наличии полюсов изображение всегда можно представить в виде отношения двух полиномов
Полюсами функции S(p) будут корни уравнения W(p)=0, т.е. нули знаменателя.
Если функция S(p) имеет в точке p1 простой полюс, то
Если полюс p1 имеет кратность m (m - целое положительное число), то
Более простым способом является использование таблиц соответствия оригинал-изображение для некоторых функций. В таблице 1 даны эти соответствия для некоторых часто встречающихся в радиоэлектронике сигналов.
Таблица 1
Оригинал (t>0) |
Изображение |
d (t) |
1 |
A |
|
e- a t |
|
1- e- a t |
|
t |
|
te- a t |
|
sin w t |
|
cos w t |
|
e- a t cos w 0t |
|
