3.4. Стационарная теплопередача через плоскую стенку

Пусть плоская однородная стенка имеет толщину  (рис. 3.2).

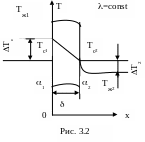
Заданы коэффициент теплопроводности материала стенки , температуры омывающей стенку жидкостей Т_ж1 и Т_ж2, а также коэффициенты теплоотдачи ₁ и ₂. Будем считать, что величины Т_ж1, Т_ж2, ₁ и ₂ постоянны и не меняются вдоль поверхности. Это позволяет рассматривать изменение температуры жидкостей и стенки только по оси Ох. На границах стенки заданы граничные условия третьего рода (3.5)

при x=0 q = ₁(Т_ж1 - Т_C1)

при x= q = ₂(Т_C2 – T_ж2)

Необходимо определить плотность теплового потока и температуры на поверхностях стенки.

Так как q = const в любой точке стенки, то, добавив к граничным условиям соотношение (3.12), запишем их в виде

Если сложить левые и правые части этих равенств, то получим следующее соотношение для плотности теплового потока

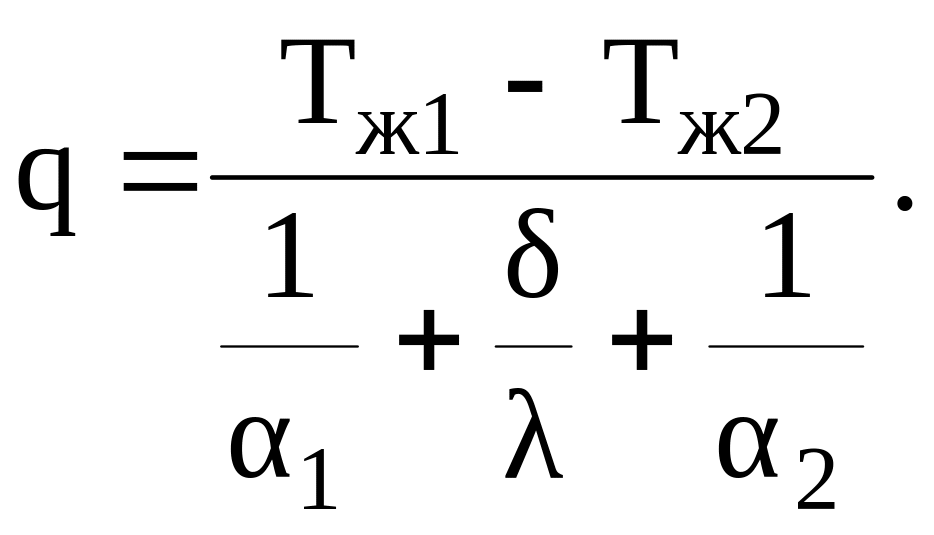(3.19)

Подставив найденное значение q в выше написанные равенства, определим температуры на поверхностях стенки Т_C1 и Т_C2. Величина

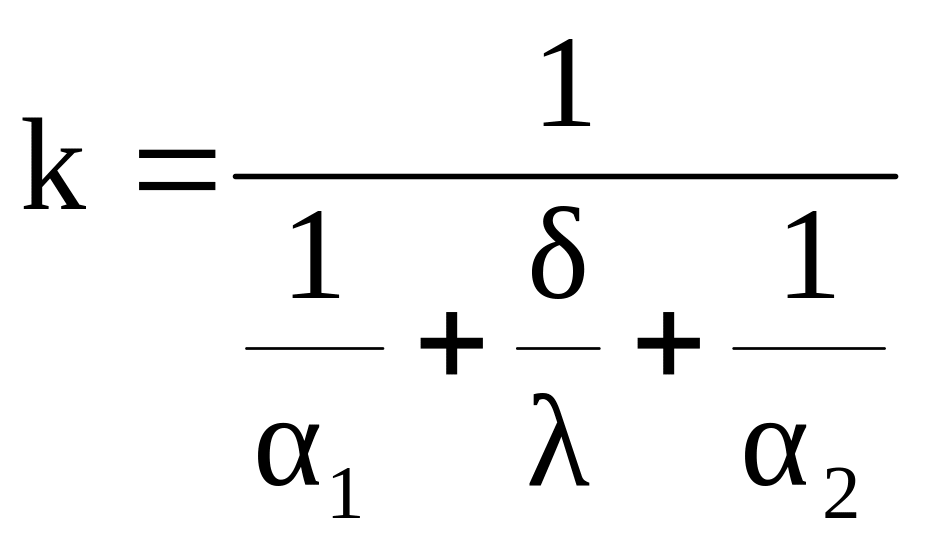(3.20)

получила название коэффициента теплопередачи. Величина, обратная коэффициенту теплопередачи, называется термическим сопротивлением теплопередачи

(3.21)

Из (3.21) видно, что полное термическое сопротивление теплопередаче складывается из частных термических сопротивлений: термического сопротивления теплоотдаче на левой поверхности стенки R_1=1/_1; термического сопротивления теплопроводности стенки R_C1=/ и термического сопротивления теплоотдаче на правой поверхности стенки R_2=1/_2. Очевидно, что для многослойной стенки нужно учитывать термическое сопротивление каждого слоя. Если стенка состоит из n слоев, то полное термическое сопротивление теплопередаче через такую стенку равно

(3.22)

Плотность теплового потока через многослойную стенку, состоящую из n слоев, будет равна

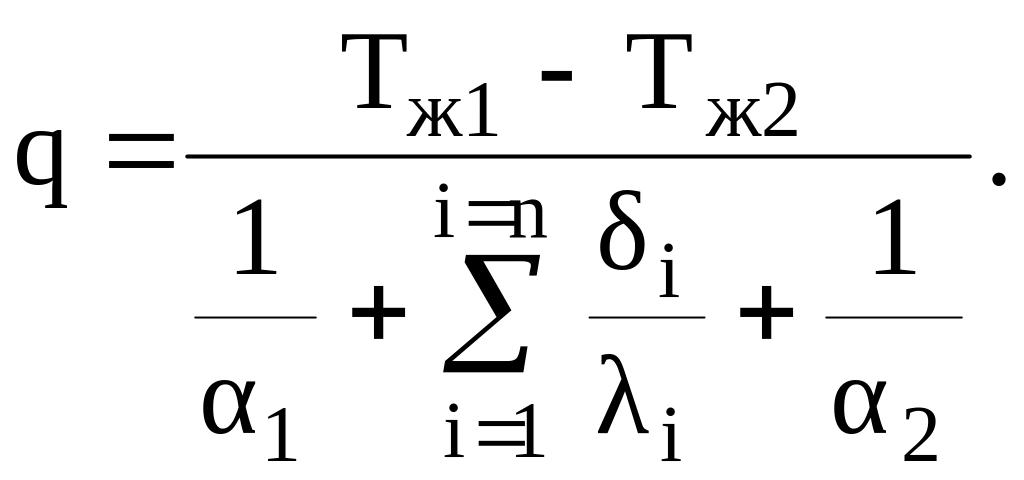(3.23)

Температуры на наружных поверхностях такой стенки составляют

(3.24)

Температура на границе любых двух слоев i и i+1 может быть определена по уравнению

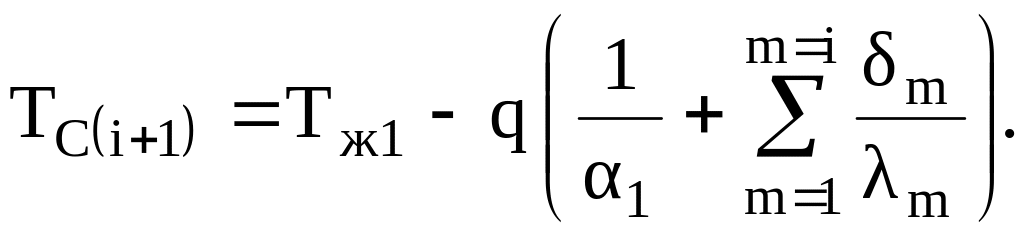(3.25)

Как видно из (3.24) – (3.23) и (3.17) при ₁= и ₂= граничные условия третьего рода вырождаются в граничные условия первого рода.

3.5. Стационарная теплопроводность через цилиндрическую стенку

П усть задана цилиндрическая стенка (труба) с внутренним диаметром d₁=2r₁ и наружным диаметром d₂=2r₂ , длина которой L (рис. 3.3). Коэффициент теплопроводности материала стенки  является постоянной величиной. На поверхностях стенки заданы постоянные температуры Т_С1 и Т_С2. Внутренние источники тепла отсутствуют q_V=0.

В рассматриваемом случае дифференциальное уравнение теплопроводности (3.4) удобно записать в цилиндрической системе координат:

(3.26)

При этом ось Oz совмещена с осью трубы. Так как температуры на наружной и внутренней поверхностях трубы неизменны, то изотермические поверхности являются цилиндрическими, имеющими с трубой общую ось. Температура изменяется только по радиусу трубы, поэтому имеем

(а)

С учетом (а) для нашего случая соотношение (3.26) имеет вид

(3.27)

Граничные условия:

при r=r₁ T=T_C1; при r=r₂ T=T_C2. (3.28)

Введем новую переменную u=dT/dr в соотношение (3.27)

(б)

Разделив переменные в (б) и проинтегрировав, получим

ln u + ln r = ln C₁. (в)

Потенцируя выражение (в) и переходя к первоначальным переменным, имеем выражение для градиента температуры

(г)

После интегрирования соотношения (г) получим

(д)

Как видно из соотношения (д) поле температуры, в отличие от плоской стенки, в зависимости от координаты не линейное, а логарифмическое. Причина этого в том, что, также как и в плоской стенке, поток тепла в стационарном режиме через цилиндрическую стенку постоянен. Однако у цилиндрической стенки, в отличие от плоской стенки, внутренняя и наружная поверхности не одинаковы. Поэтому градиент температуры (г) и, следовательно, плотность теплового потока не остаются постоянными, а зависят от радиуса. Постоянные С₁ и С₂ можно определить, подставив в (д) граничные условия (3.28)

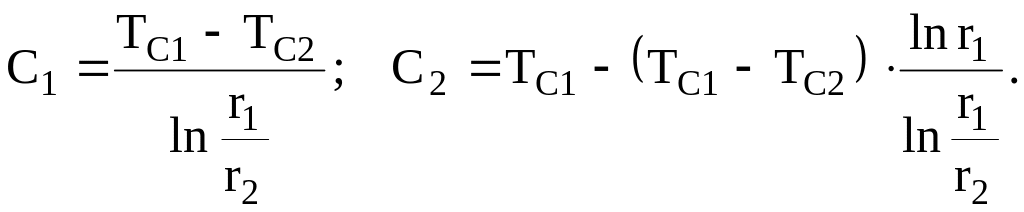(е)

Подставив значения С₁ и С₂ в соотношение (д), получим окончательно поле температуры в цилиндрической стенке при граничных условиях первого рода

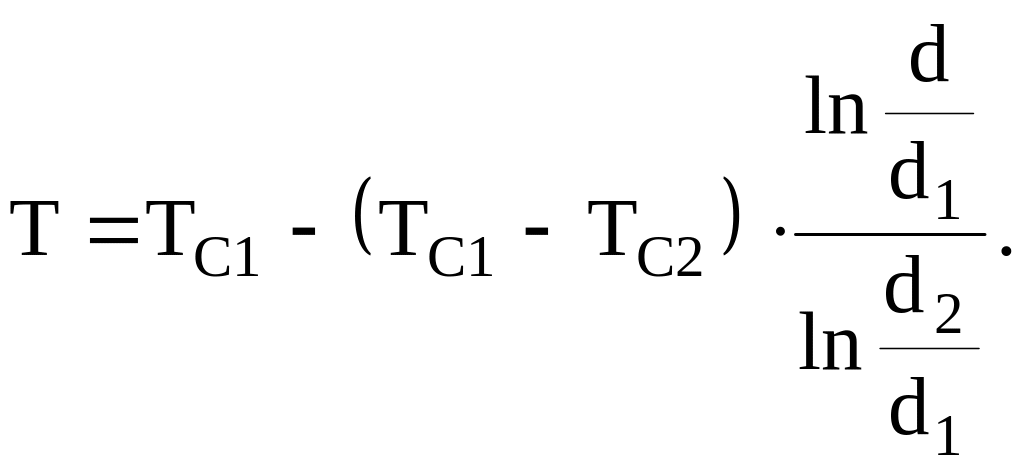(3.29)

Поток тепла, проходящего через любую изотермическую цилиндрическую поверхность площадью F, по закону Фурье равен

Подставляя в это уравнение соотношение (г) с учетом (е) и учитывая, что F=2rL, получим формулу для потока тепла через цилиндрическую стенку

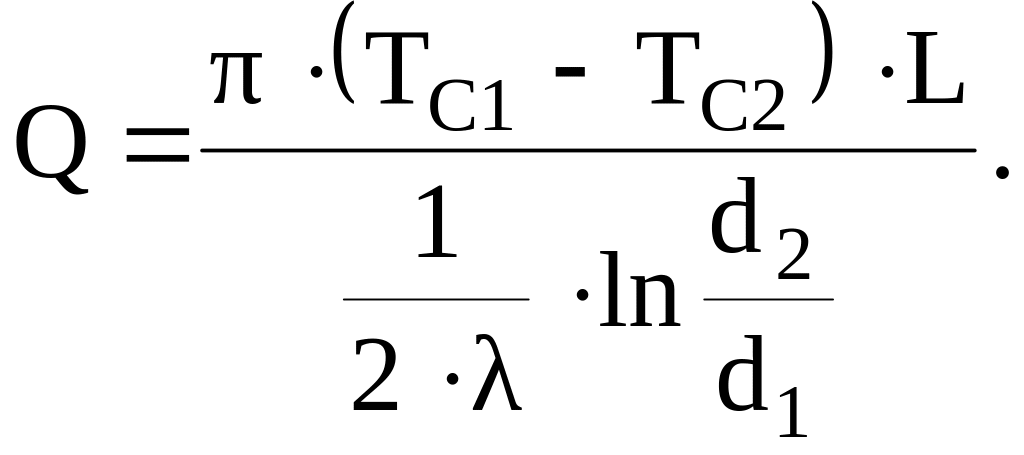(3.30)

Если отнести этот поток к внутренней поверхности трубы, то получим плотность теплового потока на внутренней поверхности

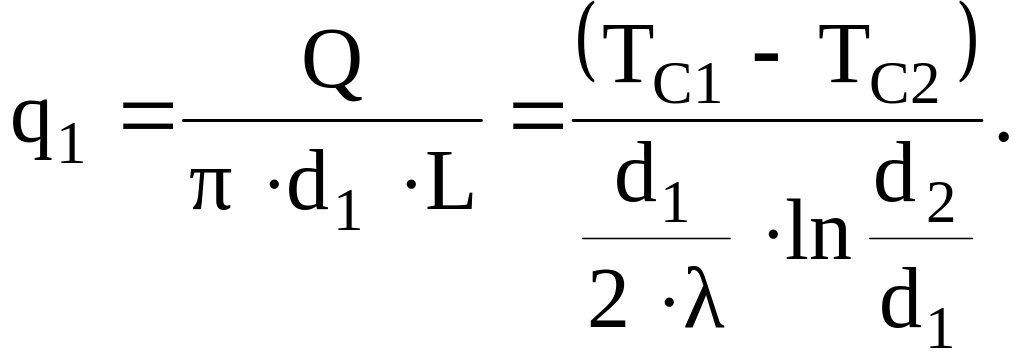(3.31)

Если отнести этот поток к наружной поверхности трубы, то получим плотность теплового потока на наружной поверхности

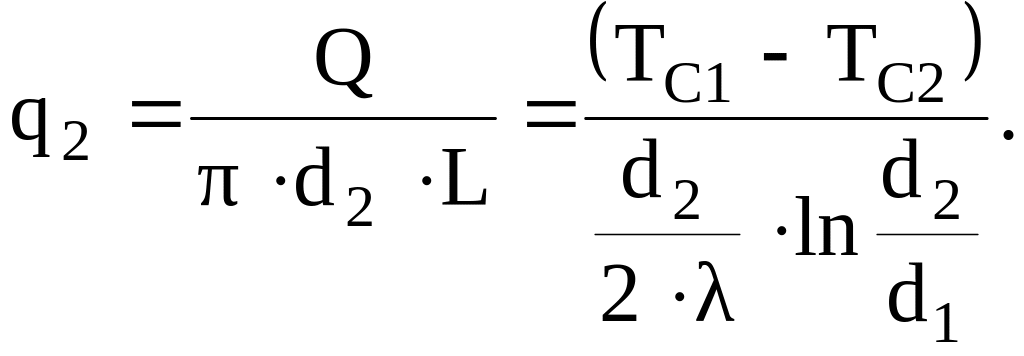(3.32)

Тепловой поток, отнесенный к единице длины трубы, называется линейной плотностью теплового потока

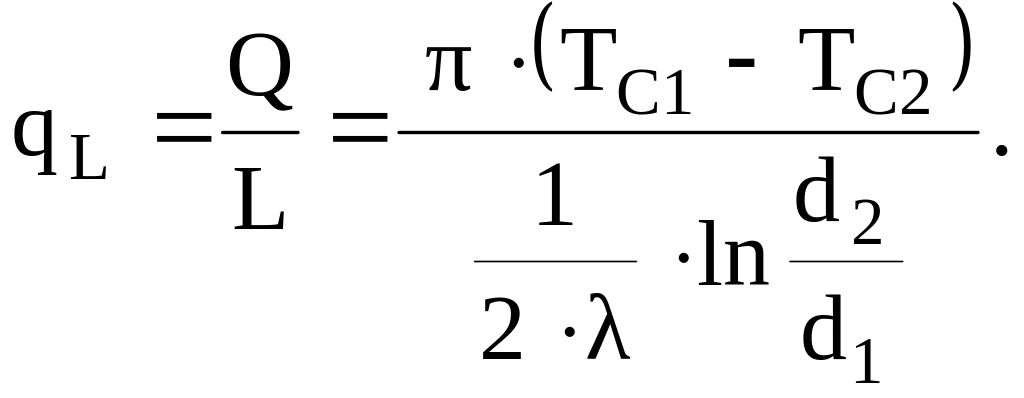(3.33)

Эта величина широко используется в расчетах цилиндрических стенок, так как она постоянна в любой точке стенки, в отличие от плотности теплового потока. Зная ее, можно определить плотности теплового потока по соотношению

(3.34)

Величина:

(3.35)

получила название линейного термического сопротивления теплопроводности цилиндрической стенки. Так как общее линейное термическое сопротивление состоит из частных линейных термических сопротивлений, то совершенно очевидно, что для многослойной цилиндрической стенки нужно учитывать линейное термическое сопротивление каждого слоя. Тогда линейная плотность теплового потока через многослойную цилиндрическую стенку, состоящую из n слоев, равна

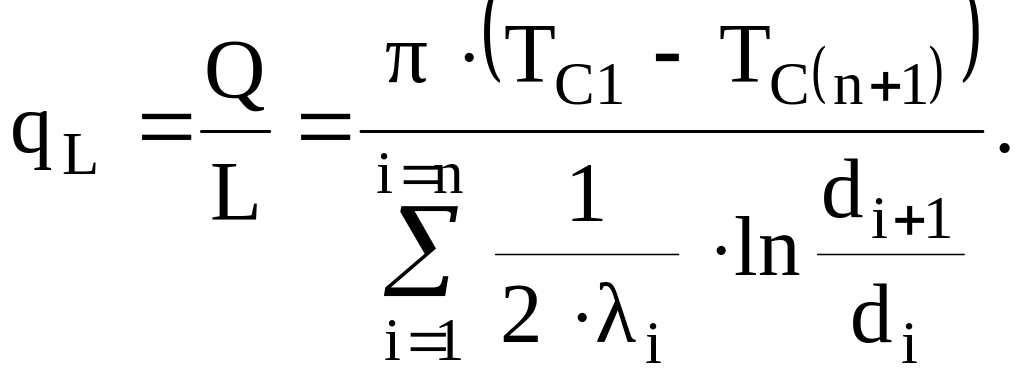(3.36)

По аналогии с плоской многослойной стенкой температура на границе любых двух цилиндрических слоев i и i+1 может быть определена по уравнению

(3.37)

Если коэффициент теплопроводности материала стенки является функцией температуры вида , то линейная плотность теплового потока определяется тем же соотношением (3.33), но вместо  в него надо подставить _СР, определяемое формулой

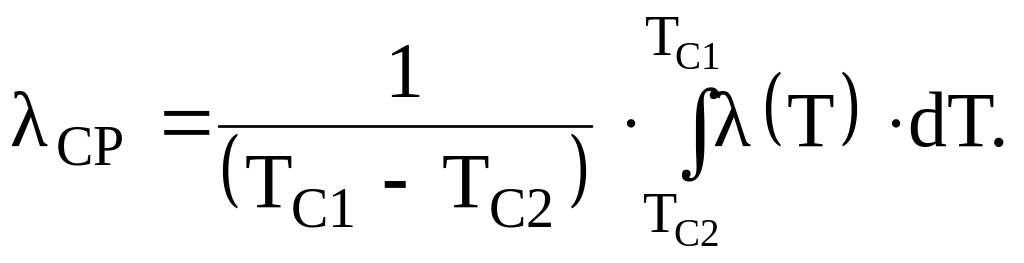(3.38)

В этом случае для нахождения температурного поля можно использовать уравнение Фурье, записанное для цилиндрической стенки

(3.39)

Если разделить переменные и проинтегрировать уравнение (3.39) в пределах от r=r₁ до r и от T=T_C1 до T и найти из полученного интеграла T, то получим следующее выражение для температурного поля

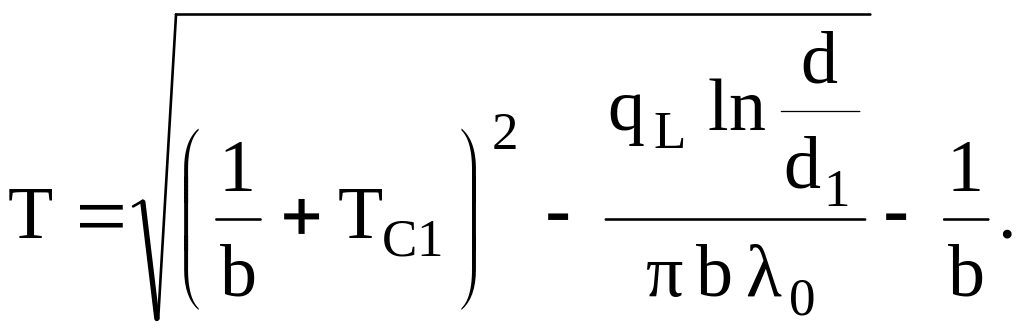(3.40)