3.3. Стационарная теплопроводность через плоскую стенку
Пусть имеем плоскую стенку толщиной с постоянным коэффициентом теплопроводности . На наружных поверхностях стенки поддерживают постоянными температуры ТС1 и ТС2. Если ось Ох направить, как показано на рис. 3.1, то при заданных условиях температура в направлении осей Оу и Oz будет оставаться постоянной
Рис. 3.1
В связи с этим температура будет зависеть только от одной координаты x, и дифференциальное уравнение теплопроводности (3.4) будет иметь вид
(3.7)
Граничные условия первого рода зададим следующим образом:
при x=0 T=TC1,
при x= T=TC2. (3.8)
Первое интегрирование (3.7) дает
(3.9)
После второго интегрирования получим
T=C1x+C2. (3.10)
Из уравнения (3.10) следует, что при постоянном коэффициенте теплопроводности поле температуры в стенке в зависимости от x изменяется по линейному закону. Постоянные С1 и С2 определяются из граничных условий (3.8) после их подстановки в (3.10)
Подставляя значения этих постоянных в уравнение (3.10), получим поле температуры в плоской стенке
(3.11)
Так как коэффициент теплопроводности и градиент температуры, в соответствии с (3.9), постоянны, то плотность теплового потока в любой точке стенки постоянна и по закону Фурье равна
(3.12)
Отношение / называется тепловой проводимостью стенки, а обратная величина / = RC – термическим сопротивлением теплопроводности стенки. Таким образом, плотность теплового потока прямо пропорциональна разности температур (температурному напору) и обратно пропорциональна термическому сопротивлению теплопроводности стенки. Поток тепла определяется по формуле
(3.13)
Количество тепла, перенесенное через плоскую стенку за время , определяется соотношением
(3.14)
Рассмотрим случай, когда коэффициент теплопроводности зависит от температуры = (t). Для многих материалов эта зависимость близка к линейной = О(1+bT), где О – значение коэффициента теплопроводности при 0оС. Подставляя это значение коэффициента теплопроводности в закон Фурье, имеем
(а)
Разделяя переменные и интегрируя выражение (а) в пределах от x = 0 до x = и в интервале температур от TC1 до TC2, получаем
(б)
В выражении (б) множитель
является средне интегральным значением коэффициента теплопроводности, т.е.
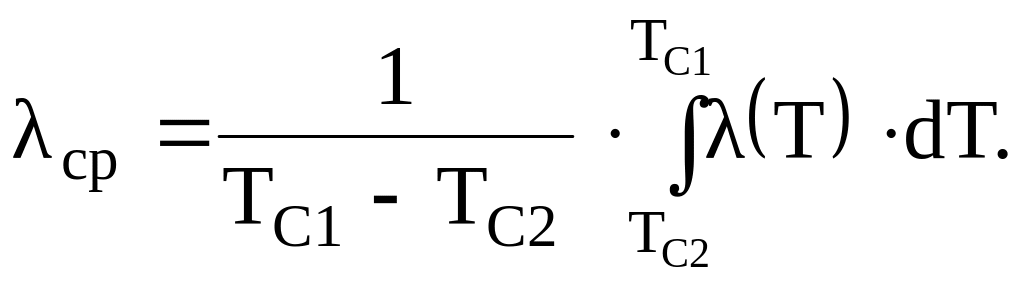(3.15)
При этом значении коэффициента теплопроводности плотность теплового потока рассчитывается по тому же соотношению (3.12). Интегрируя выражение (а) в пределах от x = 0 до любой текущей координаты x, а в интервале температур от ТС1 до T, получаем нелинейное выражение для температурного поля в стенке в зависимости от координаты x
(3.16)
Рассмотрим теплопроводность многослойной плоской стенки, состоящей из n однородных слоев. Будем полагать, что между слоями отсутствуют контактные термические сопротивления, т.е. температура на обеих соприкасающихся поверхностях двух слоев одинакова. Контактные термические сопротивления необходимо учитывать при больших плотностях теплового потока q25000 вт/м2 2. При стационарном режиме тепловой поток, проходящий через любую изотермическую поверхность неоднородной стенки, один и тот же.
В противном случае разность подведенного и отведенного потока тепла по закону сохранения энергии пошла бы на изменение энтальпии самой стенки и ее температура во времени не осталась бы постоянной. Так как у плоской стенки боковые поверхности одинаковы, то и плотность теплового потока при стационарном режиме во всех точках стенки q = const. При заданных температурах на внешних поверхностях такой стенки TC1 и TCn+1, толщине слоев i, где i = 1,2,….,n, и коэффициентах теплопроводности материалов этих слоев i можно, используя (3.12), для каждого слоя записать
……………………..
Если переписать эту систему равенств так, чтобы справа остались только температурные разности, а затем сложить левые и правые части, то при сложении правых частей все температуры, кроме первой и последней, сократятся, и получим окончательно для плотности теплового потока равенство
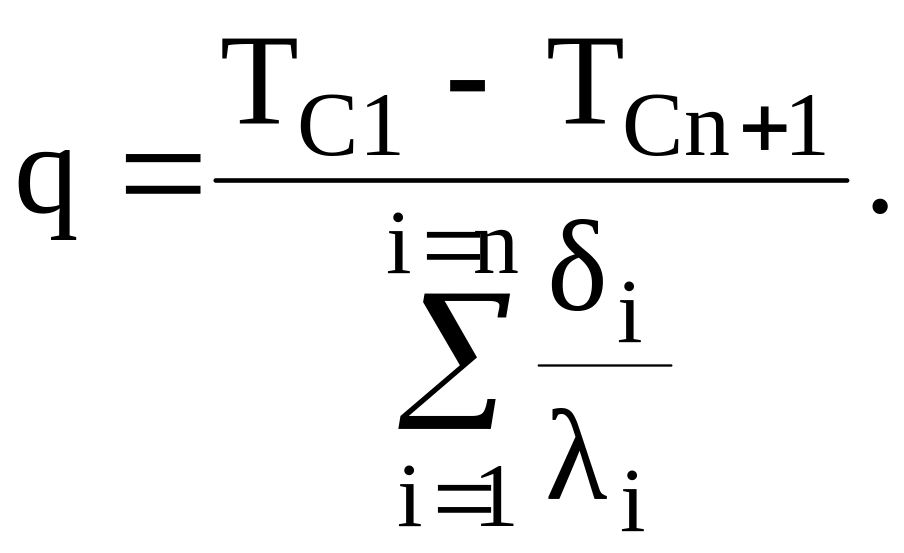(3.17)
Подставив найденное значение q в выписанные выше равенства, можно определить температуры на границах соприкосновения соседних слоев по формуле
(3.18)