5.6. Теплоотдача при внешнем обтекании тел

При внешнем обтекании тел форма их поверхности определяет формирование пограничного слоя, влияя тем самым на интенсивность теплоотдачи. Наиболее изучен теплообмен при вынужденном обтекании плоской пластины неограниченным внешним потоком жидкости. Как показано на рис. 5.1, толщина пограничного слоя, начиная от передней кромки поверхности, непрерывно возрастает. Коэффициент теплоотдачи напротив – уменьшается. На начальном участке пластины от х=0 до некоторого значения х=х_кр1 имеет место ламинарный режим течения жидкости в пограничном слое. Начиная с х=х_кр1 до некоторого значения х=х_кр2 на пластине имеет место переход ламинарного режима течения жидкости в турбулентное течение. Законы теплоотдачи при ламинарном и турбулентном режимах течения различны. Поэтому определение их границ имеет большое значение. Режим течения жидкости характеризуют критические значения числа Рейнольдса

Зная эти значения, можно определить х_кр1 и х_кр2, определяющие соответственно начало разрушения ламинарного течения и появление устойчивого турбулентного режима течения. Переход к турбулентному течению имеет место при значениях критического числа Рейнольдса от 10⁴ до 410⁶. Значения первого и второго критических чисел Рейнольдса зависят от интенсивности теплообмена, волнистости и шероховатости омываемой поверхности, удобообтекаемости передней ее кромки, вибрации поверхности.

В инженерной практике представляют интерес данные для среднего значения коэффициента теплоотдачи при внешнем обтекании пластины, которые были обобщены М. А. Михеевым в виде

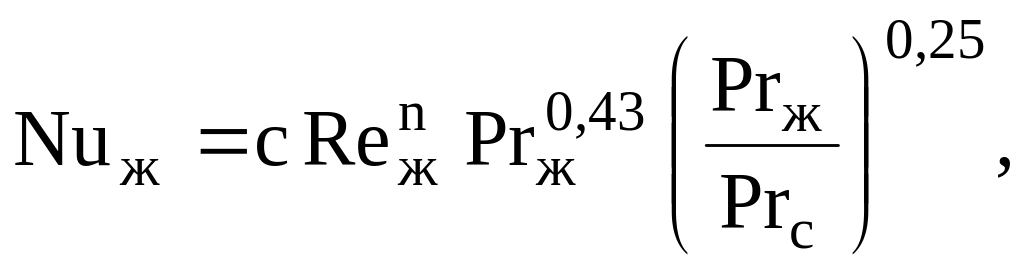(5.35)

где с и n зависят от величины числа Рейнольдса.

При

При внешнем вынужденном поперечном обтекании трубы на фронтовой части ее образуется пограничный слой. Толщина этого слоя растет, достигая наибольшей величины вблизи значения угла =90⁰, отсчитанного от лобовой точки. При 90⁰ происходит отрыв пограничного слоя от поверхности, и кормовая часть трубы омывается сильно завихренным потоком жидкости с обратными циркуляционными токами. Соответственно локальные значения коэффициента теплоотдачи максимальны в лобовой точке, где минимальна толщина пограничного слоя. С ростом угла  коэффициент теплоотдачи умень-шается, достигая минимальных значений вблизи участков поверхности, где пограничный слой достигает наибольшей толщины. После отрыва погранич-ного слоя от поверхности локальные значения коэффициента теплоотдачи вновь возрастают за счет вихрей в потоке, интенсифицирующих теплоотдачу.

Средняя теплоотдача для всей поверхности трубы может быть рассчитана по уравнению подобия

(5.36)

в котором при

В качестве определяющего размера в этом уравнении принят диаметр тру-бы. Число Рейнольдса рассчитывается по скорости невозмущенного потока w₀.

Если поток жидкости составляет с осью трубы угол , отличный от 90⁰, то коэффициент теплоотдачи, рассчитанный по этому уравнению, необходимо умножить на поправку _. Значение этой поправки при =3090⁰ можно определить по приближенной формуле

(5.37)

При обтекании жидкостью пучка труб теплоотдача зависит от расположения труб в пучке и номера ряда, в котором труба находится. Как правило, трубы в пучке располагают либо в шахматном, либо в коридорном порядке. При шахматном расположении труб имеет место более интенсивное перемешивание теплоносителя, что интенсифицирует теплоотдачу. Первый ряд труб и шахматного, и коридорного пучка обтекается не возмущенным потоком жидкости, поэтому для него имеет место наименьший коэффициент теплоотдачи. Характер обтекания остальных труб зависит от типа пучка. В коридорных пучках все трубы второго и последующих рядов находятся в вихревой зоне впереди стоящих труб. Однако циркуляция жидкости в вихревой зоне слабая, так как в основном жидкость проходит в продольных зазорах между трубами. В шахматных пучках обтекание глубоко расположенных трубок почти не отличается от обтекания трубок первого ряда. С достаточной для практики точностью можно считать, что третий и последующий ряды труб, при любом расположении труб в пучке, имеют одинаковый средний коэффициент теплоотдачи.

Если в качестве определяющего размера выбирать диаметр трубы, а число Рейнольдса рассчитывать по скорости в наиболее узком сечении пучка, то коэффициент теплоотдачи третьего и последующих рядов труб можно определить по формуле (5.36). При этом значения коэффициентов c и n зависят от вида пучка. При Re_ж=210²210⁵ для коридорного пучка с=0,23 и n=0,65; для шахматного пучка с=0,41 и n=0,6.

Коэффициенты теплоотдачи первого и второго рядов рассчитывают через коэффициент теплоотдачи третьего ряда. Для коридорного пучка труб ₁=0,6₃; ₂=0,9₃. Для шахматного пучка труб ₁=0,6₃; ₂=0,7₃. Когда скорость потока жидкости составляет с осями труб пучка угол 90⁰, то полученные из (5.36) коэффициенты теплоотдачи необходимо умножить на поправку _ (5.37).