5.5. Теплоотдача при вынужденном движении жидкости в трубах и каналах

Закономерности теплообмена со стенками трубы или канала зависят от режима течения жидкости. При Re10000 течение имеет развитый турбулентный характер. При этом у поверхности стенки образуется тонкий ламинарно текущий слой жидкости, а остальная часть потока представляет турбулентное ядро. При Re2000 в жидкости наблюдается ламинарный режим течения в изотермических условиях. При теплообмене такой режим течения может быть назван ламинарным только условно, так как свободная конвекция вызывает перемешивание жидкости. При Re=200010000 имеет место переходный режим течения.

Опытные данные по осредненной теплоотдаче при турбулентном режиме течения хорошо описываются формулой М.А. Михеева

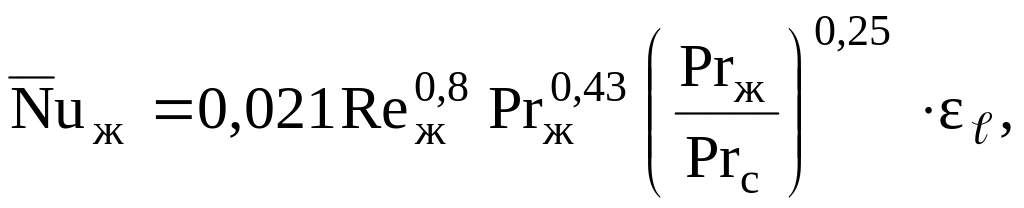(5.29)

которая справедлива при

Это уравнение справедливо для любой формы канала, в том числе для кольцевого (d₂/d₁=15,6) и щелевого (а/в=140). За определяющую температуру здесь взята средняя температура жидкости, о чем информирует индекс «ж». Индекс «с» в формуле говорит о том, что данный критерий рассчитывается по температуре стенки. Определяющий размер для круглых труб – диаметр, для каналов любого сечения – эквивалентный диаметр d_эк=4f/u, где u – периметр канала, f – площадь его поперечного сечения. Поправочный множитель _ учитывает теплоотдачу на начальном термическом участке трубы и может быть оценен по соотношению

(5.30)

где  – длина трубы;

d – диаметр трубы.

В изогнутых трубах центробежные силы вызывают дополнительную циркуляцию жидкости, и теплоотдача повышается. Коэффициент теплоотдачи в изогнутых трубах определяется как коэффициент теплоотдачи в прямых трубах, умноженный на поправку, которая подсчитывается по формуле

(5.31)

где d и R – диаметр трубы и радиус ее изгиба.

Для некоторых специфических случаев теплоотдачи в трубах получены и другие уравнения подобия. Так, при больших температурных напорах и Re30000 можно использовать формулу Дитрус Болтера

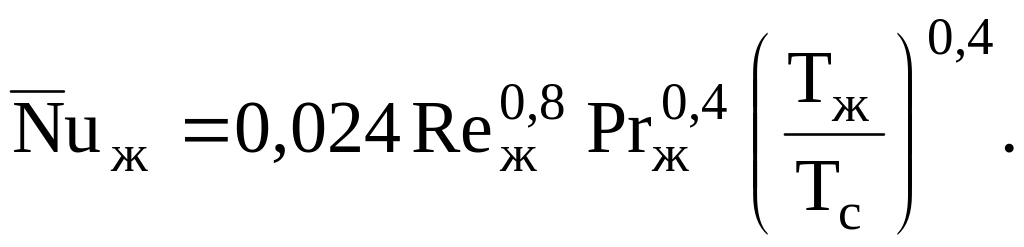(5.32)

За определяющую температуру здесь взята средняя температура жидкости, о чем информирует индекс «ж». Индекс «с» в формуле говорит о том, что данный критерий рассчитывается по температуре стенки. В качестве определяющего размера выбран диаметр или эквивалентный диаметр.

Для расчета теплоотдачи в трубах и каналах при М.А. Михеев рекомендует следующее уравнение подобия

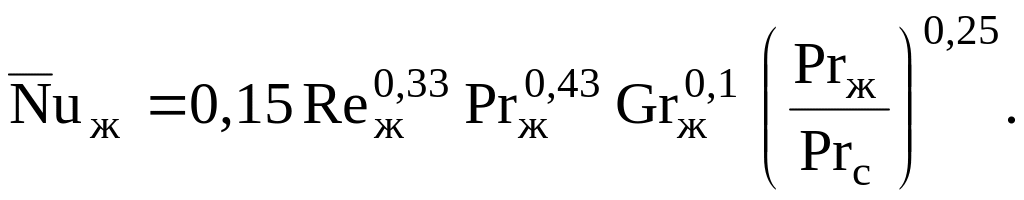(5.33)

Определяющие температура и линейный размер выбираются точно так же, как и в предыдущей формуле.

При переходном режиме течения теплоотдача не может быть описана единым уравнением подобия. Так как при этих условиях характер движения жидкости и теплообмена определяется не только величиной критерия Re , но и совокупностью тех воздействий, которым подвергался поток жидкости до поступления в рассматриваемый канал. Поэтому в общем случае для этой области можно определить только наиболее вероятные значения коэффициентов теплоотдачи с помощью уравнения подобия

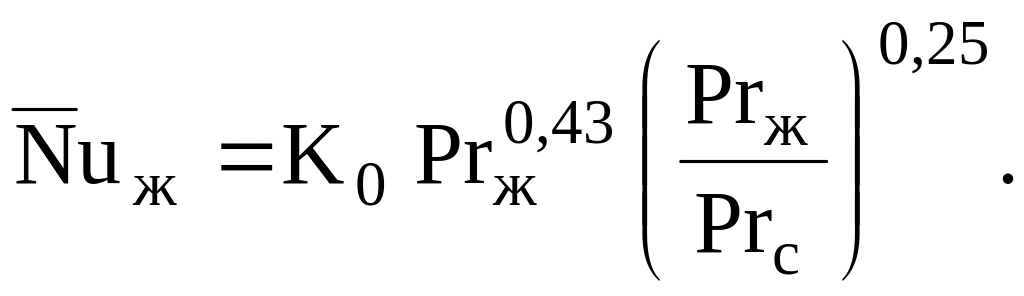(5.34)

За определяющую температуру здесь взята средняя температура жидкости, о чем информирует индекс «ж». Индекс «с» в формуле говорит о том, что данный критерий рассчитывается по температуре стенки. В качестве определяющего размера выбран диаметр или эквивалентный диаметр. Величина К₀ выбирается в зависимости от критерия Re из таблицы.

Re10-3	2,2	2,3	2,5	3.0	3,5	4	5	6	7	8	9	10
К0	2,2	3,6	4,9	7,5	10	12,2	16,5	20	24	27	30	33