4. Нестационарная теплопроводность

4.1. Общие положения

При нестационарном процессе теплопроводности или теплопередачи температура в каждой точке тела изменяется во времени. Если при стационарном режиме поток тепла, подводимый к телу, равен потоку тепла отводимому от тела, то при нестационарном режиме переноса тепла эти потоки не равны. Разность этих потоков тепла в соответствии с законом сохранения энергии расходуется на изменение энтальпии тела, что связано с изменением температуры во времени. Поэтому, в отличие от задач стационарной теплопроводности или теплопередачи, при решении уравнений (3.1) или (3.2) задают еще и начальные условия. Т.е. для того чтобы рассчитать, каким будет температурное поле в теле для некоторого момента времени, необходимо задать, каким оно было в некоторый начальный момент времени.

Однако для тел конечных размеров в случае постоянных, не зависимых от времени граничных условий, протекание процесса нестационарной теплопро-водности можно подразделить на две стадии. В первые моменты процесса характер изменения температуры различных точек тела во времени будет различным. Температура поверхности тела с начала процесса начнет приближаться к температуре окружающей среды, тогда как участки тела, удаленные от поверхности, могут некоторое время сохранять свою температуру или изменять ее в зависимости от начального распределения температур. Эта стадия процесса называется неупорядоченной. По истечении некоторого промежутка времени начальное распределение температур перестает влиять на характер протекания процесса. Закон изменения температуры во времени становится одинаковым для всех точек тела. Эту стадию процесса называют регулярным режимом.

При периодических во времени граничных условиях протекание процесса нестационарной теплопроводности также можно подразделить на две стадии. В стадии неупорядоченного режима температурное поле в теле зависит от начального распределения температур. По истечении некоторого промежутка времени в теле устанавливается квазистационарное температурное поле. Оно характеризуется тем, что в любой точке тела температура изменяется во времени, но ровно через период температура в любой точке тела принимает тоже значение.

Для определения температурного поля в телах классической формы (плоская неограниченная по длине и ширине стенка, неограниченный цилиндр, шар) используют аналитические методы решения. В телах сложной формы температурное поле определяют в результате численного интегрирования уравнений (3.1) и (3.2).

4.2. Охлаждение (нагревание) неограниченной пластины

Рассмотрим расчетные зависимости, полученные аналитическим методом [1,2,3], на примере охлаждения плоской стенки, размеры которой по длине и ширине настолько велики, что теплообменом с торцов можно пренебречь. При одинаковых условиях теплообмена на обеих поверхностях температурное поле будет одномерным и симметричным относительно середины стенки. Поэтому на рис. 4.1 ее толщина обозначена через 2.

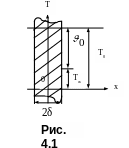
Будем полагать, что температура окружающей пластину жидкости Тж=const и коэффициент теплоотдачи = const. С учетом принятых ранее обозначений для избыточных температур дифференциальное уравнение (3.2) будет иметь вид

(4.1)

Н

Рис. 4.1

ачальные условия:

при (4.2)

При этом граничные условия в середине и на поверхности пластины соответственно можно записать так:

при х=0 (4.3)

при х= (4.4)

Решение этой задачи позволяет выразить безразмерную температуру в виде ряда

(4.5)

Здесь

Числа _n определяются из трансцендентного уравнения

(4.6)

где

Так как ₁, ₂,….., _n представляет собой ряд возрастающих чисел, то чем больше , тем меньше роль последующего члена ряда в (4.5) по сравнению с предыдущим. Кроме того, чем больше число Fo, тем быстрее будут убывать члены знакопеременного (из-за cos _n X) ряда (4.5) с увеличением номера n. Исследования показали, что уже при Fo ряд (4.5) становится настолько быстросходящимся, что распределение температуры достаточно точно, с ошибкой не более 1 %, описывается первым членом ряда (4.5)

(4.7)

Как видно из (4.7), при фиксированной безразмерной координате Х натуральный логарифм безразмерной температуры  линейно зависит от безразмерного времени Fo. Для Х=0 и Х=1 решение (4.7) в [1] представлено в виде номограмм для различных значений чисел Био, так как ₁ зависит в соответствии с (4.6) только от числа Био. Эти номограммы можно использовать в практических расчетах.

При Bi  (практически при Bi 100) из (4.6) имеем ctg =0 и _{n ,} где n=1, 2, …… В этом случае температура поверхности пластины сразу при Fo0 становится равной температуре окружающей среды, а безразмерная температура  при Х=1 =0. Иначе говоря, процесс отвода теплоты с поверхности тела происходит существенно интенсивнее, чем выравнивание температуры в теле. В этом случае процесс охлаждения (нагревания) определяется размерами тела и его физическими свойствами.

При Bi 0 (практически при Bi  0,1) ctg = и _n =(n-1). В этом случае все члены ряда (4.5), кроме первого, равны нулю. Но при ₁ 0

.

С другой стороны, при ₁ 0 .

Учитывая это, уравнение (4.5) можно переписать в виде

(4.8)

При малых числах Bi значение и температура на поверхности пластины мало отличается от температуры в центре. Это указывает на то, что температура по толщине пластины практически распределяется равномерно. Иначе говоря, процесс выравнивания температуры в теле происходит существенно интенсивнее, чем отвод теплоты с поверхности тела, и задача охлаждения (нагревания) становится внешней.

Количество отданной (полученной) стенкой теплоты на любой момент времени ₁ можно определить из следующих соображений. Количество отданной (полученной) стенкой теплоты с обеих ее поверхностей за время от =0 до = должно равняться (в изобарном процессе) изменению энтальпии пластины за период ее полного охлаждения (нагревания)

, (4.9)

где с – удельная теплоемкость;

f – площадь боковой поверхности;

 – плотность.

Тогда за любой промежуток времени от =0 до =_1., или, что то же, от Fo=0 до Fo= Fo₁, энтальпия пластины изменится на

или

(4.10)

где средняя безразмерная температура по толщине пластины в момент времени ₁.

Из соотношений (4.9) и (4.10) следует, что расчет количества теплоты, отданного (полученного) пластиной, сводится к нахождению средней безраз-мерной температуры в интересующий нас момент времени. Средняя безраз-мерная температура для слоя пластины от ее центра до плоскости Х равна

в соответствии с теоремой о среднем.

Если в это выражение подставим под знак интеграла значение  из уравнения (4.5) и проинтегрируем в пределах от нуля до единицы, то получим

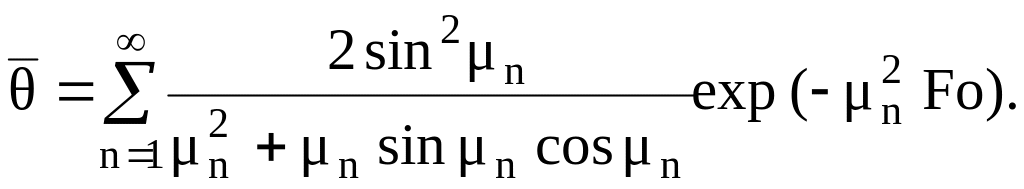(4.11)

Подставив в уравнение (4.10) вычисленное по формуле (4.11) значение средней температуры пластины для интересующего нас момента времени Fo, получим количество теплоты, отданное пластиной в окружающую среду за этот промежуток времени.