3.9. Теплопередача через ребристую стенку

Наличие ребер на стенке увеличивает поверхность ее соприкосновения с теплоносителем и тем самым уменьшает термическое сопротивление теплопередаче. Поэтому наличие ребер может использоваться как средство интенсификации процесса теплопередачи или как средство снижения температуры стенки. Пусть на рис. 3.2 поверхность стенки со стороны жидкости с температурой Т_ж2 имеет в наличии ребра. При Т_ж1Т_ж2 температура ребра, равная у его основания температуре поверхности между ребрами Т_с2, будет уменьшаться к его концу. Температуру среды Т_ж2 можно считать неизменной для всей поверхности ребра. Поэтому участки поверхности ребра, удаленные от основания, будут отдавать меньше тепла, чем участки, расположенные вблизи основания ребра. Отношение количества тепла, передаваемого поверхностью ребер в окружающую среду Q_p, к теплу, которое эта поверхность могла бы передать при постоянной температуре на поверхности ребер, равной температуре у их основания, Q_p, называется коэффициентом эффективности ребер

.

Коэффициент эффективности ребер всегда меньше единицы. Чем резче меняется температура вдоль ребра, тем меньше коэффициент эффективности. Для коротких ребер, выполненных из высокотеплопроводных материалов, коэффициент эффективности близок к единице. Определим тепловой поток через плоскую стенку, площадь гладкой поверхности которой F₁, а площадь ребристой поверхности – F₂. Площадь F₂ складывается из площади боковой поверхности ребер F_p и площади межреберных участков F_м. При стационарном режиме поток тепла от горячей среды к стенке, через стенку и от стенки к холодной среде выразится формулами

F₁ (3.63)

(3.64)

(3.65)

Так как

,

то, подставив это в (3.65) и исключив из (3.63), (3.64) и (3.65) температуры Т_с1 и Т_с2, получим

. (3.66)

Если проанализировать эту формулу при , то можно обнаружить, что для интенсификации теплообмена стенку необходимо оребрять со стороны малого коэффициента теплоотдачи. Если ребра используются как средство снижения температуры стенки, то независимо от коэффициентов теплоотдачи их постановка должна выполняться со стороны холодного теплоносителя. Увеличение поверхности ребристой стенки приводит к уменьшению термического сопротивления теплоотдаче, но при этом возникает дополнительное термическое сопротивление теплопроводности ребер. Поэтому при небольшом коэффициенте теплопроводности материала постановка ребер на поверхности стенки будет мало эффективной или даже вызовет уменьшение эффективности теплообмена. Анализ переноса тепла в ребре показывает, что ребра уменьшат термическое сопротивление теплоотдаче при условии , где  – толщина ребра.

3.10. Температурное поле и коэффициент эффективности ребра постоянного поперечного сечения

Рассмотрим на рис. 3.5 ребро постоянного поперечного сечения, для которого изменением температуры по поперечному сечению ребра можно пренебречь по сравнению с изменениями температуры по длине ребра.

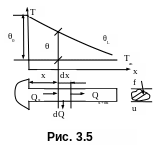
К

Рис. 3.5

оэффициент теплоотдачи  и температура окружающей среды Т_ж постоянны для всей поверхности ребра. Площадь поперечного сечения ребра f, периметр сечения u, длина ребра и коэффициент теплопроводности материала  также постоянны. При стационарном тепловом режиме поток тепла Q_x, подводимый в сечении ребра х частично теплопроводностью передается вдоль ребра Q_x+dx частично рассеивается в окружающую среду dQ.

. (а)

Вводя избыточную температуру =T-T_ж, согласно закону Фурье имеем

(б)

(в)

Но по закону Ньютона-Рихмана

. (г)

Подставив соотношения (б), (в) и (г) в формулу (а), получим

, (3.67)

где .

Решением дифференциального уравнения (3.67) является функция

. (3.68)

Константы интегрирования С₁ и С₂ можно определить из граничных условий:

при х=0; =₀,

x=; ,

где _l, – избыточная температура и коэффициент теплоотдачи на торце ребра.

На торце ребра избыточная температура минимальна, и поверхность его часто меньше боковой поверхности ребра. Поэтому теплообменом с торца ребра часто можно пренебречь. В этом случае второе граничное условие запишется в виде

при x=;

Определим константы интегрирования, пренебрегая теплоотдачей с торца ребра. Подстановка граничных условий в уравнение (3.68) дает

Из совместного решения этих уравнений определяются С₁ и С₂

Гиперболический косинус выражается формулой

Подставив С₁ и С₂ в формулу (3.68), получим уравнение для температурного поля в ребре

. (3.69)

Избыточная температура на конце ребра при x = равна

Весь рассеиваемый ребром поток тепла проходит путем теплопроводности через сечение его основания. Поэтому

Продифференцировав (3.69) и подставив в эту формулу, получим

(3.70)

Эта формула не учитывает теплоотдачу торца ребра. Если принять, что коэффициент теплоотдачи на торце ребра такой же, как на его боковой поверхности, то теплоотдачу торца ребра можно учесть удлинением ребра на величину f/u и вместо длины ребра  в расчетах использовать эффективную длину _эф=+f/u. Тогда коэффициент эффективности ребра постоянного по длине произвольного поперечного сечения равен

(3.71)