3.7. Критический диаметр тепловой изоляции труб

Рассмотрим влияние изменения наружного диаметра многослойной цилиндрической стенки на примере двухслойной стенки на линейное термическое сопротивление теплопередаче. Выражение в знаменателе (3.45),представляющее линейное термическое сопротивление теплопередаче, для этого случая будет иметь вид

Выясним, как будет изменяться R_L при изменении толщины изоляции или тоже наружного диаметра d₃. Для этого продифференцируем R_L по d₃ и приравняем производную нулю

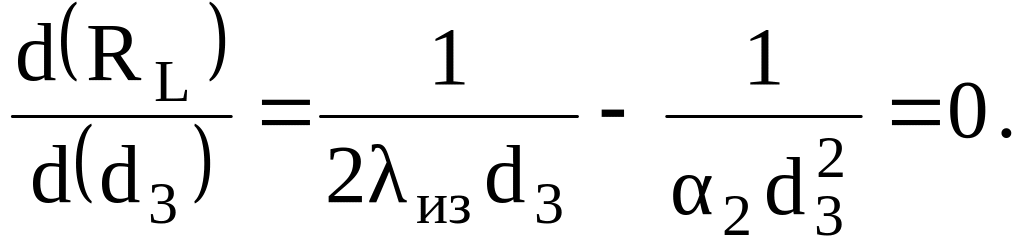
Значение d₃=2_из/₂ из этого выражения соответствует экстремальной точке кривой R_L=f (d₃). Исследовав эту кривую любым из известных способов, например, взяв вторую производную и подставив экстремальное значение d₃, получим

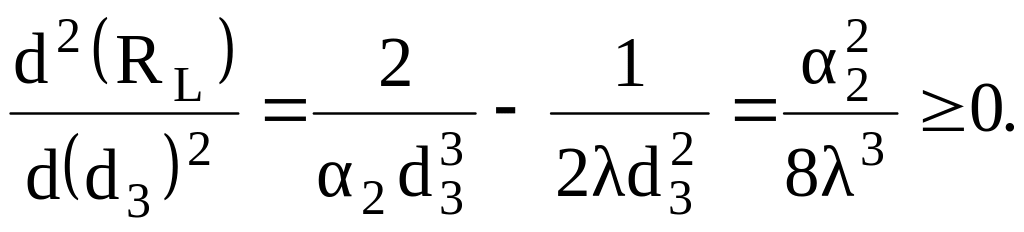
Так как вторая производная положительная, то при значении диаметра d₃=2_из/₂ линейное термическое сопротивление теплопередаче будет мини-мальным. Значение внешнего диаметра изоляции, соответствующего мини-мальному линейному термическому сопротивлению теплопередаче, называется критическим диаметром тепловой изоляции и рассчитывается по формуле

(3.47)

Разумеется, понятие критический диаметр имеет место и для однослойной цилиндрической стенки. Для плоской стенки любой дополнительный слой из любого материала при прочих равных условиях приводит к возрастанию термического сопротивления теплопередаче и уменьшению потока тепла через стенку. Причина этого в том, что поверхности у плоской стенки одинаковы. Для цилиндрической стенки с ростом наружного диаметра увеличивается линейное термическое сопротивление теплопроводности и одновременно уменьшается линейное термическое сопротивление теплоотдачи. Поэтому при увеличении внешнего диаметра изоляции линейная плотность теплового потока сначала будет возрастать и при d₃ = d_кр будет иметь максимум. При дальнейшем увеличении d₃ линейная плотность теплового потока будет уменьшаться. Выбрав какой-либо теплоизоляционный материал для покрытия трубы, прежде нужно рассчитать критический диаметр изоляции по формуле (3.47). Для эффективной работы тепловой изоляции необходимо, чтобы d_кр d₂. В противном случае при увеличении толщины изоляции q_L возрастает в диапазоне от d₂ до d_кр., а при d₃ d_кр – уменьшается. Следовательно, некоторый слой тепловой изоляции не будет оправдывать своего назначения. Понятие «критический диаметр изоляции» используют не только при изоляции цилиндрической стенки, но и любой стенки, у которой внутренняя поверхность не равна наружной поверхности.

3.8. Теплопередача и теплопроводность тел с внутренними источниками тепла

Рассмотрим температурное поле в телах простейшей формы при объемном тепловыделении, т.е. для случая, когда внутренние источники тепла равномерно распределены по всему объему тела.

Пусть имеем неограниченную плоскую стенку толщиной 2, внутри которой действуют внутренние источники тепла плотностью q_V. Стенка находится в жидкости с температурой Т_ж. На обеих поверхностях стенки коэффициент теплоотдачи  одинаков. Так как стенка охлаждается симметрично, то выберем начало координат на оси симметрии стенки. Тогда в начале координат будет максимальная температура, а градиент температуры равен нулю. Необходимо определить поле температур в пластине и количество тепла, отданное в окружающую жидкость.

Дифференциальное уравнение (3.1) в данном случае упрощается и принимает вид

. (3.48)

Будем рассматривать лишь правую половину пластины, поскольку поле температуры симметрично относительно плоскости х=0. Тогда граничные условия имеют вид

(3.49)

После интегрирования (3.48) получим:

(3.50)

(3.51)

Постоянные интегрирования С₁ и С₂ найдем из граничных условий (3.49). При х=0 из уравнения (3.50) получаем С₁=0. Подставив уравнения (3.50) и (3.51) в (3.49) при х=, получим

.

Откуда имеем

.

Подставив значения постоянных С₁ и С₂ в выражение (3.51), получим уравнение температурного поля

(3.52)

Из соотношения (3.50) имеем, что плотность теплового потока изменяется по толщине стенки линейно

Плотность теплового потока на поверхности пластины равна

(3.53)

Общий поток тепла, отданный обеими поверхностями стенки, составит

Если в уравнении (3.52) положить , то граничные условия третьего рода вырождаются в граничные условия первого рода, ибо при  получим Т_ж=Т_с. Тогда из уравнения (3.52) имеем

(3.54)

Из уравнений (3.52) и (3.54) можно определить максимальную температуру в центре пластины при х=0.

Для цилиндра, как и для пластины, задача одномерна и симметрична. Уравнение (3.48) при этом имеет вид

(3.55)

Граничные условия:

при ,

при (3.56)

После интегрирования (3.55), используя подстановку dT/dr=u, получим

(3.57)

(3.58)

Постоянные С₁ и С₂ определяются из граничных условий (3.56). После их подстановки в (3.57) и (3.58) получим окончательно

(3.59)

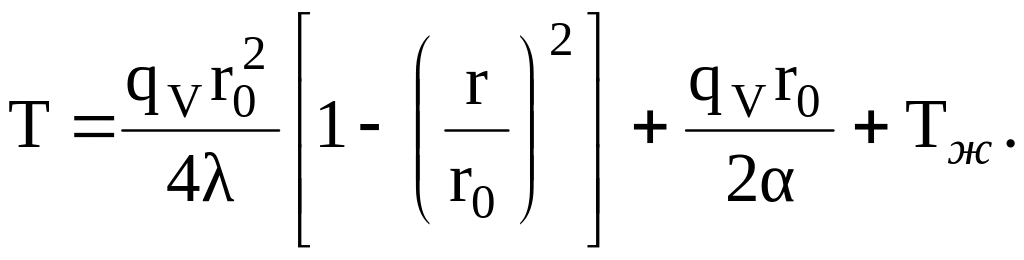(3.60)

На поверхности цилиндра плотность теплового потока и поток тепла соответственно равны

, (3.61)

(3.62)

Если в полученных решениях полагать =, то граничные условия третьего рода вырождаются в граничные условия первого рода Т_ж=Т_с, и из (3.60) получим выражение для поля температуры.