Преобразования напряжения в частоту (плюс счетчик импульсов за фиксир. Δt)

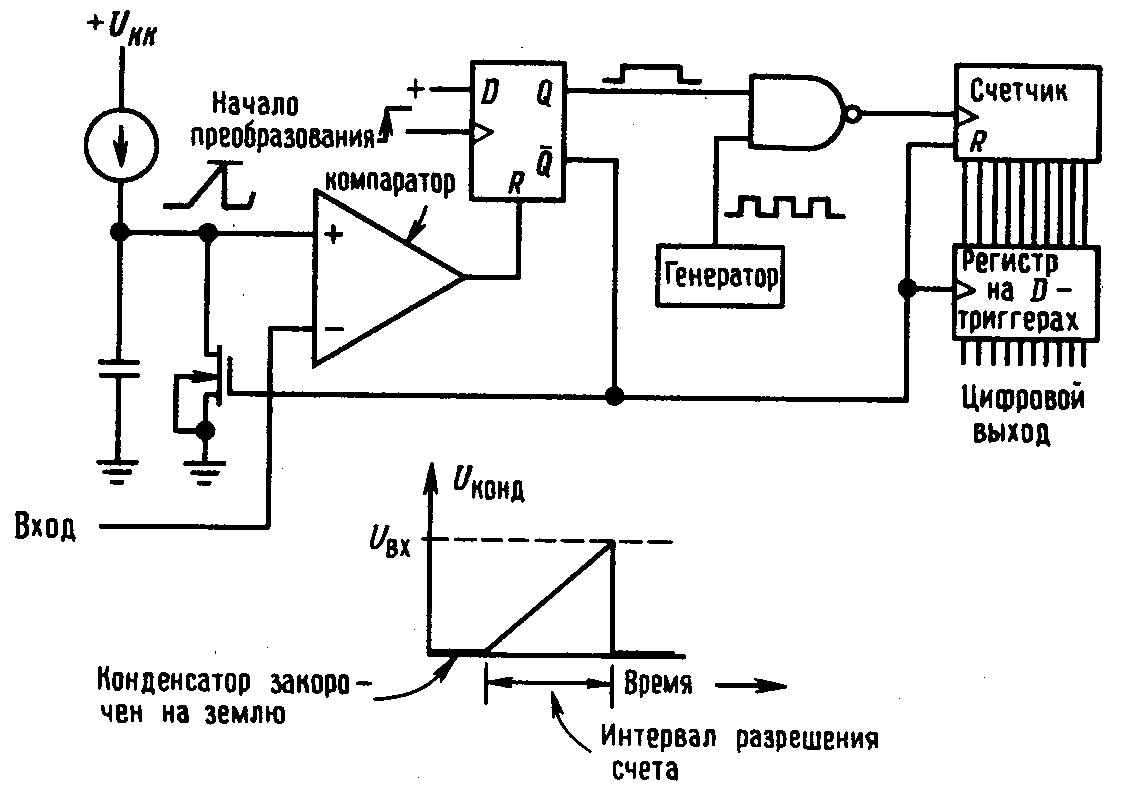
АЦП с одностадийным интегрированием

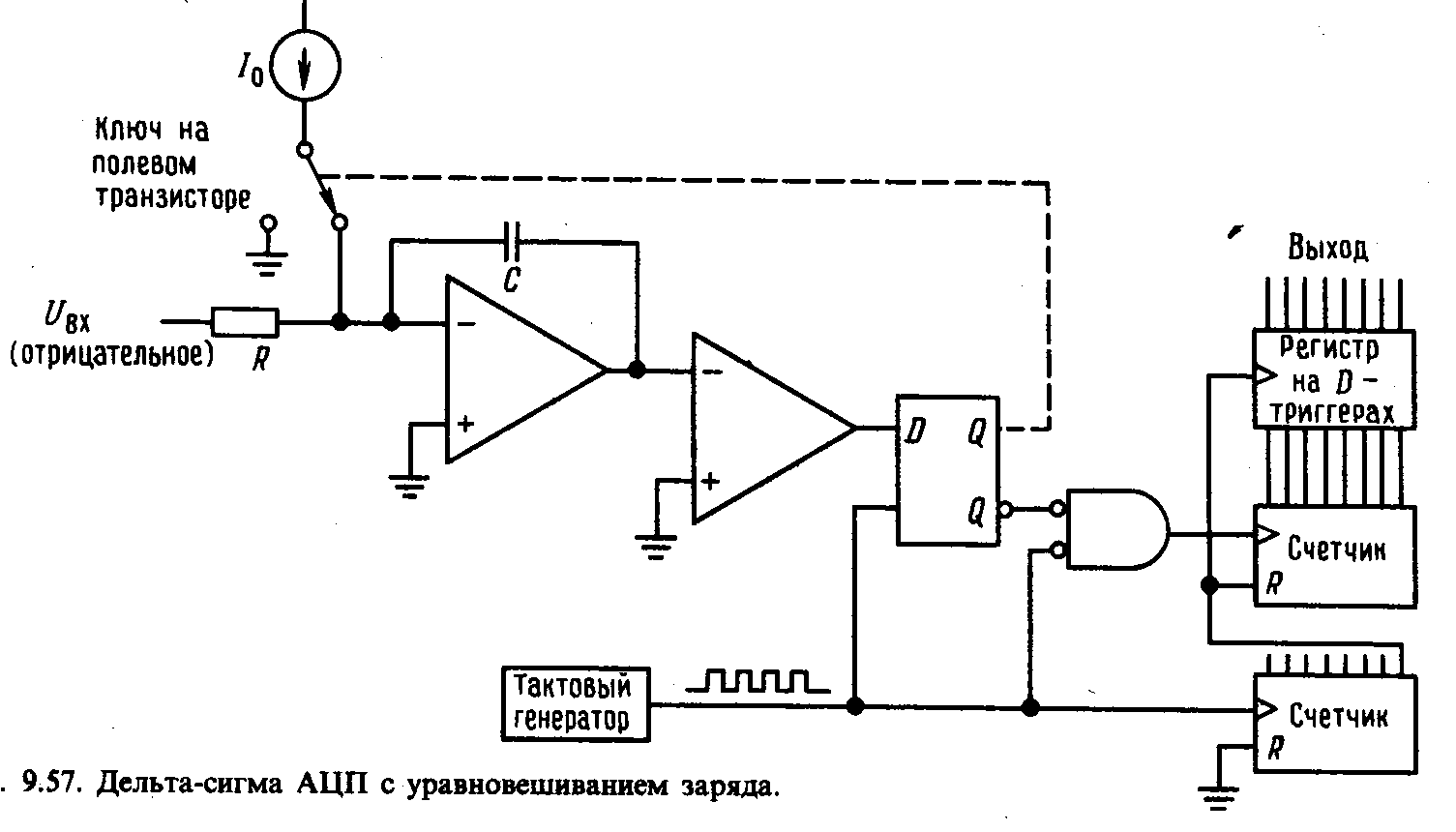
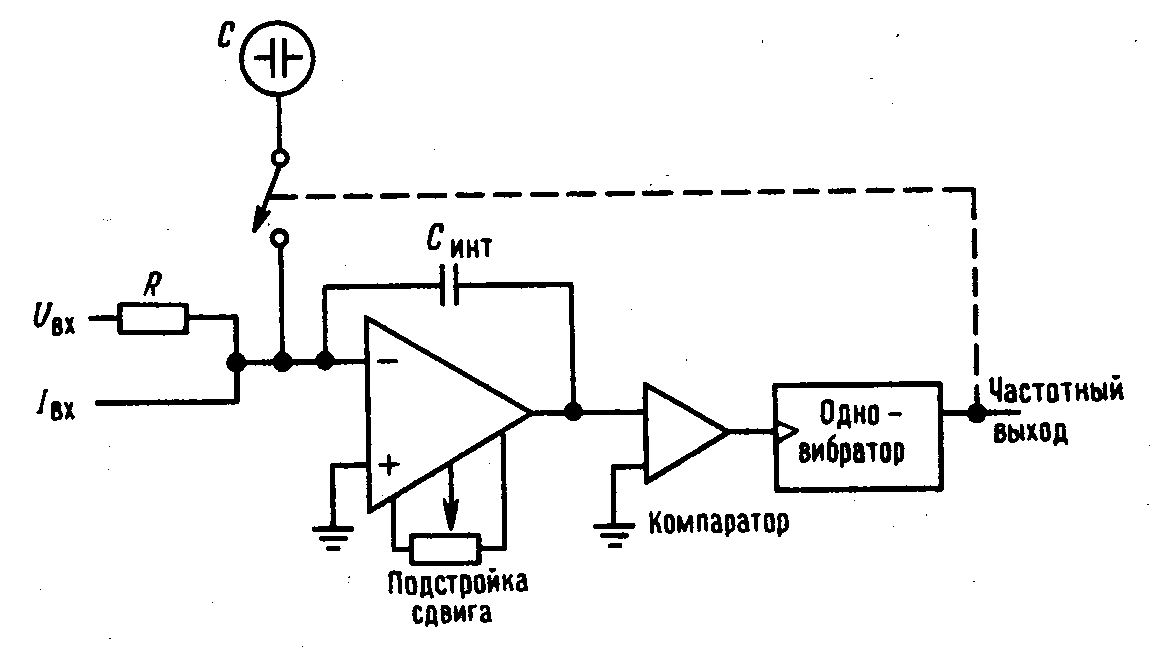
Преобразователь напряжения в частоту с уравновешиванием заряда

Резонанс в нелинейном колебательном контуре

Где ,

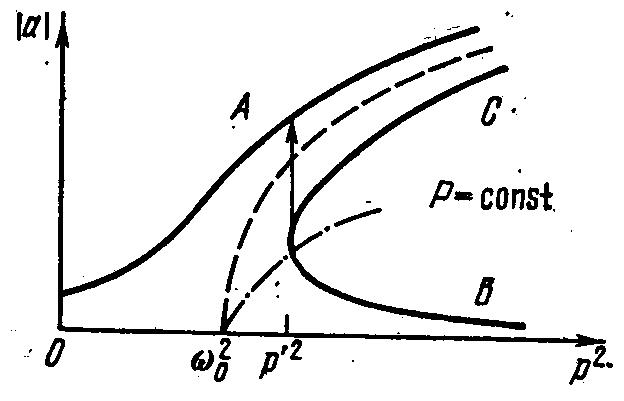
Резонанс в нелиейном контуре без потерь

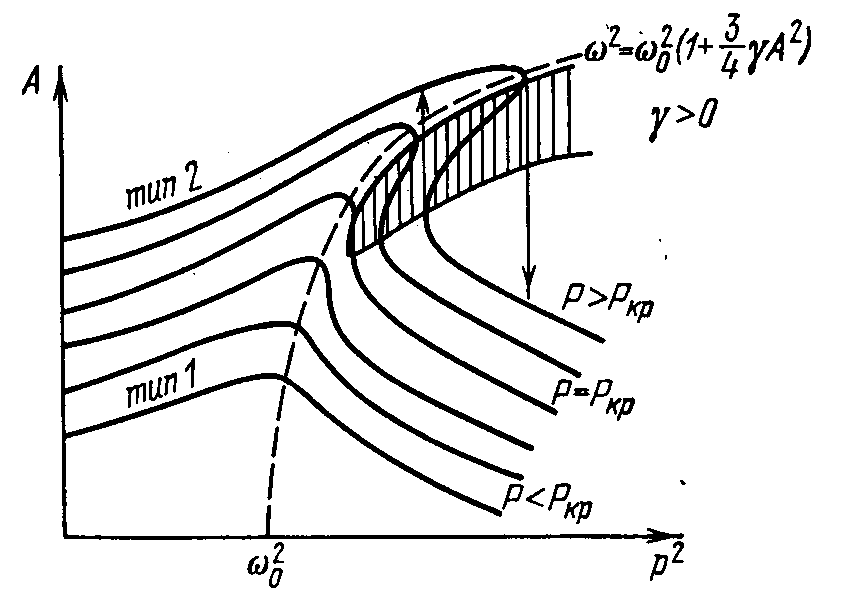
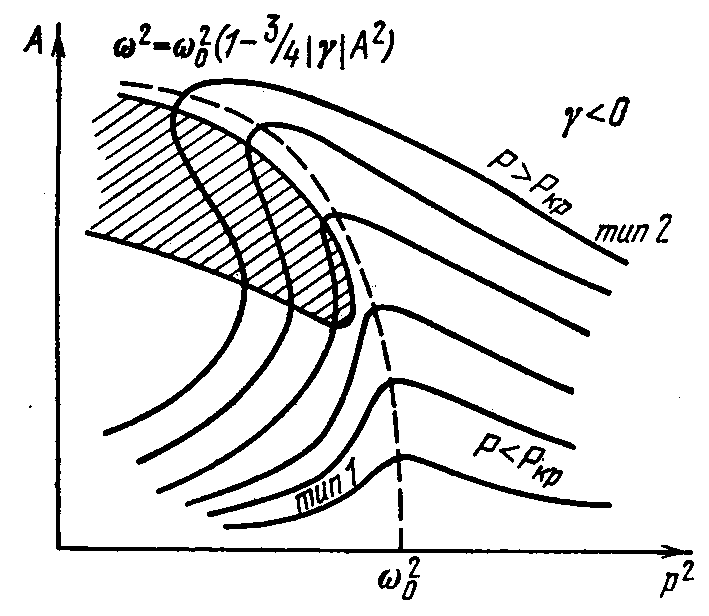
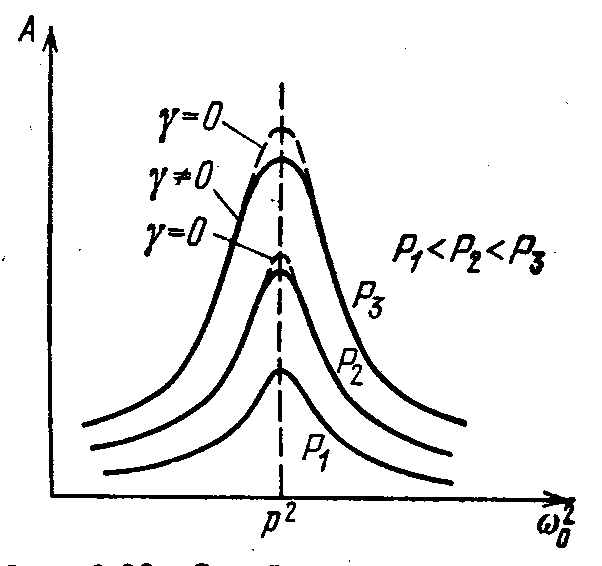
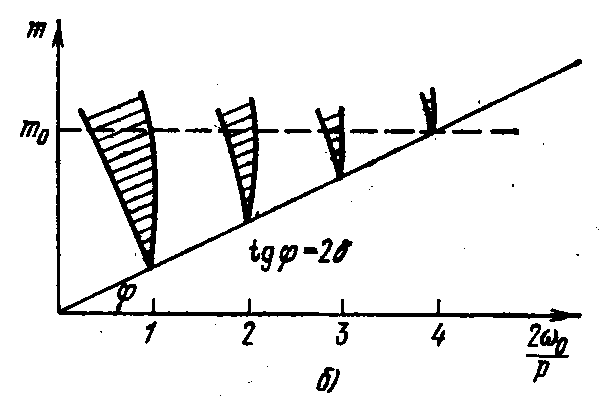
Параметрические колебательные системы

Уравнение Хилла → Уравнение Матье

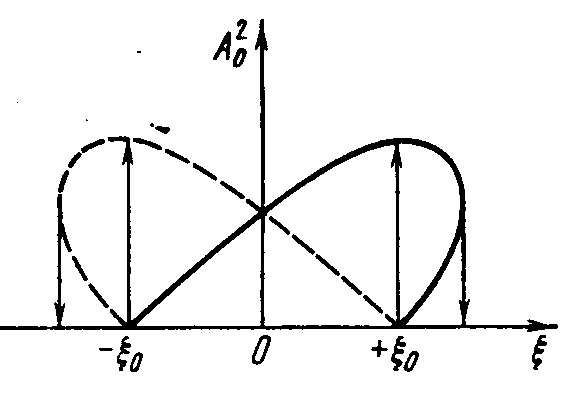
А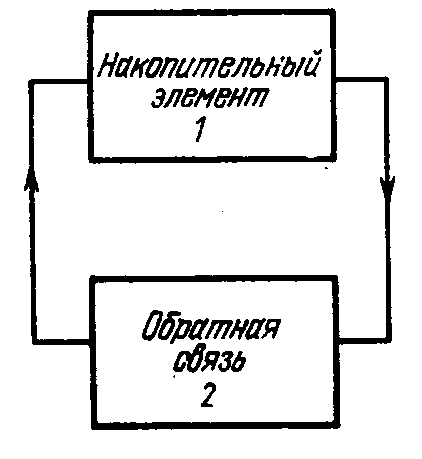 втоколебательные системы

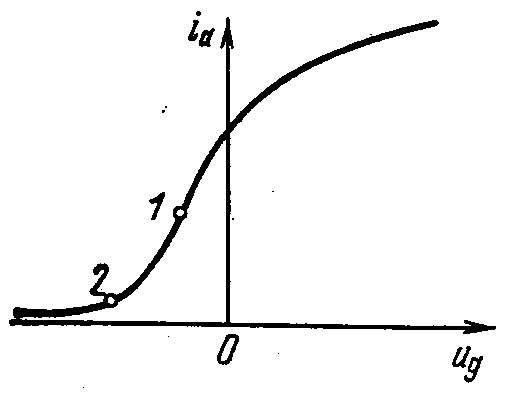
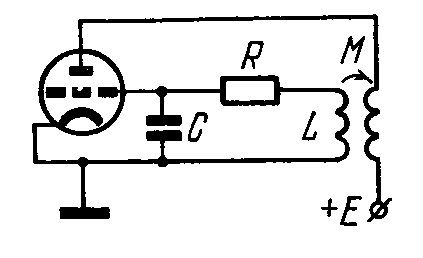
Характеристика триода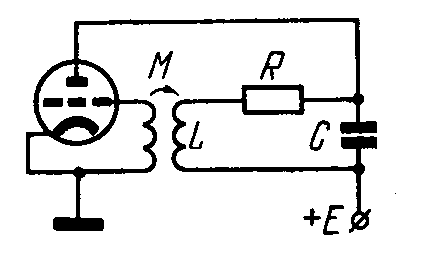

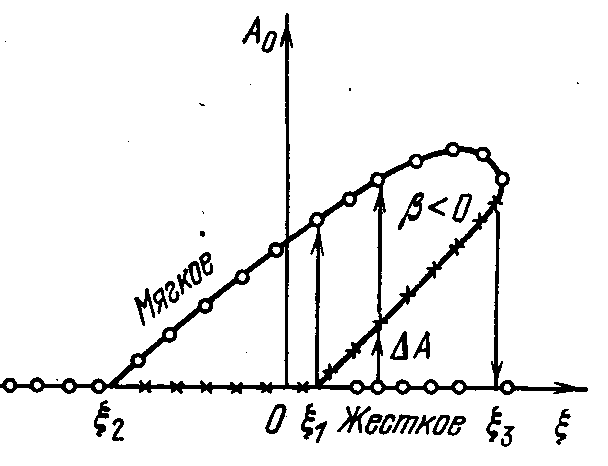
Мягкий и жесткий режимы возбуждения автоколебаний

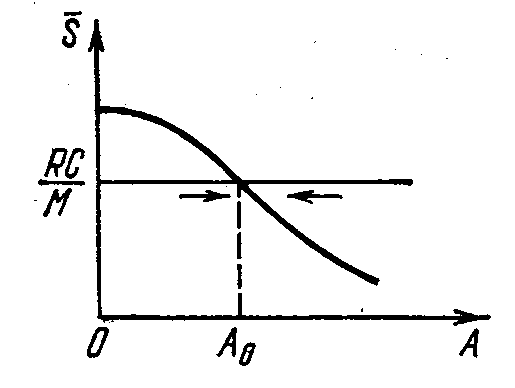
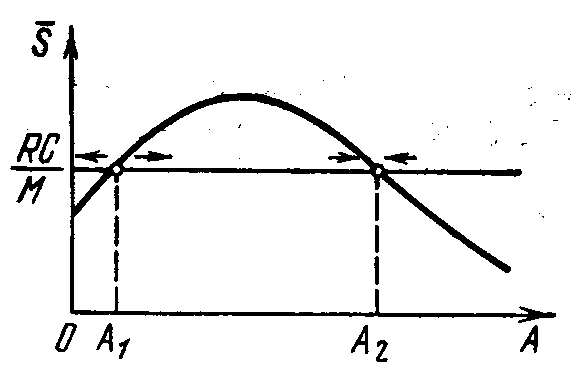
Синхронизация внешним сигналом

• Увлечение частоты

• Подавление собственных колебаний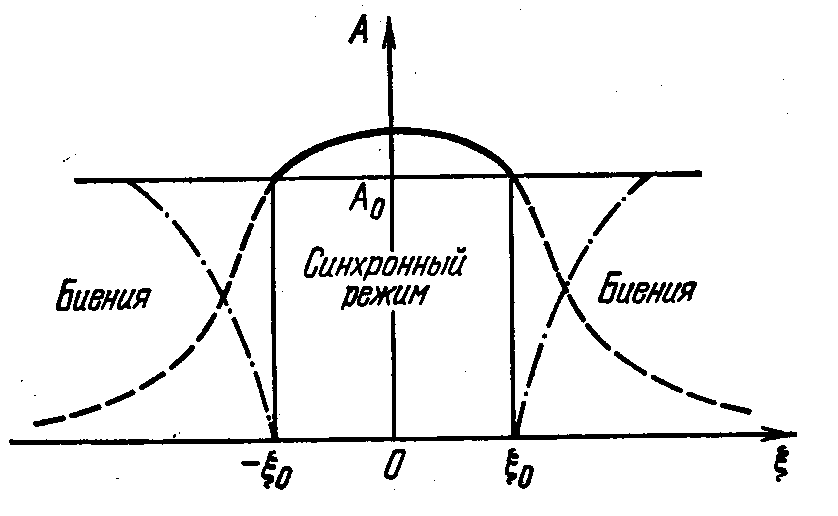

Взаимная синхронизация двух генераторов

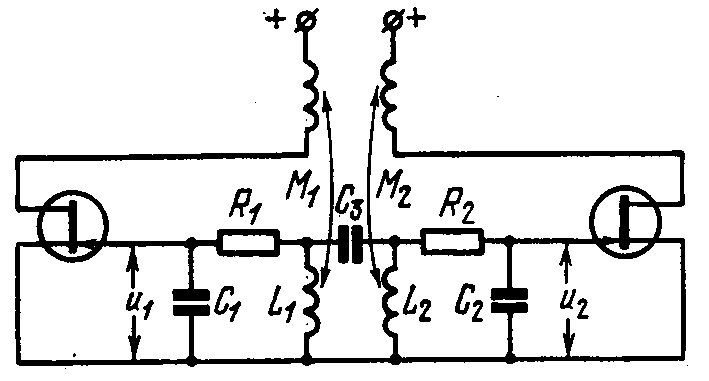
Автоколебательные системы с запаздывающей обратной связью

Графики зависимости амплитуды и частоты генерации от величины запаздывания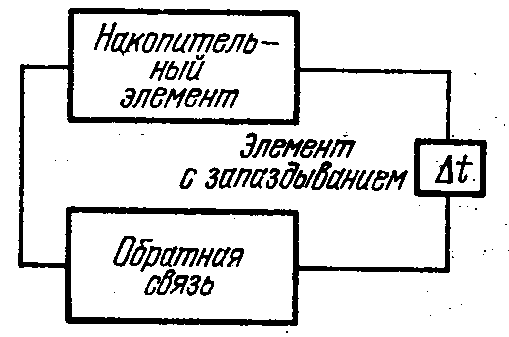

Генератор без накопит. цепи

Последовательное прохождение импульсов через усилитель с задержкой

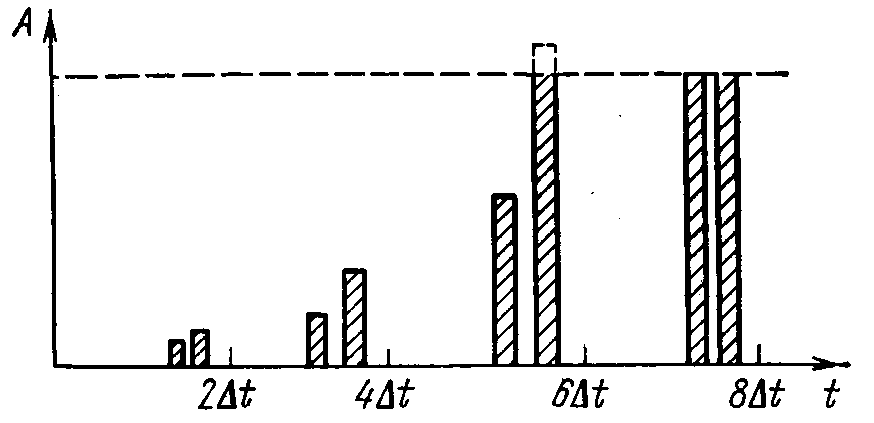
Интеграл Дюамеля для описания лин. системы:

где - функция отклика на единичный скачок напряжения, которая в отсутствие дисперсии дает чистый сдвиг во времени

,

где - функция потерь и других параметров.

,

- итерационная задача для системы без дисперсии

Построение (диаграмма) Ломерея:

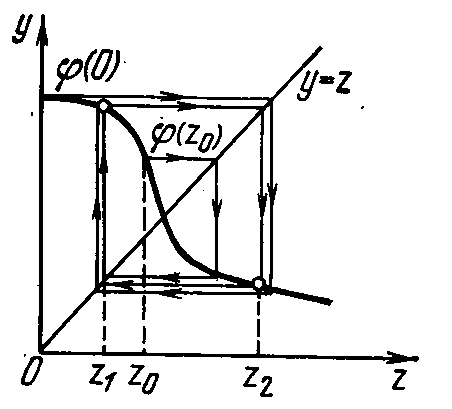
В линейной системе с дисперсией запаздывания

(возбуждение колебаний):

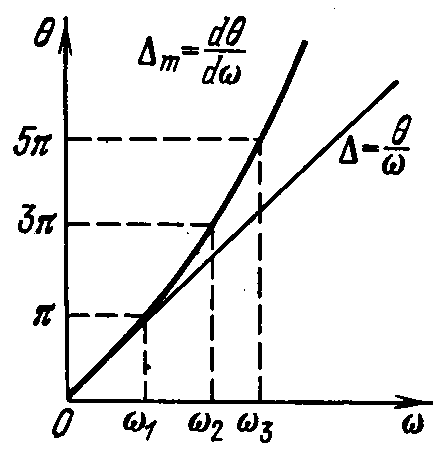- экспоненц. функции времени, которые возрастают, если коэффициент передачи системы К > 1.

Установление стационарного режима колебаний определяется нелинейными свойствами системы при больших амплитудах осцилляций. В естественных условиях устанавливается периодический режим осцилляций с низшей частотой из спектра возбуждения.

Колебания в линейных системах с двумя степенями свободы

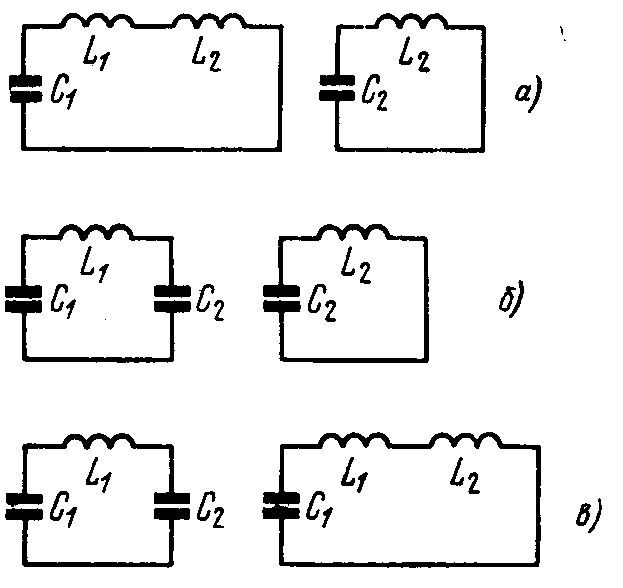
Системы с одной степенью свободы, на которые можно разбить сложную колебательную систему, называются парциальными. Частоты свободных колебаний отдельных парциальных систем называются парциальными частотами полной системы

Положив в первом уравнении и - во 2-м уравнении, получаем парциальные частоты:

, .

Если ввести коэффициенты связи , , то получаем систему:

, решение которой ищем в виде: .

Подставляя эти решения в исходные уравнения, получаем систему двух линейных уравнений для нахождения амплитуд А и В. Приравнивая к нулю детерминант этой линейной системы, получаем уравнение для определения частоты:

,

решение которого дает две собственные или нормальные частоты системы: .

,

где коэффициенты распределения амплитуд:

Связанность маятников: .

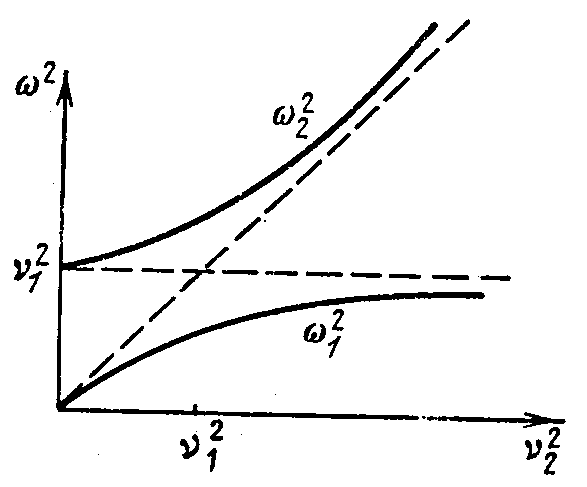
График Вина для собственных частот Зависимость коэф. распределения амплитуд

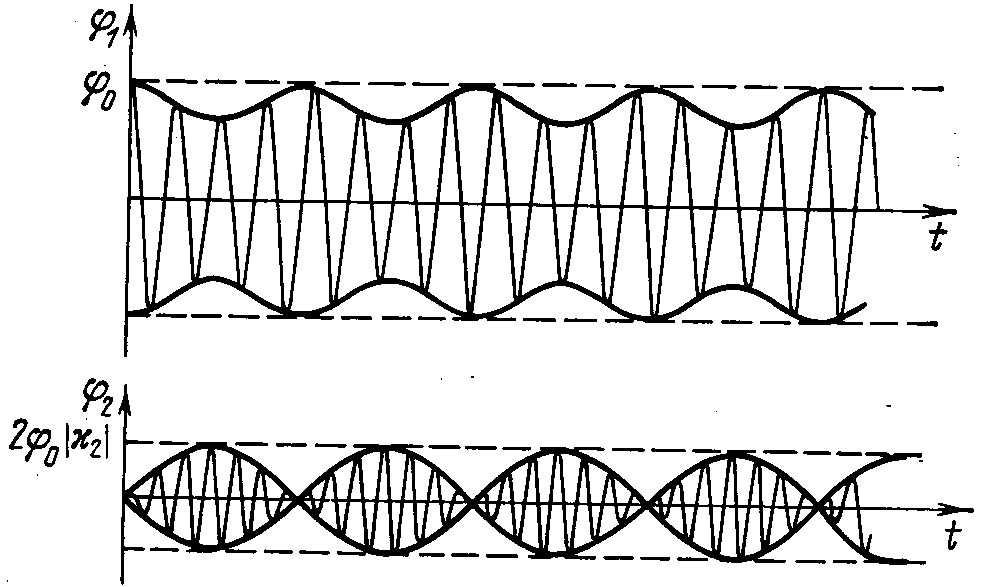
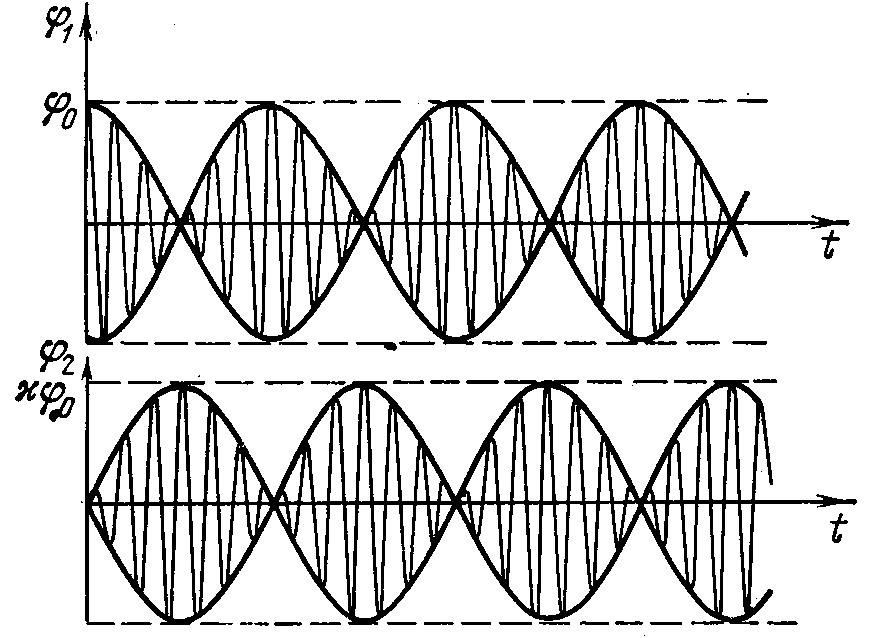
Колебания связанных маятников при слабой и сильной связанности

Вынужденные колебания в системах с двумя степенями свободы

Коэф. связи меньше (1), близок (2) и больше (3) критического значения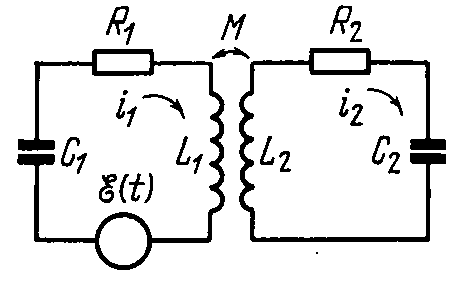

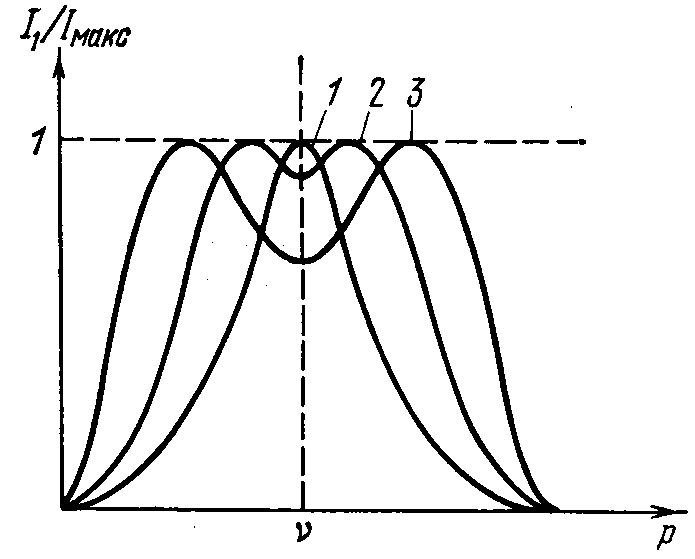
Резонанс. кривая

( 1) Принцип взаимности для лин. систем:

Ампл. вын. колеб. во 2-м контуре при включении ЭДС в 1-й контур равна ампл. вын. колеб. в 1-м контуре при включении ЭДС во 2-й контур.

(2) при определенном соотношении амплитуд внешних ЭДС в системе может отсутствовать резонанс (на частоте ω₁ или ω₂).

Автоколебательная система с дополнительным контуром

(с 2-мя степенями свободы)

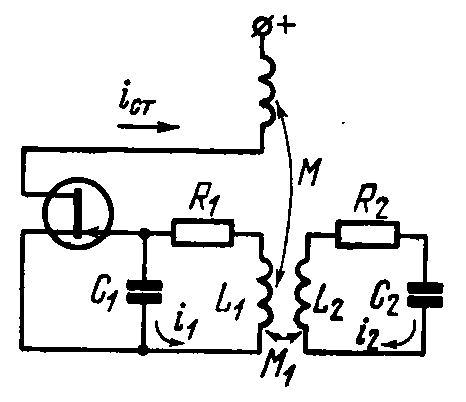
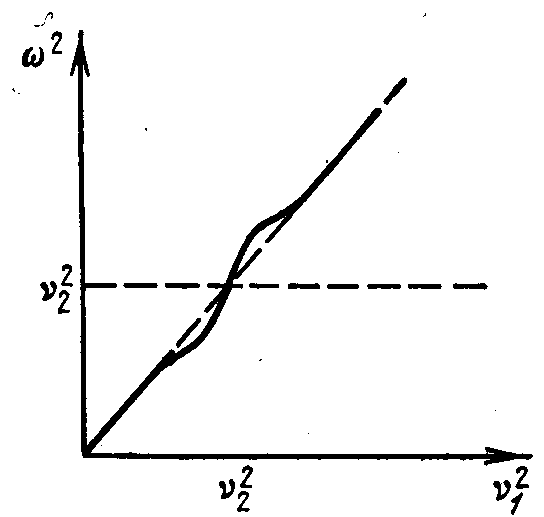
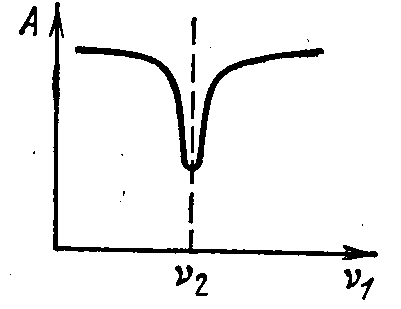
Зависимость генерируемой частоты и амплитуды колебаний в первом контуре (отсос энергии) от парциальной частоты первого контура при слабой связи контуров.

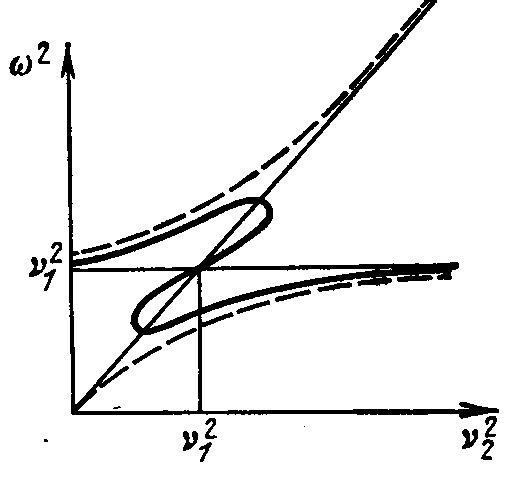
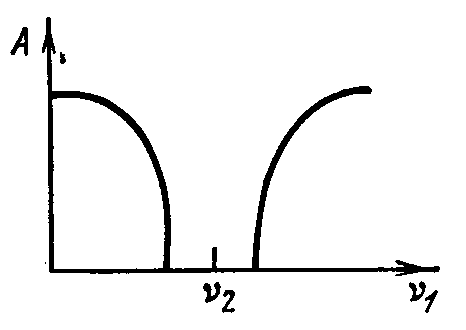
Зависимость генерируемой частоты от парциальных частот первого и второго контуров при сильной связи, а также амплитуда колебаний в первом контуре вблизи области гашения колебаний в первом контуре.

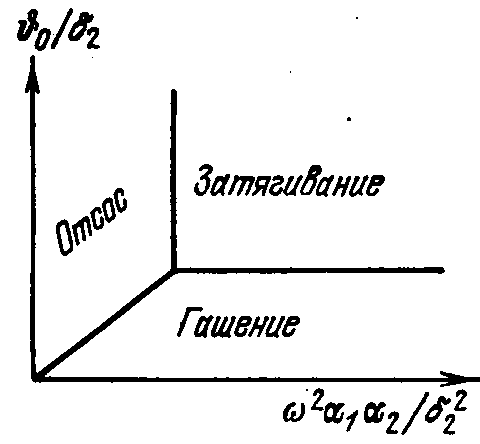
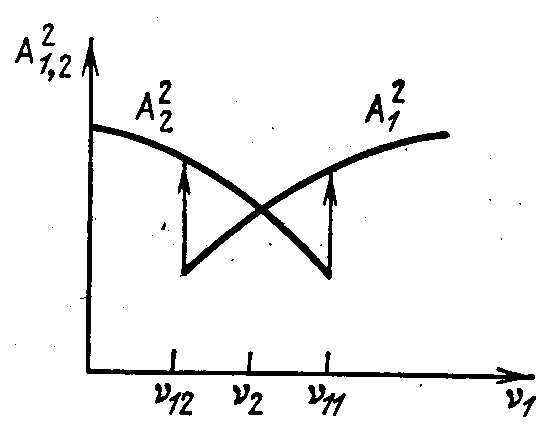
Области различного поведения системы Явление затягивания частоты генерации

Параметрические системы с n степенями свободы

Соотношения Мэнли – Роу (опубл. В 1956 г.)

(для реактивного нелинейного элемента без потерь)

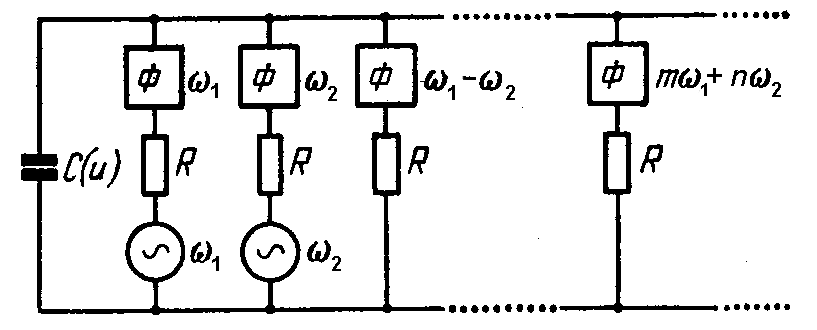
Воздействуют две ЭДС с несоизмеримыми частотами ω₁ (сигнал) и ω₂ (накачка), C(U) – нелинейная емкость, Ф – идеальные узкополосные фильтры, R – сопротивления.

На каждом активном элементе R выделяется мощность P_mn на частоте (mω₁ + nω₂).

Закон сохранения энергии для рассматриваемой системы:

,

из которого вытекают энергетические соотношения Мэнли – Роу:

, (a)

. (б)

Вывод соотношений Мэнли-Роу. Введем обозначение комбинационной частоты ω_mn = mω₁ + nω₂ , где m и n – положительные и отрицательные целые числа.

, , ,

Здесь - действительные числа, - комплексные числа, причем , , ,

Средняя мощность, поступающая в конденсатор на частотах равна

Условие отсутствия потерь в нелинейном конденсаторе позволяет записать равенство

,

которое переписываем в виде ,

или: .

Можно показать, что двойные суммы по отдельности рану нулю. Для этого можно рассмотреть большое число систем, изображенных на исходном рисунке, Потребуем, чтобы у всех систем ω₁ и ω₂  были различны, а нелинейные конденсаторы и коэффициенты U_mn , Q_mn , I_mn  были бы одинаковыми. Это можно сделать за счет изменения внешних сопротивлений и генераторов (ω₁ и ω₂ ). Тогда и отношения будут одинаковыми для всех систем и не будут зависеть от ω₁ и ω₂ . Это рассуждение приводит к соотношениям Мэнли-Роу (а) и (б), которые справедливы для стационарных и квази-стационарных процессов.

Пример 1. Параметрическая система с нагрузкой на одной единственной комбинационной частоте , - сигнал, - накачка.

, . → .

Э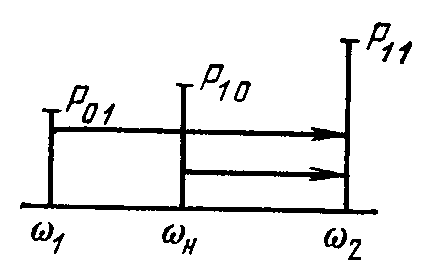 то означает, что система устойчива, нет самовозбуждения. Коэфф. усиления (максим.) по мощности (усилитель с преобразованием частоты):

Пример 2. То же самое, но с нагрузкой на частоте

.

, , .

Схема потенциально неустойчива, т.к. энергия поступает в нагрузку независимо от наличия энергии сигнала на частоте . Схема представляет собой регенеративный усилитель (часть энергии генератора накачки идет в дополнительный контур, а остальная часть в цепь сигнала), склонный к самовозбуждению.

П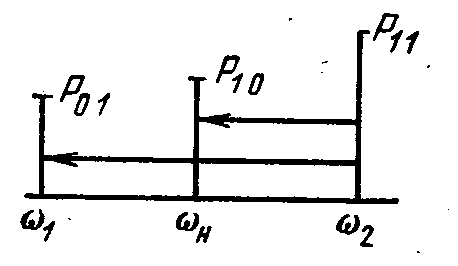 ример 3. Последняя схема, используемая как вчдемодулятор. Входной сигнал – модулированный сигнал с комбинационной частотой , накачка – с частотой . Энергия модулированного сигнала частично идет в первый контур, а частично – в цепь генератора накачки. В контуре выделяется продетектированный сигнал частоты , причем его мощность меньше мощности модулированного сигнала в раз. Эта схема способна к самовозбуждению.

Метод медленно меняющихся амплитуд (метод ММА)

Уравнение: , где

Замена: , укороченные уравнения:

,

Распределенные системы

Телеграфные уравнения для двухпроводной линии

В каждом сечении линии . Рассматривая бесконечно малый элемент длины линии, обладающий индуктивностью L и емкостью С на единицу длины, для падения напряжения на этом участке можно записать выражение: . Уменьшение тока на длине равно тому току, который ответвляется в распределенную емкость, поэтому можно записать следующее соотношение: . Это дает два так называемых телеграфных уравнения: , ,

из которых легко получаем волновые уравнения для напряжения и тока:

, , где - фазовая скорость.

Волновое сопротивление линии (импеданс) . Импеданс свободного пространства .

52