Корнев Виктор Константинович

Основы полупроводниковой электроники и теории колебаний

Литература

1. И.П. Степаненко. Основы теории транзисторов и транзисторных схем. М., Энергия, 1973.

2. П. Хорвиц, У. Хилл. Искусство схемотехники. В трех томах, пер.с англ., М., Мир, 1993.

3. В.И. Медведев, В.В. Мигулин, Е.Р. Мустель, В.Н. Парыгин. Основы теории колебаний. М., Наука, 1978.

4. Е.И. Минаев. Основы радиоэлектроники. М., Радио и связь, 1985.

5. Ю.И. Неймарк, П.С. Ланда. Стохастические и хаотические колебания. М., Наука, 1987.

Энергетические зоны твердого тела

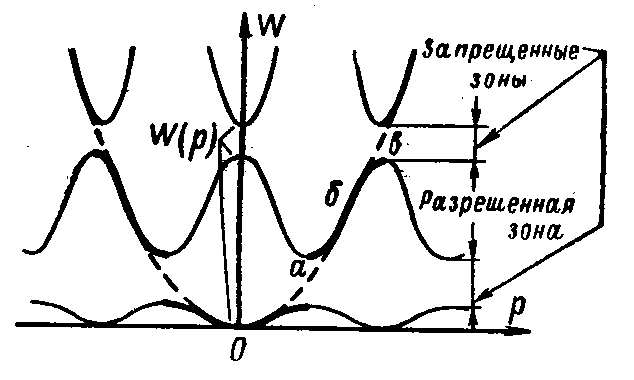
Зависимость энергии электрона от импульса p в одномерной кристаллической решетке

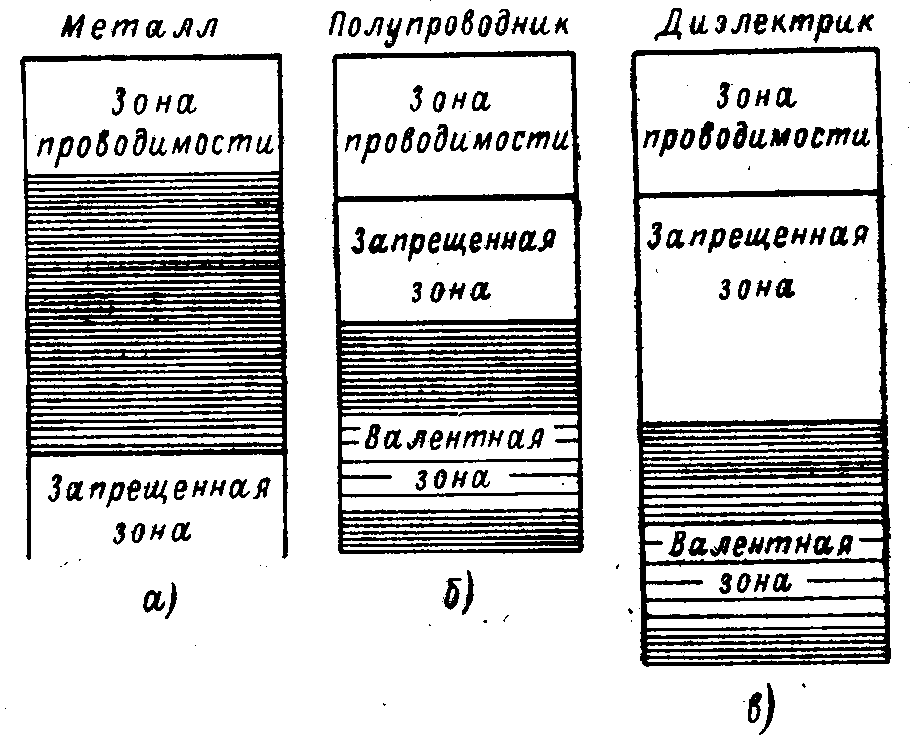
Зонная структура при Т = 0.

(а) – металл, (б) – полупроводник, (в) – диэлектрик.

Зонная структура полупроводников

Зонные структуры полупроводников:

(a) – собственный полупроводник при Т ≠ 0,

(б) – электронный полупроводник при Т = 0,

(в) – дырочный полупроводник при Т = 0.

Законы распределения носителей в зонах полупроводников

Энергетические уровни распределены по высоте разрешенной зоны неравномерно: плотность их меняется от границы в глубь зоны. Таким образом, каждому уровню с энергией W соответствует определенная плотность P(W), то есть число уровней, отнесенное к единице энергии и единице объема твердого тела. Вблизи “дна” и “потолка” каждой из разрешенных зон плотность плотность уровней P(φ) с нормированной энергией (в вольтах) φ = W/e (для узких интервалов энергии dφ) выражается следующей формулой:

где φ_b – граница зоны, m* - эффективная масса. Энергия отсчитывается от граничного уровня φ_b внутрь зоны.

Вероятность нахождения электрона на том или ином уровне дается распределением Ферми-Дирака:

“Темпер. потенциал” φ_T = kT/e ≈ T/11600, φ_T(300K) ≈ 0,025 В.

Плотность уровней энергии, функция вероятности и концентрация носителей в собственном полупроводнике.

φ_F – уровень Ферми, который в невырожденных полупроводниках всегда лежит в запрещенной зоне.

При T ≠ 0 для зон проводимости и валентной зоны (т.е. для областей энергий, достаточно отличных от энергии Ферми φ_F) распределение Ф-Д переходит в распределение Максвелла - Бльцмана (т.к. ׀φ-φ_F׀ >> φT):

 ,

Концентрация свободных электронов в зоне проводимости:

 ,

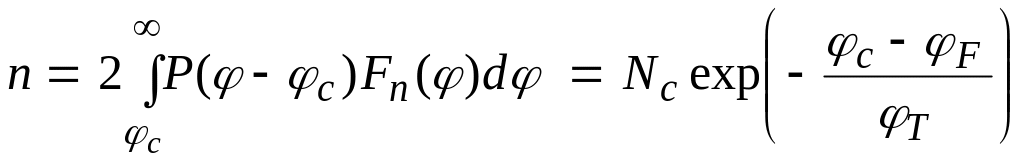где - эфф. плотность состояний (на 1 см³) в зоне проводимости. При получении этой формулы было использовано соотношение:

Концентрация свободных дырок в валентной зоне:

,

где - эфф. плотность состояний (на 1 см³) в валентной зоне.

 ,  , где

Уровень Ферми является функцией концентраций носителей.

Задача определения уровня Ферми (обр. задача) определяется интегралом:

 , (*)

где χ – хим. потенциал.

В случае электронов , , .

В случае дырок , ,.

или ,

φ_F – эл.-хим. потенциал, характеризующий и диффузию, и дрейф частиц. Поэтому в условиях равновесия φ_F = const.

1. Случай χ < 0, ׀χ׀ >> φT (невырожденные полупроводники: λ < 1).

В этом случае уравнение (*) существенно упрощается:

,

Отсюда получаем следующие выражения:

 ,

или .

2. Случай χ > 0, ׀χ׀ >> φ_T (вырожденные п/п или полуметаллы: λ > 1).

В этом случае, аппроксимируя функцию ступенчатой функцией, которая равна 1 при и равна 0 при , из уравнения (*) получаем выражение:

 .

Отсюда следует, что

;

Эти выражения справедливы при λ >> 1 (практически при λ > 3) в силу того, что рассматривается случай ׀χ׀ >> φ_T  .Полупроводники, у которых концентрация свободных носителей существенно превышает эффективную плотность состояний в разрешенной зоне, называют вырожденными или полуметаллами. Для них распределение максвелла – Больцмана недействительно и в случае сильного вырождения заменяется ступенчатой функцией: при и при . Критерии вырождения: и соответственно  .

Потенциал Ферми для вырожденных полупроводников лежит внутри соответствующей разрешено зщоны, поскольку хим. потенциалы χ_n и χ_p положительны.

Концентрация носителей.