6.Анализ чувствительности и точности сар скорости.
Анализ чувствительности САР скорости к выбору КУ.
Анализ чувствительности проводят методом сравнения 3-х схем:
Исходной
Измененный параметр +
Измененный параметр - .
Рис.20
Полученные переходные процессы приведены на Рис.21
Рис.21
Параметры переходных характеристик представлены в таблице 5.
Параметры ПХ |
Т1 |
Т1+Т1 |
Т1- Т1 |
Перерегулирование |
4 |
4,98 |
3,31 |
Время регулирования tр,с |
0.201 |
0.216 |
0.208 |
hуст,(об/мин) |
1000 |
1000 |
1000 |
Таблица 5.
7.Коррекция электромеханической следящей системы в пространстве состояний.
7.1.Структурная схема и матрично-векторное описание с доступом к переменным состояниям.
Рис.22 структурная схема электромеханической СС с доступом к переменным состояниям.
При задании команд:
>> [a,b,c,d]=linmod('v22P7')
>> h=ss(a,b,c,d)
>>step(h)
Выводится переходная характеристика аналогичная пункту 4.2.2. Рис.23
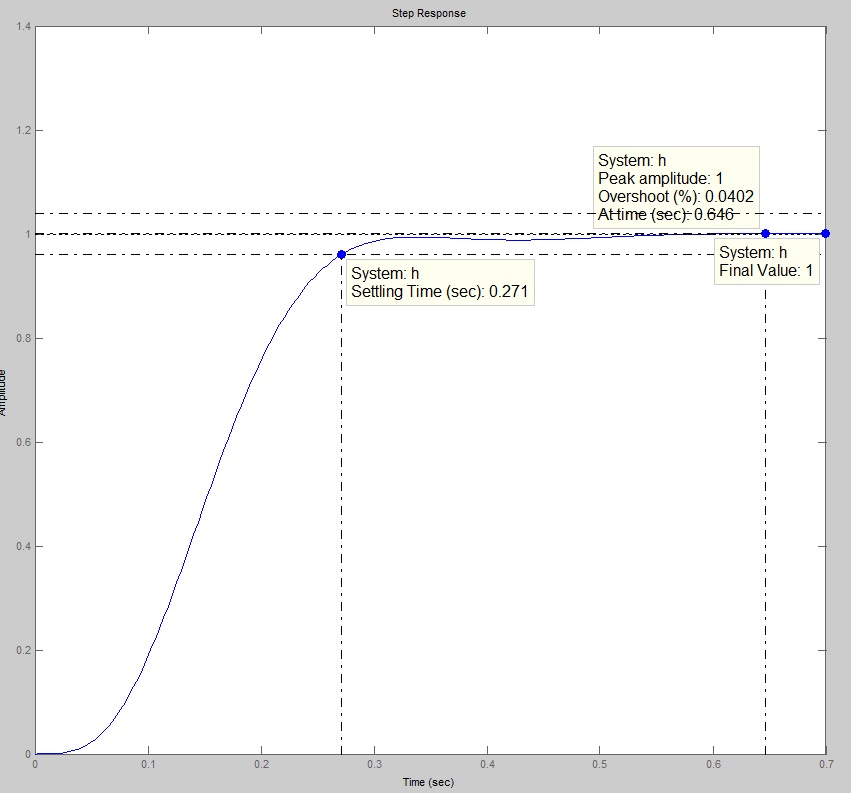
Рис.23
Задаем в рабочей области уравнение системы в матрично-векторном виде:
>> a=[0 0.01 0 0; 0 0 1 0; 0 -1/(0.03584*0.0372) -1/0.0372 0.528/(0.03584*0.0372);-0.613*220*0.9*10/0.03 -0.0041*0.9*10/0.03 0 -1/0.03]
>> b=[0;0;0;0.613*220*0.9*10/0.03]
>> c=[1 0 0 0]
>> d=0
>> h=ss(a,b,c,d)
>> step(h)
Выводится переходная характеристика аналогичная Рис.23.
Определим корни исходной системы:
>> h2=tf(h)
>> pole(h2)
ans =
-10.8380 +18.7596i
-10.8380 -18.7596i
-24.7437
-13.7954
Для уменьшения времени регулирования увеличим корни в 3 раза:
>> p=[-24.7437*3 -13.7954*3 -10.8380*3+18.7596i*3 -10.8380*3-18.7596i*3]
>> K=acker(a,b,p)
K =
80.0001 0.0357 0.0006 0.0030
Используя zpk форму проверим переходной процесс полученной модели:
>> h3=zpk([],[-74.2311 -41.3862 -32.5140+56.2788i -32.5140-56.2788i],1000)
>> step(h3)
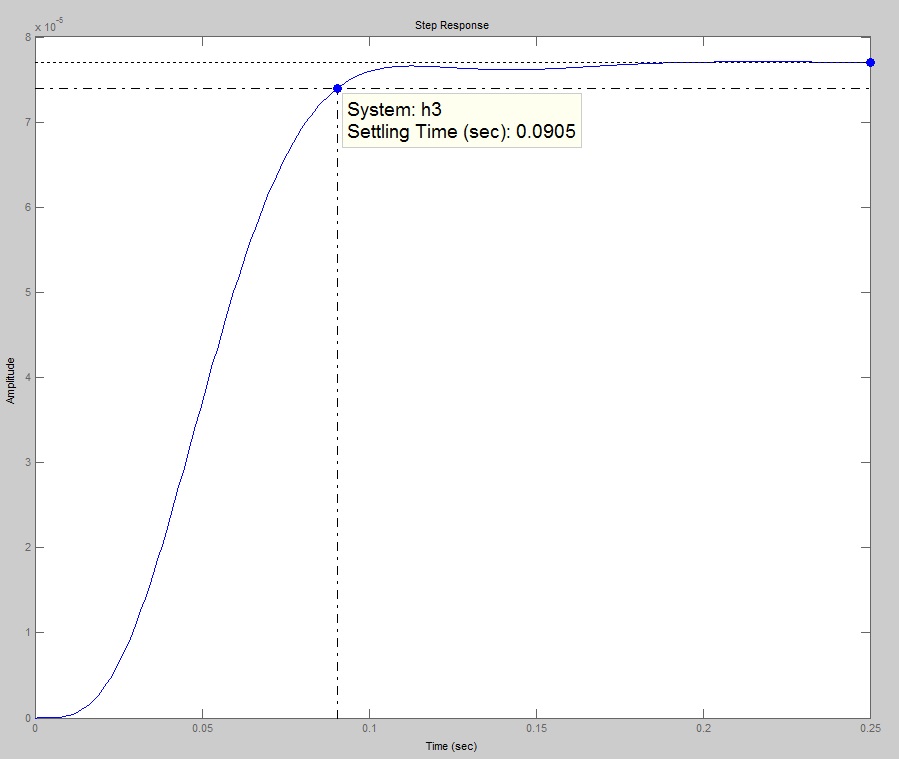
Рси.24
Переходной процесс имеет время в 3 раза меньше чем в исходной системе.
7.2.Структурная схема и векторно-матричное описание системы с модальным регулятором.
Формируем матрицу корней модального регулятора:
>> K=acker(a,b,p)
На Рис.25 представлена схема с модальным регулятором.
Рис.25
Определим коэффициент формы для определения hуст.
На Рис.26 представлена полученная ПХ.
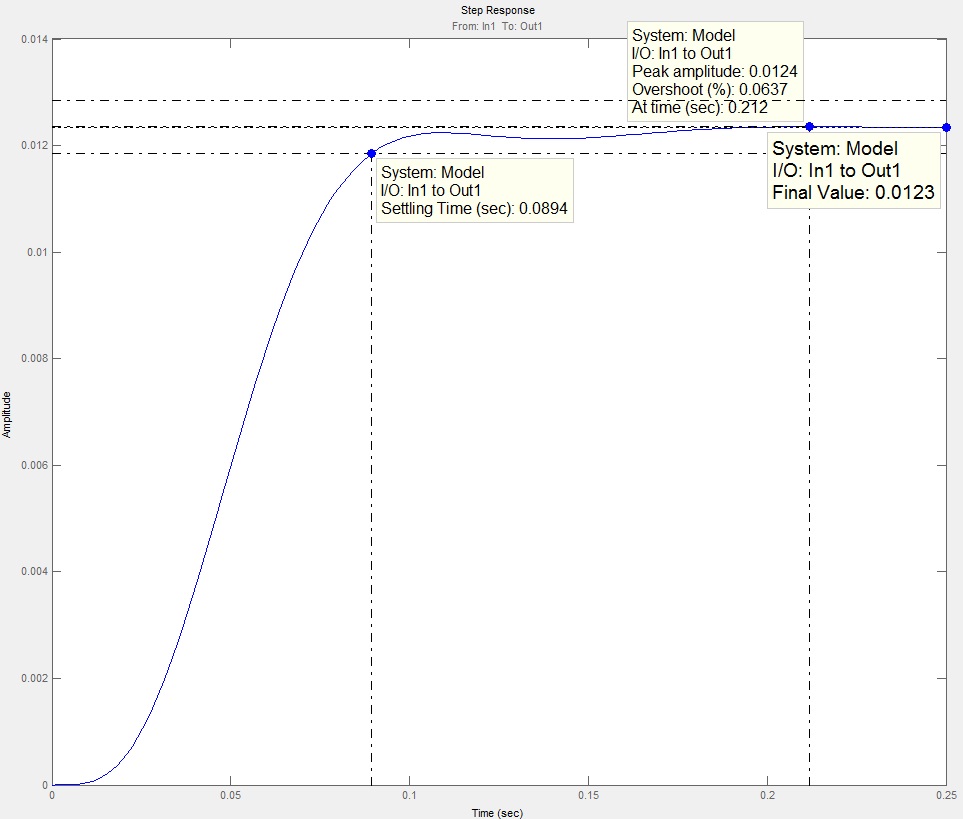
Рис.26
Вводим усилитель, так как установившееся значение не соответствует входному сигналу.
Коэффициент усилителя определяется как:
1/0.0123
На Рис.27 представлена схема с усилителем
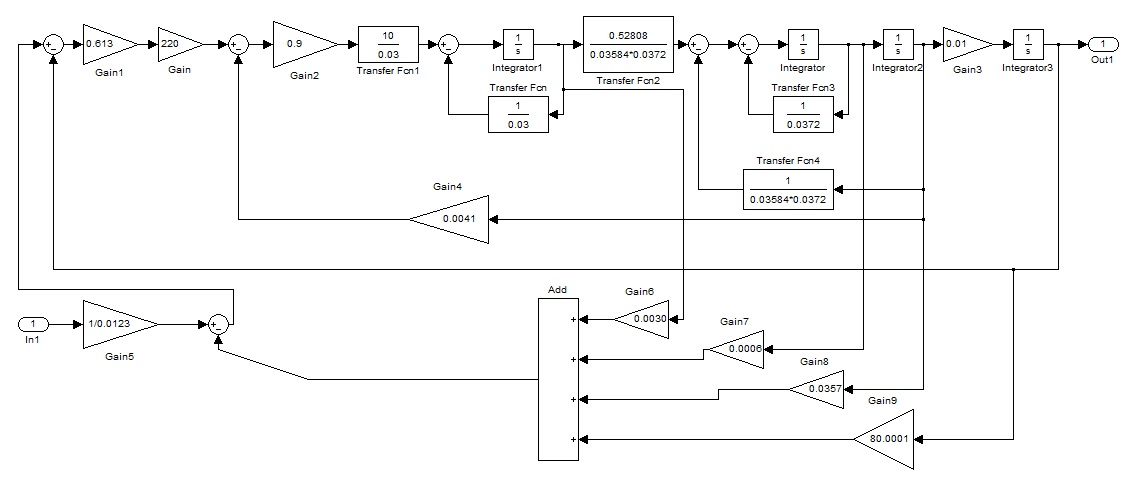
Рис.27
На Рис.28 представлена полученная ПХ.
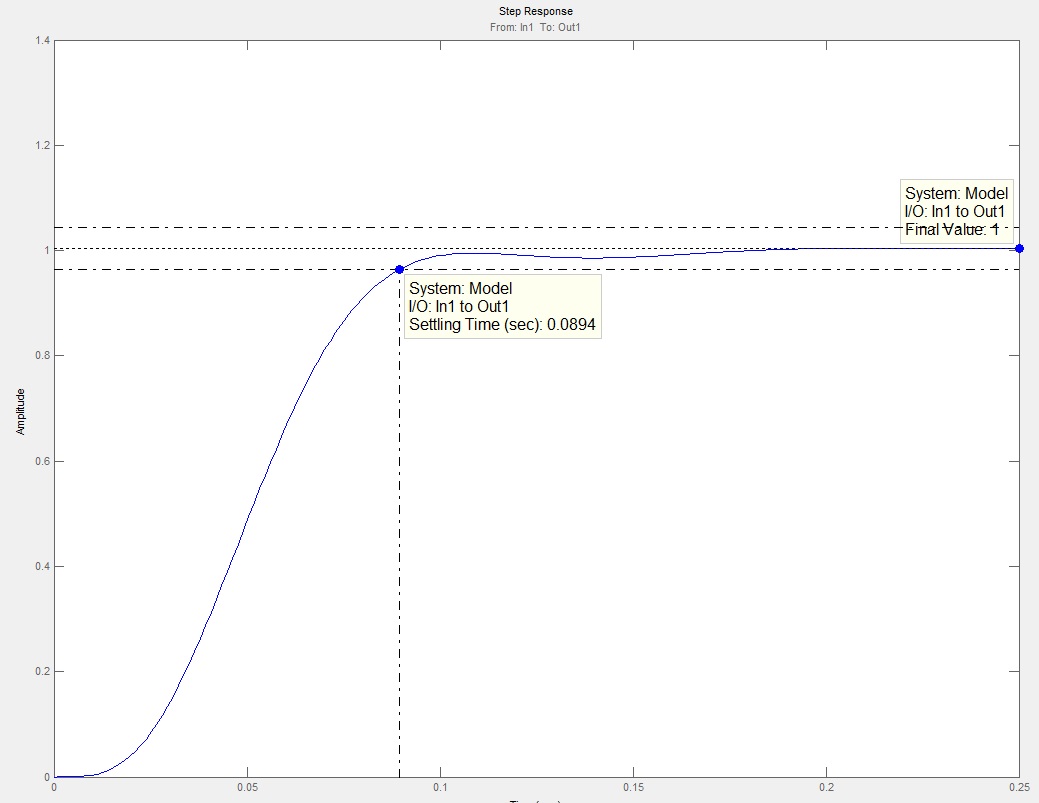
Рис.28
Получим переходной процесс всех переменных состояний:
>> h4=augstate(h3)
На Рис.29 представлены характеристики x1, x2, x3, x4.
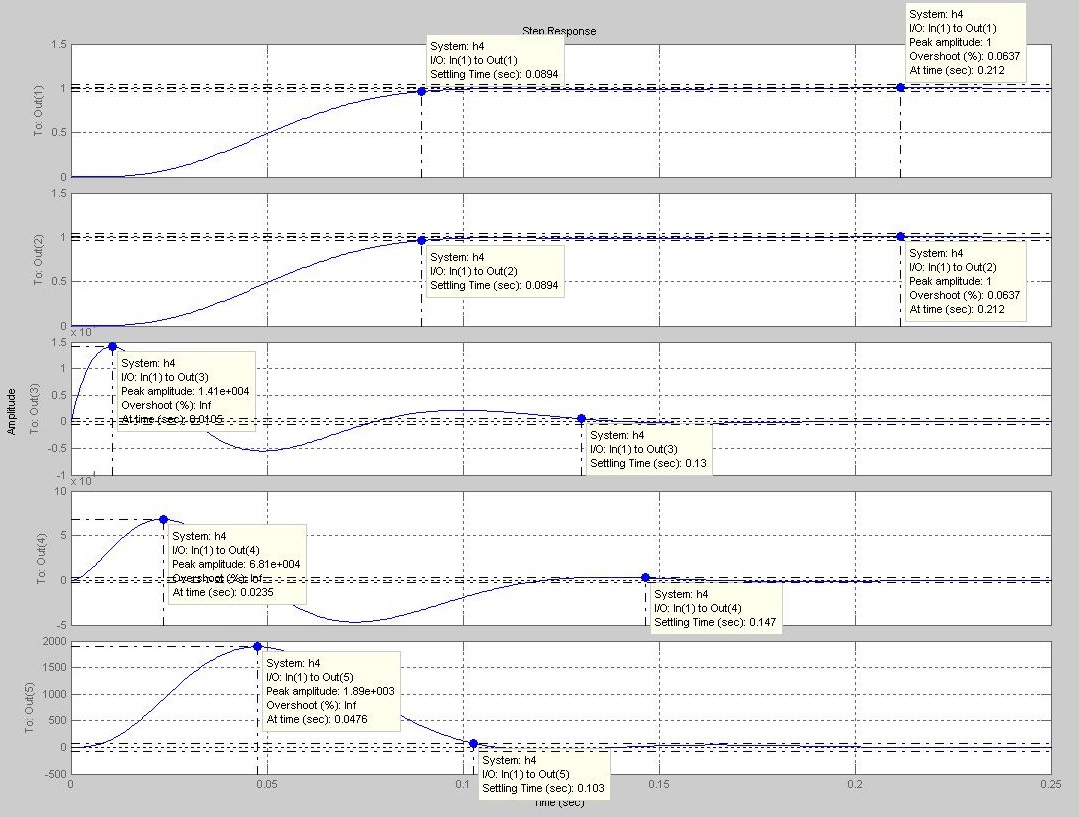
Рис.29