При всіх умовах попереднього параграфа многочлен будемо шукати у вигляді: .(1)

Поклавши в (1) , будемо мати: .(2) Взявши різницю і поклавши : , .(3) Взявши другу різницю і підставивши , отримаємо: , (4) і т. д.

Підставимо знайдені коефіцієнти в рівність (1):

- друга інтерполяційна формула Ньютона.

Позначимо: ,

,

.

Тому .

Зауваження: другу інтерполяційну формулу Ньютона зручно використовувати для інтерполяції та екстраполяції функції у випадку, коли близьке до .

Для оцінки похибки використовують формулу: .

Наприклад: маючи таблицю значень функції в межах від до з кроком знайти значення , .

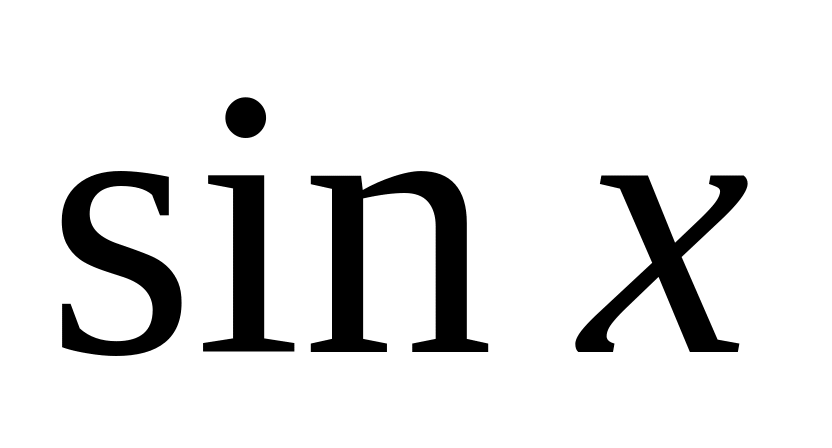
	0.2588	0.0832	-0.0026	-0.0006
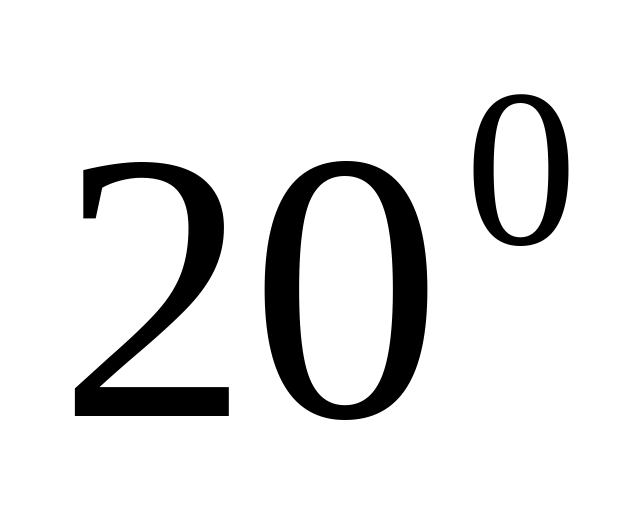
	0.3420	0.0800. 0.0806	-0.0032	-0.0006
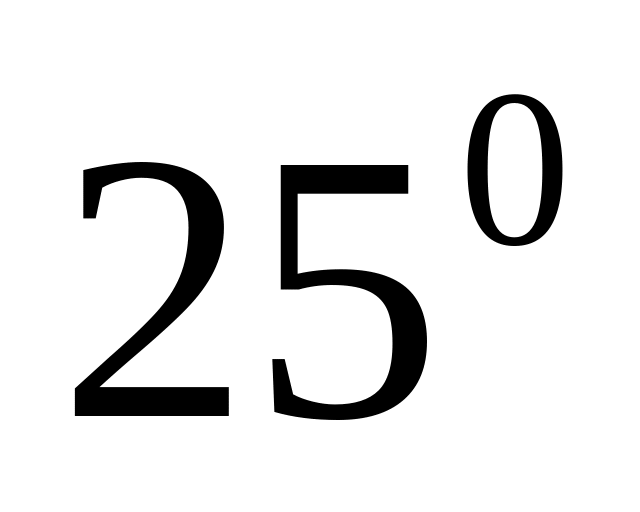
	0.4226	0.0774	-0.0038	-0.0006
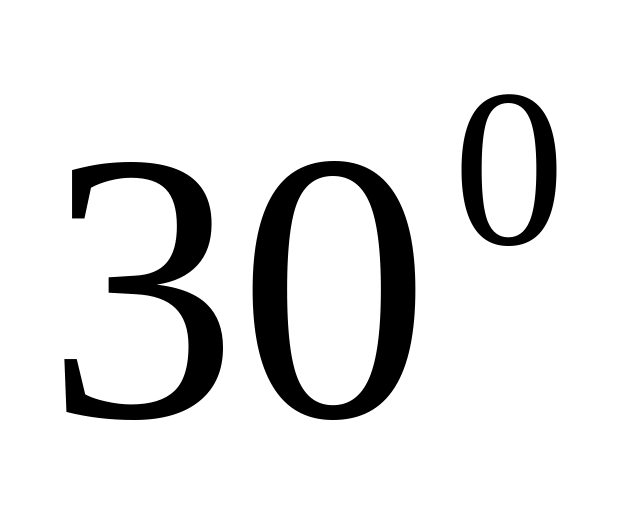
	0.5	0.0736	-0.0044	-0.0006
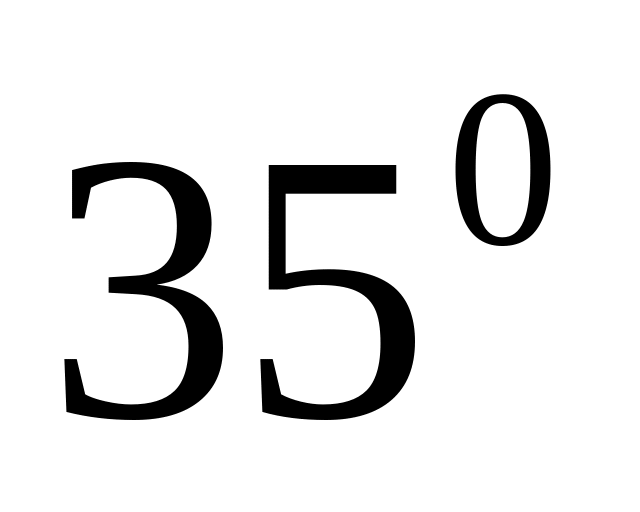
	0.5736	0.0692	-0.0049	-0.0006
	0.6428	0.0643	-0.0054	-0.0005
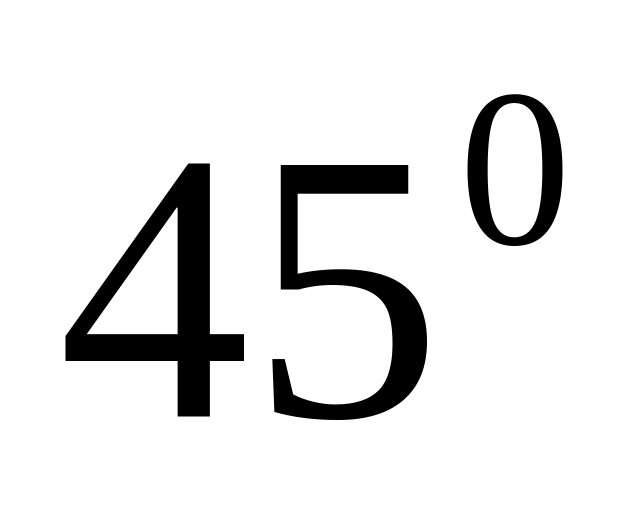
	0.7071	0.0589	-0.0057
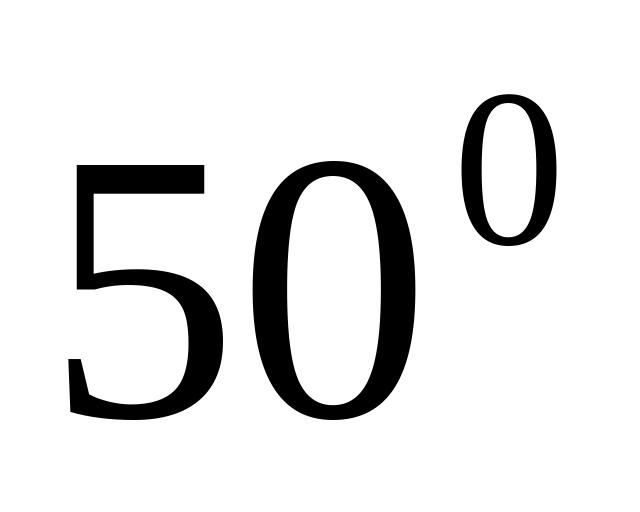
	0.7660	0.0532
	0.8192

.

.

§8

ПОСТАНОВКА ЗАДАЧІ ЧИСЕЛЬНОГО ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЇ.

Якщо функція f(x) задана таблично або складним аналітичним виразом, то для знаходження її похідних використовують чисельне диференціювання. Для цього на , який поділений на частини точками будують інтерполяційну функцію , а далі вважають, що , …, при цьому похибка , .

Якщо в околі деякої точки виконується , то це не означає, що .

Операція наближеного диференціювання менш точна ніж інтерпуляція.

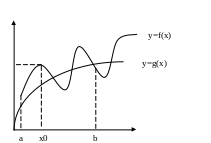
Менше наближення чим більш співпадають дотичні. Невелика різниця між значеннями f(x) і g(x) в точці , зовсім не гарантує такоїж невеликої різниці між значеннями похідних цих функцій.

§9

Диференціювання функцій інтерпольованих многочленами ньютона.

Нехай нескінченно-диференційовна на функція задана своїми значеннями в точках , . Замінимо цю функцію на першим інтерполяційним поліномом Ньютона:

Врахувавши, що похідна:

Зауваження: за слід вибирати вузол інтерполяції, який знаходиться найближче до точки , в якій шукаємо похідну.

Якщо потрібно знайти похідну в вузлі інтерполяції, тоді , .

§10

ДИФЕРЕНЦІЮВАННЯ ФУНКЦІЙ ІНТЕРПОЛЬОВАНИХ МНОГОЧЛЕНАМИ ЛАГРАНЖА.

Залишимо в силі умови попереднього параграфа. Замінимо функцію інтерполяційним многочленом:

, поділимо кожну дужку на і домножимо на .

тоді ,

,

підставимо .

Тоді . Похибка у випадку многочлена Лагранжа рівна: ,

.

У випадку, коли , тоді .

Зауваження: часто похибка, яка виникає при обчисленні похідних може набагато перевищувати похибку задання самої функції(навіть може зростати до ).

Наприклад:

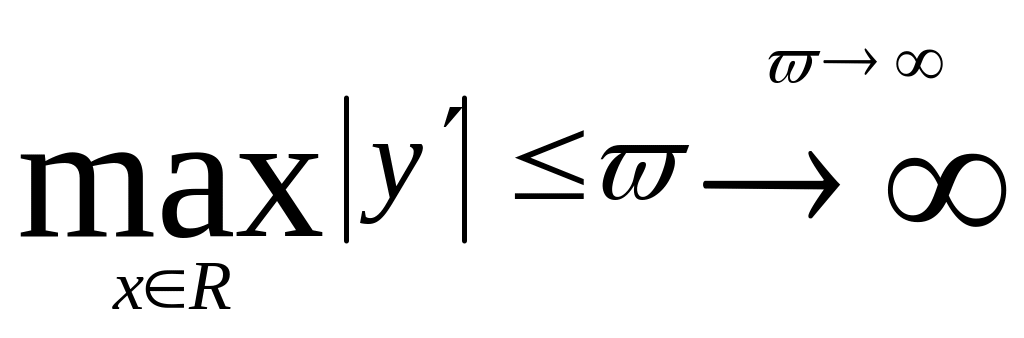
§11