Доведення
З формули (1)
.
Вважаючи оператор
як умовний множник
,
застосувавши останнє співвідношення
разів і застосувавши біном Ньютона
отримаємо:
необхідна формула.
Якщо
функція
задана табличними значеннями
,
точки
-
рівновіддалені,
,
то скінченні різниці зручно записувати
у вигляді таблиць.
Розглянемо
це на прикладі: скласти горизонтальну
таблицю різниць функції
,
якщо
,
.
-
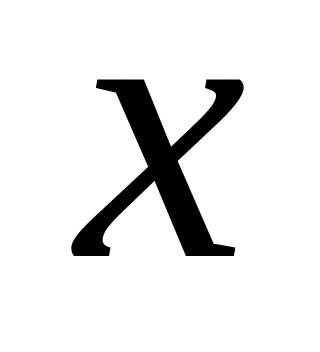
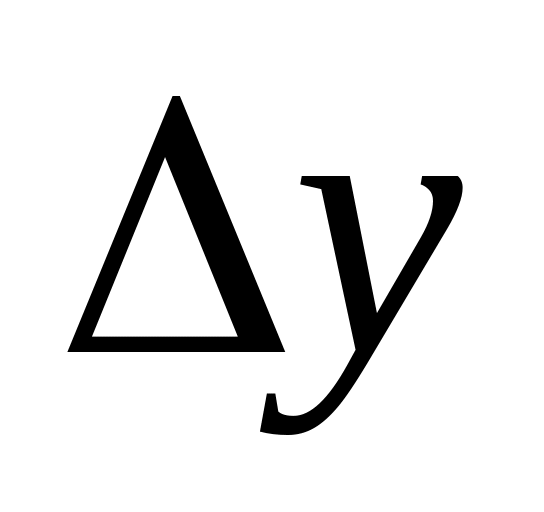
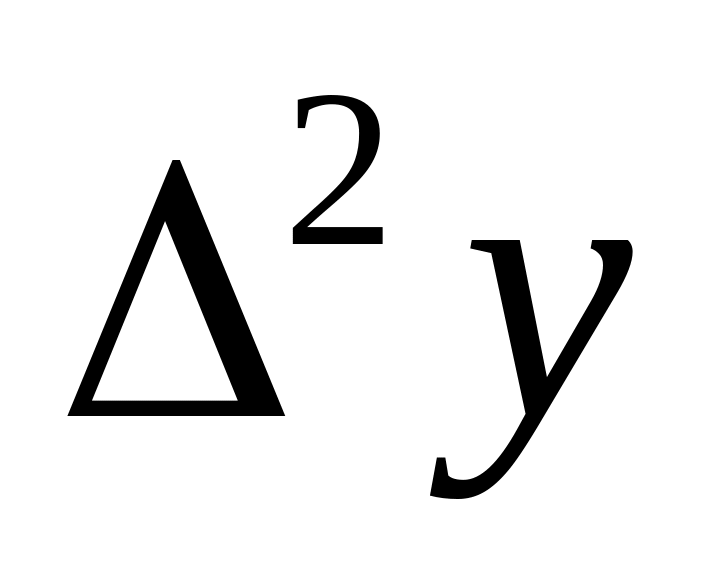
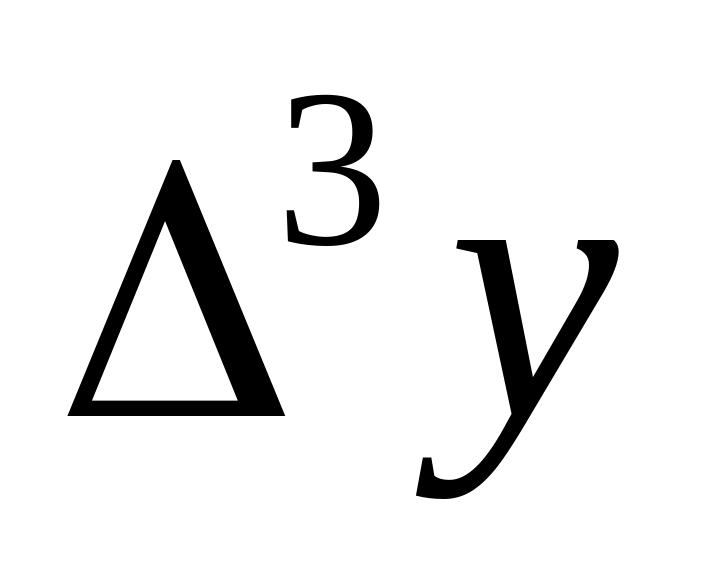
0
-1
3
8
12
1
2 2
11
20
12
2
13
31
32
12
3
44
63
44
4
107
107
5
214
7.
.
Скінчена різниця виражена через
послідовність значень функції.
§5
Узагальнена степінь
Означення:
-
тою узагальненою степінню числа
називається добуток
(1),
.
-нульова
узагальнена степінь
Властивість:
(2)
(доведення проводять методом математичної індукції)
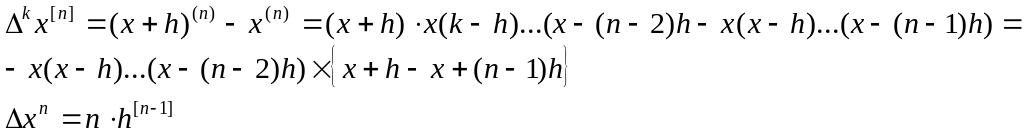
Припустимо, що для деякого натурального k виконується нерівність (2) тоді:
згідно
принципу математичної індукції рівність
(2) виконується для всіх натуральних k.
§6
ПЕРША ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА.
Нехай
задана таблиця значень функції
,
тобто дано, що
,
,
.
Поставимо завдання знайти поліном
:
і
для всіх
.
Остання умова еквівалентна тому, що
.
Многочлен
будемо шукати у вигляді: (1)
В дану рівність підставимо
:
.(2)
Обчислимо
першу скінчену різницю:
,
в дану рівність підставимо
:
(3)
.
,
підставивши
,
отримаємо:
,
.(4)
В
загальному випадку
.(5)
Формули (2), (3), (4), (5) підставимо в (1), отримаємо:
(6)- перший
інтерполяційний поліном Ньютона.
,
.
Для
використання на практиці формулу (6)
спрощують. Покладемо:
-
кількість кроків, яка необхідна для
того, щоб від точки
перейти до точки
.
Тоді
.
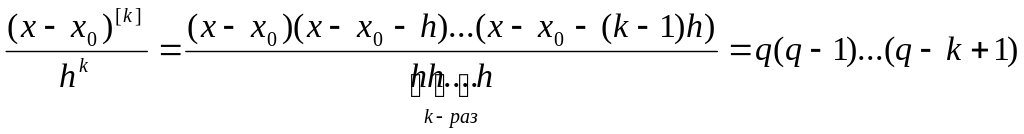З (6) будемо мати:
.
Зауваження:
якщо задана необмежена таблиця значень
функції, то число
вибирають так, щоб різниця
була сталою з заданою точністю. Першу
інтерполяційну формулу Ньютона зручно
використовувати для інтерполяції та
екстраполяції функції, коли
.
Для
оцінки похибки користуються формулою:
,
де
Наприклад:
знайти інтерполяційний поліном Ньютона
для функції
на відрізку
,
взявши
.
-
x
y
3.5
33.115
1.698
0.087
0.005
3.55
34.813
1.785
0.092
0.003
3.6
36.598
1.877
0.095
3.65
38.475
1.972
3.7
40.441
Бачимо,
що треті різниці дуже мало відрізняються,
беремо
.
§7
ДРУГА ІНТЕРПОЛЯЦІЙНА ФОРМУЛА НЬЮТОНА.