Розділ 3
§1
Постановка задачі інтерполяції
Нехай
на сегменті [a;b] задана система (n+1) точок:
.
Їх називають вузли інтерполяції. Задано
також значення в цих точках деякої
функції:
,
,…..,
.
Потрібно побудувати деяку функцію
(інтерполяційну
функцію), яка належить деякому класу
функцій і таку , що:
,
,…..,
.
Геометрично це означає: потрібно побудувати деяку криву певного типу, яка проходить через задану систему точок. Ці точки називаються вузлами інтерполяції.
Отриману інтерполяційну функцію використовуємо для знаходження значень функції в точках відмінних від вузлів інтерполяції. Така операція називається інтерполяція функцій.
Виділяють також поняття екстраполяції функції. Це той випадок, коли шукаємо значення функції в точці, яка не належить [a;b].
§2
ІНТЕРПОЛЯЦІЙНА ФОРМУЛА ЛАГРАНЖА.
На відрізку [a;b] задана система точок і задано значення функції в цих точках ( , , ,….., ). (1)
Потрібно
побудувати поліном
степеня
не вище
,
,
такий що:
,
.(2)
Спочатку
побудуємо поліном
,
такий що
(3). Оскільки на [a;b] згаданий поліном має
нулів, тому цей поліном можна записати
у вигляді:
.
Підставивши
,
отримаємо:
.
(4)
Знайденні
підставимо в (3)
Тоді :
.
(5)
Будуємо
многочлен
(6)
або
.(7)
Очевидно,
що степінь цього многочлена Лагранжа
.
, .
Формулу (7) можна записати в компактному вигляді:
,
.
Підставивши , отримаємо:
.
Врахувавши останні позначення, отримаємо:
.
При
многочлен Лагранжа - пряма, яка проходить
через точки
,
.
Приклад:
для функції
побудувати многочлен Лагранжа, взявши
вузли інтерполяції
,
,
.
§3
Коефіцієнти лагранжа. Оцінка похибки інтерполяції.
Вираз
(1)
називається коефіцієнтами Лагранжа.
Тоді многочлен Лагранжа набере вигляду:
(2).
Зауважимо, що форма коефіцієнтів Лагранжа
інваріантна відносно лінійної підстановки:
.
Це означає, що якщо
,
то отримаємо:
.
У випадку рівновіддалених вузлів інтерполяції вираз для коефіцієнтів Лагранжа спрощується.
Нехай
,
,
,…,
,
-
деякий крок.
,
,
.
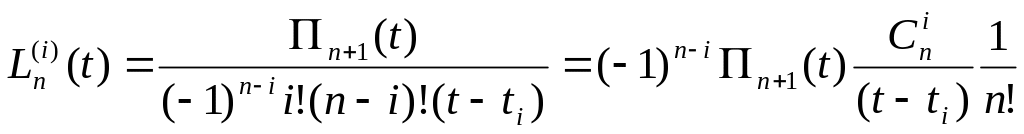Тоді
.(3)
Оцінимо
похибку
.
Нехай існують похідні функції
до
порядку включно, розглянемо функцію:
.
Очевидно, що
для всіх
.
Візьмемо деяку точку
:
,
.
Підберемо
так, щоб
,
тобто
.(4)
Тоді функція
на
має
корені і на кінцях відрізків
,
,…,
,
,…,
приймає однакові нульові значення. За
теоремою Рімана
має принаймні
нуль або більше,
має
нулів,...,
має хоча б один нуль.
Нехай
:
і
.
Оскільки
,
,
тому
.
Підставимо точку
:
,(5)
,
з (4) і (5) слідує:
.
Внаслідок
довільності вибору точки
і позначивши
,
отримаємо
(6)
Де
Приклад:
З якою
точністю можна обчислити
за допомогою формули Лагранжа для
функції
,
якщо за вузли вибрано
Скориставшись
формулою Лагранжа для задачі, то похибка
різниці на
§4
Cкінченні різниці
Нехай
задана функція
.
Позначимо
-
скінченну величину приросту аргументу.
Означення:
вираз
(1) називається першою скінченною різницею
функції
.
Означення:
скінченною різницею порядку
функції
називають величину
,
Властивості:
Якщо
,
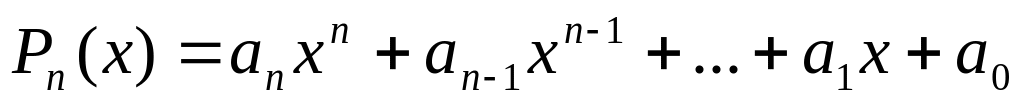то
.
( доведення
проводять методом підстановки, згідно
означення)
.
,
.
.
.
-
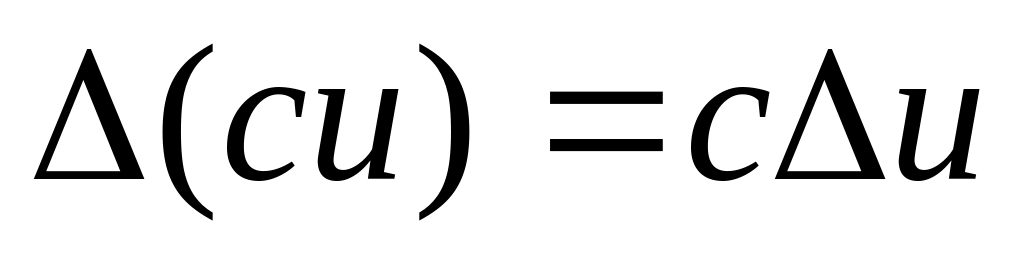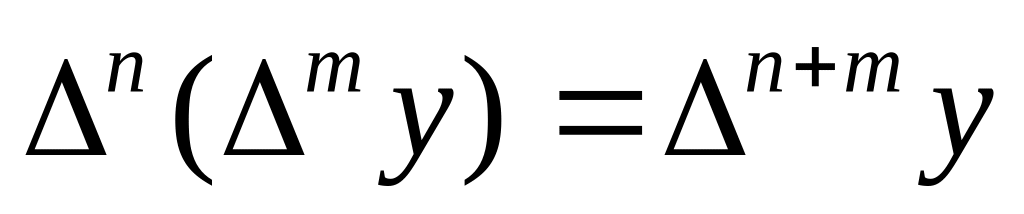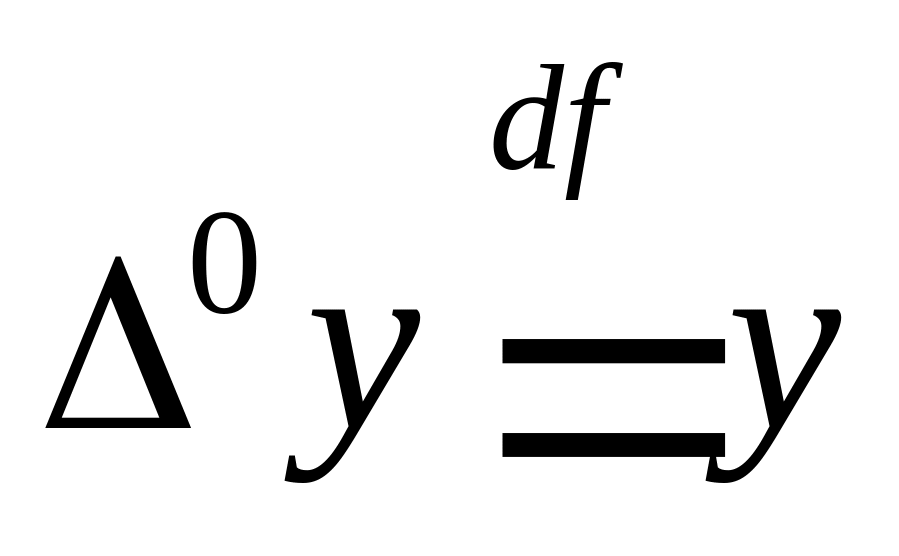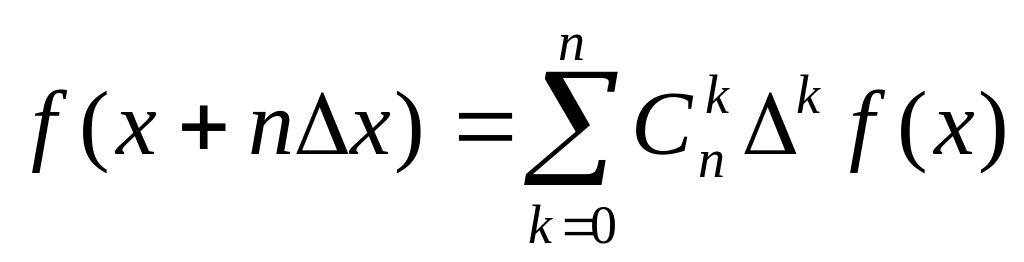формула, яка виражає послідовні значення
функції через її скінченні різниці.