
- •Розділ 1 наближення чисел
- •Чисельні методи розв’язування задач обчислювальної математики
- •Абсолютна і відносна похибки. Причини виникнення похибок
- •Похибки арифметичних дій
- •Доведення
- •Доведення
- •Загальна похибка для формули
- •Розділ 2 наближені розв’язки рівнянь та їх систем
- •Ітераційні методи розв’язування рівнянь. Принцип стискуючих відображень в метричному просторі.
- •Відокремлення коренів рівняння з однією змінною
- •Метод поділу відрізка пополам (метод дихотомії)
- •Доведення
- •Уточнення коренів рівняння методом хорд (метод пропорційних відрізків)
- •Доведення
- •Доведення
- •Метод простої ітерації для рівняння з однією змінною
- •Доведення
- •Метод Гауса
- •Ітераційний метод зейделя
- •Достатні умови збіжності ітераційних процесів
- •Доведення
- •Оцінка похибки наближень процесу ітерації.
- •Метод квадратних коренів
- •1 Етап: прямий хід.
- •Методи розв’язування нелінійних систем
- •Розділ 3
- •Постановка задачі інтерполяції
- •Коефіцієнти лагранжа. Оцінка похибки інтерполяції.
- •Cкінченні різниці
- •Доведення
- •Узагальнена степінь
- •При всіх умовах попереднього параграфа многочлен будемо шукати у вигляді: .(1)
- •Диференціювання функцій інтерпольованих многочленами ньютона.
- •Задача чисельного інтегрування функції. Формули прямокутників.
- •Використаємо розклад в ряд Тейлора функції f(X) в точці :
- •Квадратурні формули ньютона-котеса.
- •Формули трапеції.
- •Квадратурні формули сімпсона
- •Кусково-кубічна сплайн інтерполяція.
- •Деякі відомості про різницеві рівняння. Означення: Різницевим рівнянням називається рівняння відносно функції дискретної змінної.
- •Наближення функцій в лінійному нормованому просторі. Умови існування та єдності елемента найкращого наближення.
- •Середньоквадратичне наближення функцій.
- •N. 2 дискретне середньоквадратичне наближення.
- •N.3 середньоквадратичне наближення тригонометричними многочленами.
- •Найкраще рівномірне наближення. Теорема чебишева
- •Доведення
- •Теорема веєрштраса
- •Доведення
- •Доведення Леми
- •Доведення Теореми
- •§22. Тригонометричні многочлени найкращого наближення.
- •§23. Побудова алгебраїчних многочленів найкращого наближення.
- •Розділ 4
- •§1. Метод Ейлера.
- •§2. Модифікації методу Ейлера.
- •§3. Методи Рунге-Кутта.
- •§4. Метод Адамса
- •§5. Метод скінчених різниць для граничної задачі, для лінійного диференціального рівняння другого порядку з змінними коефіцієнтами.
- •§6. Метод прогонки розв’язування крайових задач для звичайних диференціальних рівнянь другого порядку.
Доведення
Нехай
-
розв’язок рівняння, щоб
використати принцип стискуючих
відображень потрібно показати окіл
точки
в якому похідна функції![]() задовольняє умову:
задовольняє умову:![]()
![]() .
Оскільки
неперервні
на [a,b],
то
.
Оскільки
неперервні
на [a,b],
то
![]() .
Тоді
.
Тоді
![]() .
Оскільки f(x)
неперервна, то в деякому околі
точки
буде
виконуватись:
.
Оскільки f(x)
неперервна, то в деякому околі
точки
буде
виконуватись:
![]()
![]() Далі можна застосовувати принцип
стискуючого відображення.#
Далі можна застосовувати принцип
стискуючого відображення.#
Для
оцінки точності користуються точністю
![]()
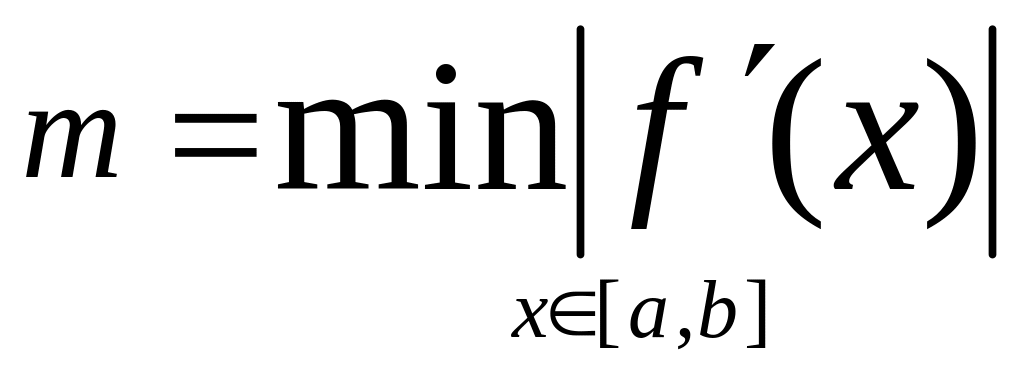
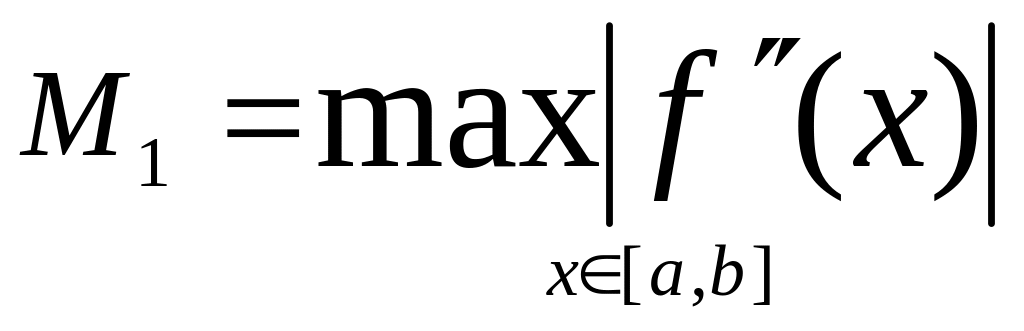
![]()
![]() (3)
(3)
Зауваження: метод дотичних не зручно використовувати тоді, коли в околі точки похідна набирає малих значень.
§6
Метод простої ітерації для рівняння з однією змінною
Нехай
(1), де
неперервна на
[a,b]
функція. Замінимо рівняння (1) рівносильним
рівнянням
![]() (2).
Виберемо грубо початкове наближення
і побудуємо послідовність:
(2).
Виберемо грубо початкове наближення
і побудуємо послідовність:
![]() (3).
(3).
Якщо
послідовність
![]() збігається до числа
збігається до числа
![]() ,
то перейшовши в (3) отримаємо:
,
то перейшовши в (3) отримаємо:![]() є розв’язком (2), а отже (1).
є розв’язком (2), а отже (1).
Виникають деякі запитання:
Які умови повинна задовольняти функція f(x), щоб послідовність (3) була збіжна
Як з(1) отримати (2), щоб функція забезпечувала збіжність послідовності (3)
Розглянемо графічно процес побудови ітерації:
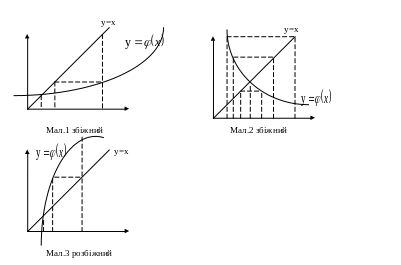
Теорема: нехай задовольняє наступним умовам:
визначена на [a,b]
неперервна на [a,b]
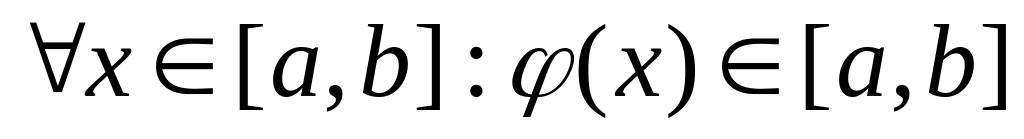
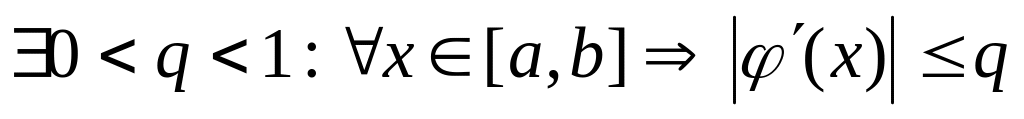 (4),
(4),
тоді
процес ітерації збіжний при довільному значенні
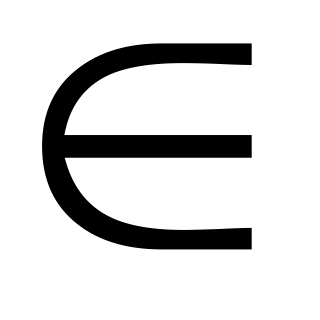 [a,b]
[a,b]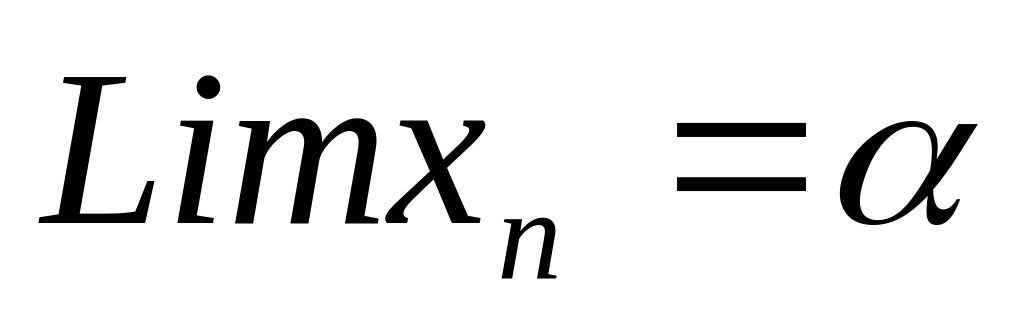 - єдиний
розв’язок рівняння (2)
- єдиний
розв’язок рівняння (2)справедлива оцінка:
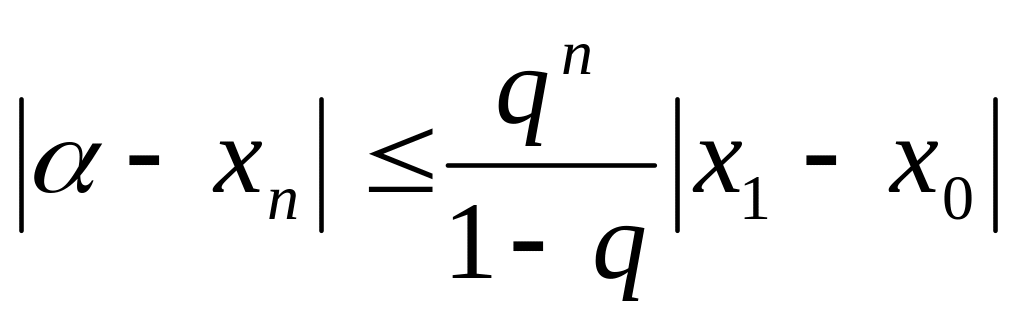 (5)
(5)
Доведення
Розглянемо
два послідовні наближення
![]() .
.
![]() .
Тоді
.
Тоді
![]() .
Будемо надавати числу n
значень: 1, 2, 3, ...
.
Будемо надавати числу n
значень: 1, 2, 3, ...
![]()
![]()
...
![]() (6)
(6)
Розглянемо
ряд
![]() ,
бачимо, що
,
бачимо, що
![]() .
З нерівності (6) слідує, що ряд збіжний,
тоді
.
З нерівності (6) слідує, що ряд збіжний,
тоді
![]() перейшовши до границі в (3) отримаємо,
що
- розв’язок рівняння (2).
перейшовши до границі в (3) отримаємо,
що
- розв’язок рівняння (2).
Доведемо
єдиність. Нехай
![]() тоді
тоді
![]()
![]()
![]()
остання
дужка завжди не дорівнює нулю.![]() .
Корінь єдиний. Візьмемо будь-яке число
.
Корінь єдиний. Візьмемо будь-яке число
![]() і
і
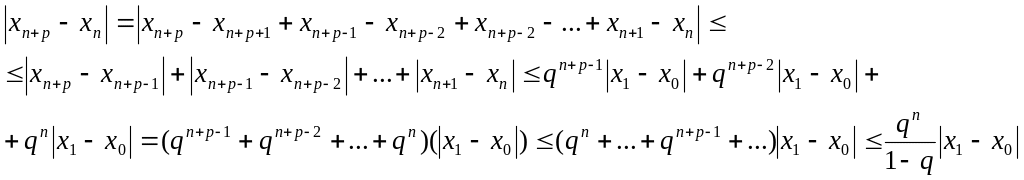 перейти
до границі при
перейти
до границі при
![]() отримаємо нерівність (5).
отримаємо нерівність (5).
Для
доведення (1) до виду (2) можна застосувати
такий метод. Замінимо рівняння (1)
рівносильним рівнянням
![]() де
де
![]() ,то
(1) (2) рівносильні. Та
,то
(1) (2) рівносильні. Та
![]() повинно бути таке, що
повинно бути таке, що
![]() ,
тобто
,
тобто
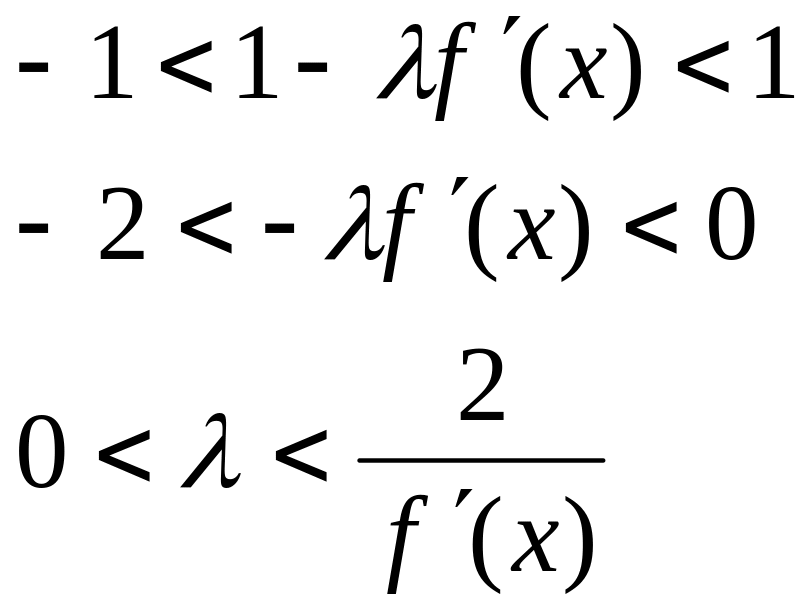 ,
тобто якщо знак функції
на [a,b]
не змінився, то
повинна мати той самий знак, що й
і
задовольняти нерівність
,
тобто якщо знак функції
на [a,b]
не змінився, то
повинна мати той самий знак, що й
і
задовольняти нерівність
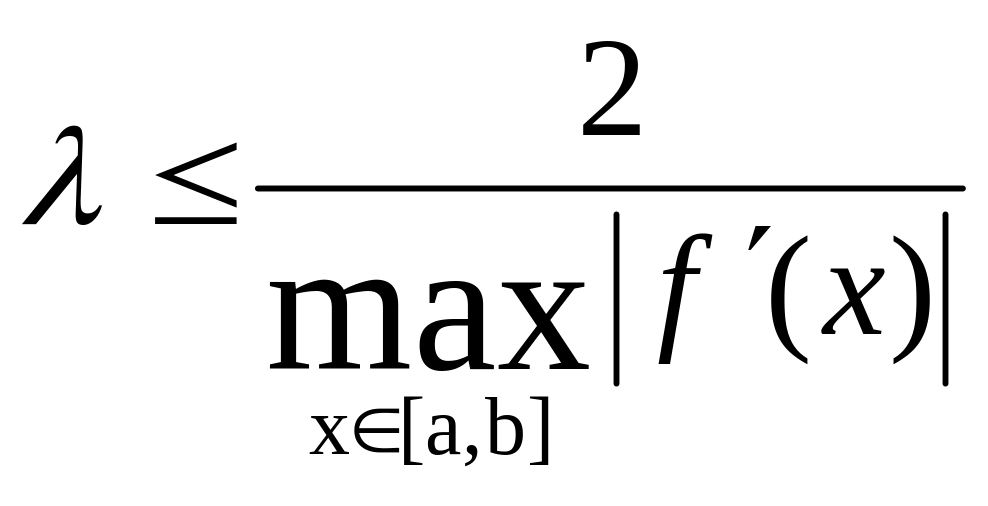 (7)
(7)
Н-д:
перетворити рівність
![]() ,
до виду
,
так щоб
задовольняла всі умови теореми, якщо
розв’язок
,
до виду
,
так щоб
задовольняла всі умови теореми, якщо
розв’язок
![]()
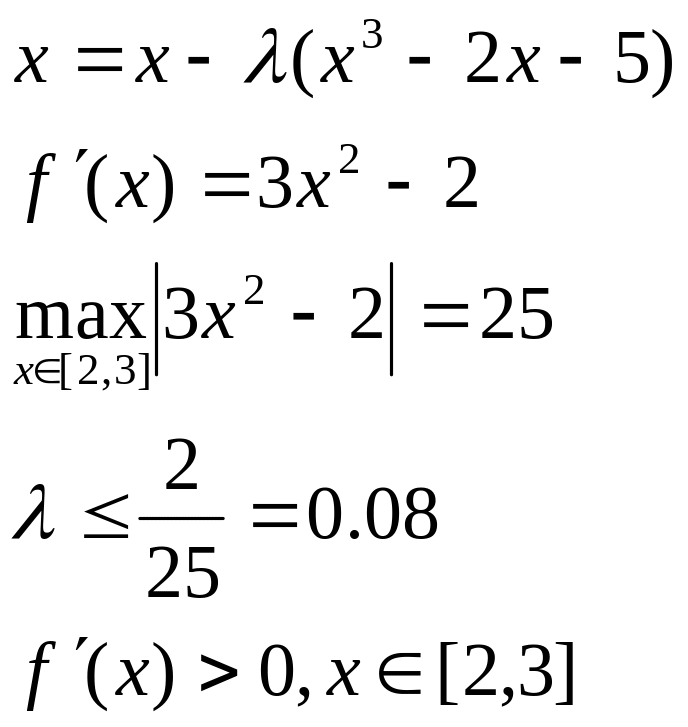
візьмемо =0.079, тоді отримаємо
![]()
вхідні
дані
![]() оцінка точності.
оцінка точності.
Зауваження:
для оцінки точності на практиці зручно
користуватися формулою:
![]() (8)
(8)
Метод Гауса
Теоретичні відомості
Найпростішим методом розв’язування систем лінійних алгебраїчних рівнянь є метод послідовного включення змінних, або метод Гауса. Є кілька модифікацій цього методу. Розглянемо схему єдиного ділення, за якою систему розв’язують в два етапи. На першому етапі вихідну систему рівнянь зводять до рівносильної їй системи трикутної форми. Цей процес перетворення називають зворотним ходом, знаходять розв’язок лінійної системи рівнянь трикутної форми.
Обмежимося розглядом системи трьох рівнянь з трьома змінними
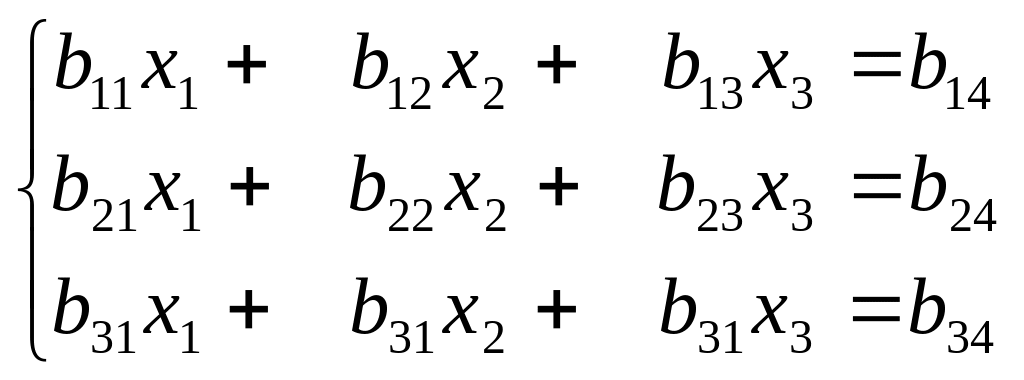 (1)
(1)
визначник
![]() якої не дорівнює нулю.
якої не дорівнює нулю.
Нехай
![]() ≠0.
Поділимо коефіцієнти першого рівняння
системи (1), включаючи й вільний член, на
коефіцієнти
.
Дістанемо нове рівняння
≠0.
Поділимо коефіцієнти першого рівняння
системи (1), включаючи й вільний член, на
коефіцієнти
.
Дістанемо нове рівняння
![]() (2)
(2)
де
![]() ,
(j=2,3,4).
(3)
,
(j=2,3,4).
(3)
Включимо
тепер змінну
![]() з другого боку і третього рівнянь системи
(1). Для цього рівняння (3) помножимо
послідовно спочатку на коефіцієнт
з другого боку і третього рівнянь системи
(1). Для цього рівняння (3) помножимо
послідовно спочатку на коефіцієнт
![]() і віднімемо його від другого рівняння
системи (1), а потім на
і віднімемо його від другого рівняння
системи (1), а потім на
![]() і віднімемо від третього рівняння
системи (1). Дістанемо систему двох
рівнянь з двома змінними
і віднімемо від третього рівняння
системи (1). Дістанемо систему двох
рівнянь з двома змінними
![]()
![]() .
.
![]() (
4)
(
4)
де
коефіцієнти
![]() обчислюються за формулами
обчислюються за формулами
![]() (і=2,3;
j=2,3,4).
(5)
(і=2,3;
j=2,3,4).
(5)
Далі
поділимо коефіцієнти першого рівняння
системи (4) на
![]() .
Дістанемо рівняння
.
Дістанемо рівняння
![]() (
6)
(
6)
![]() ,
(j=3,4).
(7)
,
(j=3,4).
(7)
Із
системи (4) виключимо змінну
![]() .
Дістанемо рівняння
.
Дістанемо рівняння
![]() ,
(8)
,
(8)
де
![]() ,
(j=3,4)
( 9)
,
(j=3,4)
( 9)
З рівняння (8) маємо
![]() ,
(10)
,
(10)
Після трьох кроків перетворення дістанемо систему рівнянь трикутної форми
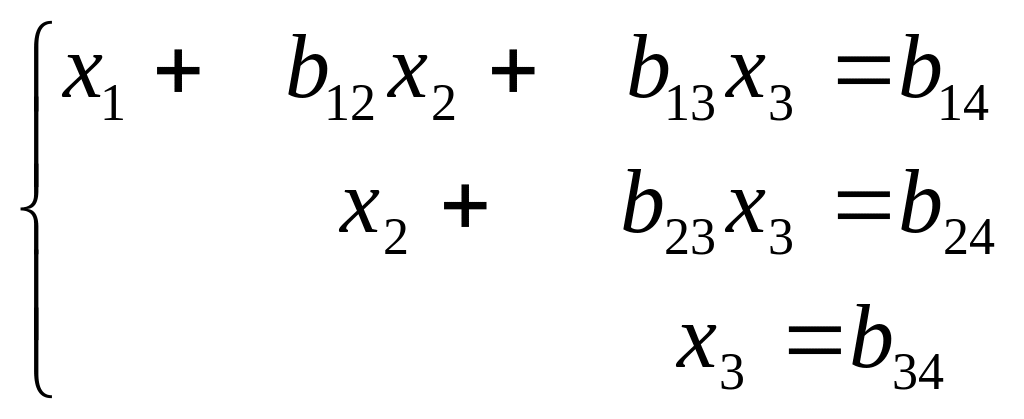 (11)
(11)
яка еквівалентна системі (1).
На цьому
прямий хід методу Гауса завершено.
Описаний процес перетворень системи
(1) до рівносильної їй системи (11) можна
здійснити, якщо виконуються умови
![]() 0,
0,
![]() 0,
0,
![]() 0.
0.
Оскільки системи (1) і (11) еквівалентні, то розв’язком системи (1) буде розв’язок системи (11), який можна записати так
![]()
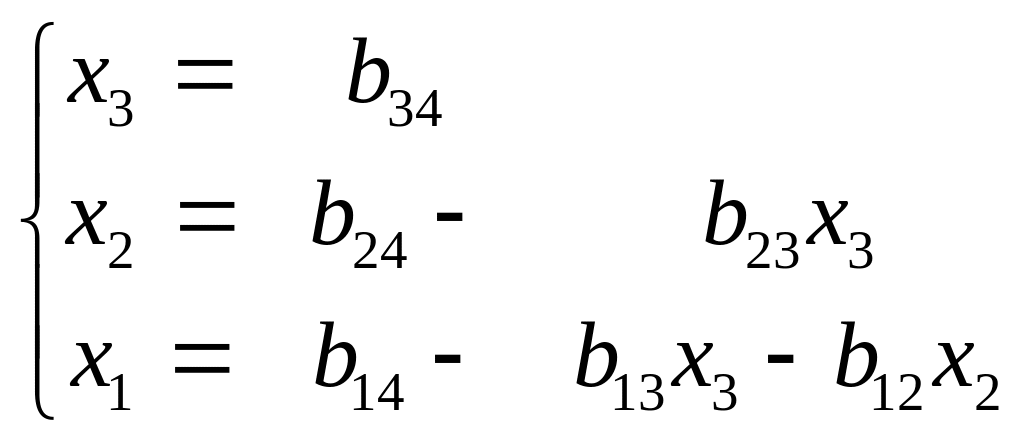 (12)
(12)
Цим завершено зворотній хід методу Гауса.
Приклад: Методом Гауса розв’язати систему рівнянь
![]() (13)
(13)
Коефіцієнти і вільні члени якої є точними числами.
Розв’язання:
переконаємось спочатку, що система не
вироджена і добре обумовлена. Для цього
підрахуємо визначник системи:
=9,035498.
Значення визначника системи становить
361% значення найбільшого коефіцієнта
системи
![]()
За схемою єдиного ділення систему розв’язуємо в такий спосіб.
Коефіцієнти і вільні члени системи (13) записуємо у перші три рядки (стовпці 3-6) табл..1 Підраховуємо контрольні і рядкові суми, які збігаються між собою, і записуємо їх у 7-му і 8-му стовпцях.
Таблиця 1
Крок перетворення |
Рядок |
Коефіцієнт
при змінних
|
Вільний член |
Контроль |
||||
Контрольна сума |
Рядкова сума |
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1 |
1 2 3 |
2,5 0,87 0,26 |
0,94 2,3 0,97 |
0,36 0,76 2,15 |
6,804 8,415 8,877 |
10,604 12,345 12,257 |
10,604 12,345 12,257 |
|
2 |
4 5 6 |
1 |
0,376 1,9729 0,8722 |
0,144 0,6347 2,1126 |
2,7216 6,0472 8,1694 |
4,2416 8,6548 11,1542 |
4,2416 8,6548 11,1542 |
|
3 |
7 8 |
|
1 |
0,3217 1,8320 |
3,0651 5,4960 |
4,3868 7,3280 |
4,3868 7,3280 |
|
4 |
9 10 11 |
|
1 |
1 |
3,0000 2,1000 1,5000 |
4,0000 3,1000 2,5000 |
4,0000 3,1000 2,5000 |
|
Усі числа першого рядка, крім рядкової суми, ділимо на . Результати ділення записуємо в четвертий рядок. Усі проміжні обчислення виконуємо з двома запасними десятковими розрядами. Рядкова сума 1+0,376+0,144+2,7216=4,2416 збігається з контрольною сумою 10,604:2,50=4,2416, а це означає, що випадкових помилок немає.
Обчислюємо коефіцієнти
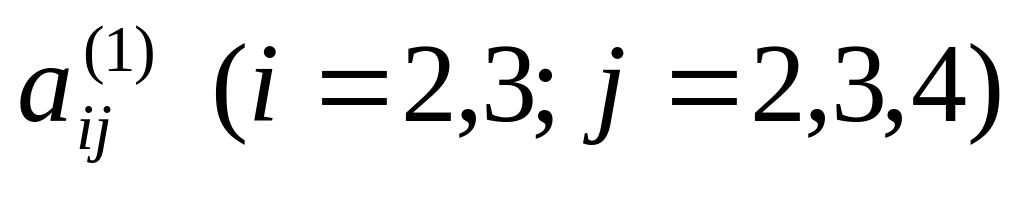 системи (4) за формулою (5) і записуємо
системи (4) за формулою (5) і записуємо
Їх у 5-ий і 6-ий рядки. Контрольні суми
12,345-0,87*4,2416=12,345-3,690=8,6548,
12,257-0,26*4,2416=12,257-1,103=11,1542
Збігаються з відповідними рядковими сумами
1,9729+0,6347+6,0472=8,6548,
0,8722+2,1126+8,1694=11,1542
А це означає, що обчислення виконано правильно.
4.
Усі числа рядка 5, крім числа, що стоїть
і 8-му стовпці, ділимо на
![]() ,
і результати записуємо в 7-й рядок.
Контрольна сума дорівнює 8,6548:1,9729=4,3868 ,
івона збігається з рядковою сумою
,
і результати записуємо в 7-й рядок.
Контрольна сума дорівнює 8,6548:1,9729=4,3868 ,
івона збігається з рядковою сумою
1+0,3217+3,0651=4,3868.
5.
Коефіцієнт
![]() рівняння
(8) обчислюємо за формулами (9) і записуємо
в 8-й рядок. Контрольна сума
11,1542-4,3868*0,8722=7,3280 збігається з рядковою
1,8320+5,4960=7,3280.
рівняння
(8) обчислюємо за формулами (9) і записуємо
в 8-й рядок. Контрольна сума
11,1542-4,3868*0,8722=7,3280 збігається з рядковою
1,8320+5,4960=7,3280.
6.Зворотний хід виконуємо за формулами (12). При цьому використовуються 8-й, 7-й і 4-й рядки таблиці 1. з 8-го рядка дістаємо:
![]() =5,4960:1,8320=3,0000;
=5,4960:1,8320=3,0000;
![]() =7,3280:1,8320-4,0000.
=7,3280:1,8320-4,0000.
З 7-го рядка маємо:
=3,0651-0,3217*3=2,1000
![]() =4,3868-0,3217*4=3,1000.
=4,3868-0,3217*4=3,1000.
Нарешті, з 4-го рядка знаходимо:
=2,7216-0,144*3-0,376*2,1=1,5000,
![]() =4,2416-0,144*4-0,376*3,1=2,5000.
=4,2416-0,144*4-0,376*3,1=2,5000.
Обчисленні
значення
![]() і
і
![]() зв’язані
між собою співвідношенням
=
+1
(j=1,2,3),що
свідчить про відсутність випадкових
обчислювальних помилок.
зв’язані
між собою співвідношенням
=
+1
(j=1,2,3),що
свідчить про відсутність випадкових
обчислювальних помилок.
§8
МЕТОД ПРОСТОЇ ІТЕРАЦІЇ РОЗВ’ЯЗУВАННЯ СИСТЕМИ ЛІНІЙНИХ, АЛГЕБРАЇЧНИХ РІВНЯНЬ
Нехай
задано система рівнянь:![]() (1)
(1)
Або
![]() (2).
(2).
Розв’яжемо
кожне і-те рівняння відносно змінної
![]()
![]() .
.
![]() (3), або
(3), або
![]() (4).
(4).
Виберемо
початкове наближення
![]() і побудуємо послідовність за формулою
і побудуємо послідовність за формулою
![]() (5).
(5).
Якщо отримана послідовність має границю, то ця границя є розв’язком (4), а отже й (2).
Зауваження: Для успішного застосування методу ітерації модулів ідеальних елементів системи (1) повинні бути великі в порівнянні з іншим модулем.
Зауваження:
в якості початкового наближення вибирають
вектор
![]() ,
хоча не обов’язково –
можна брати довільний вектор. Тому
процес ітерації має властивість
самовиправлення, тобто окрема помилка
в обчисленнях не впливає на кінцевий
результат.
,
хоча не обов’язково –
можна брати довільний вектор. Тому
процес ітерації має властивість
самовиправлення, тобто окрема помилка
в обчисленнях не впливає на кінцевий
результат.
Твердження: Ітераційний метод буде збіжний, якщо матриці системи (1) всі діагональні елементи будуть більші за суму модулів усіх інших елементів відповідного рядка.
Теорема:
якщо для системи (1)
виконується одна з умов:![]() ,
,
![]() ,
то процес ітерації збігається до єдиного
розв’язку системи не залежно від вибору
початкового значення.
,
то процес ітерації збігається до єдиного
розв’язку системи не залежно від вибору
початкового значення.
Наслідок:
для системи (1) метод ітерації є збіжним
якщо
![]() .
.
Для зведення системи (1) до вигляду зручного до застосування процесу ітерації можна робити так:
Звідси слідує правило за яким систему (1) зводять до виду (3) для подальшої побудови ітерації.
З системи (1) вибираємо рівняння в яких є коефіцієнти, модулі яких більші за суму модулів всіх інших коефіцієнтів цього рівняння. Кожне з таких рівнянь ставимо на те місце в системі щоб виділений елемент був діагональним.
З невикористаних і виділених рівнянь системи складаємо лінійно незалежні комбінації так, щоб зберігався заданий принцип.
§9
