Метод поділу відрізка пополам (метод дихотомії)

 

Нахай задане рівняння . Нехай неперервна на і приймає на кінцях відрізка значення різних знаків.

 

 

 

Алгоритм:

1. Ділимо[a,b] пополам точкою х. визначимо чи f(x)=0.

2. Перевіряємо добуток f(x)f(a)>0.

3. Робимо до тих пір, доки

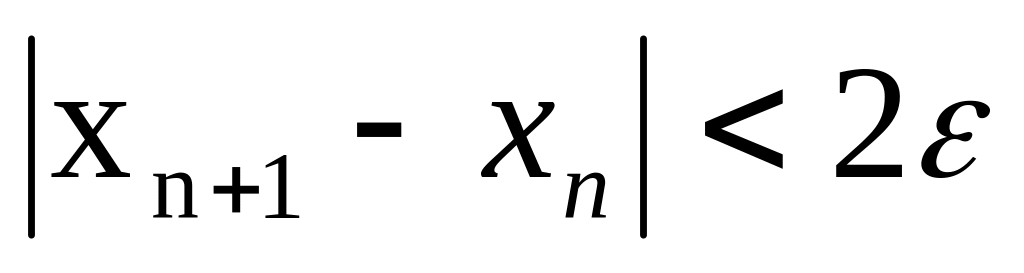
4. Знайдемо середину відрізка 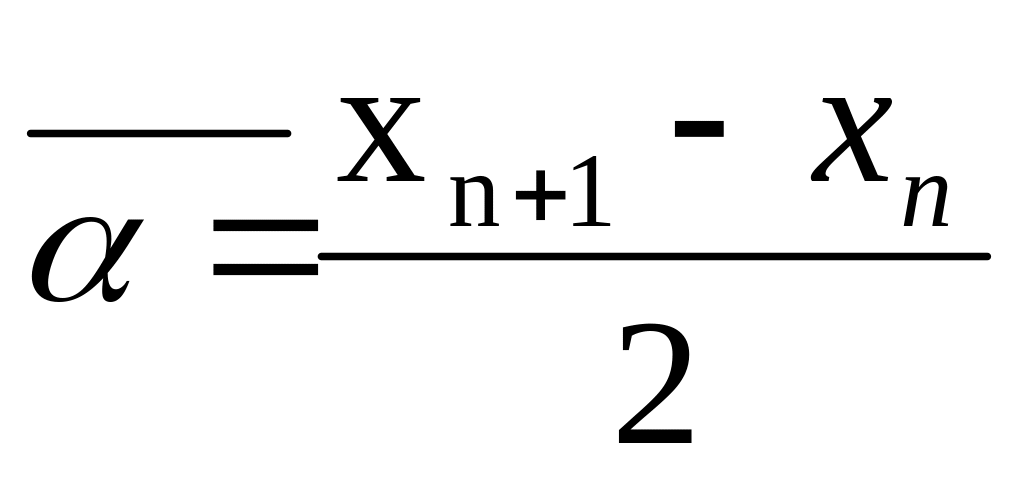(1)

Потрібний результат мажна отримати за вказаним алгоритмом.

Доведемо, що процес збіжний. . (2). Послідовність лівого кінця не спадає, а права не зростає, існує . Перейшовши до границі в (2)

Теорема: нехай точний розв’язок рівняння (1), наближений розв’язок і : , тоді справедлива рівність

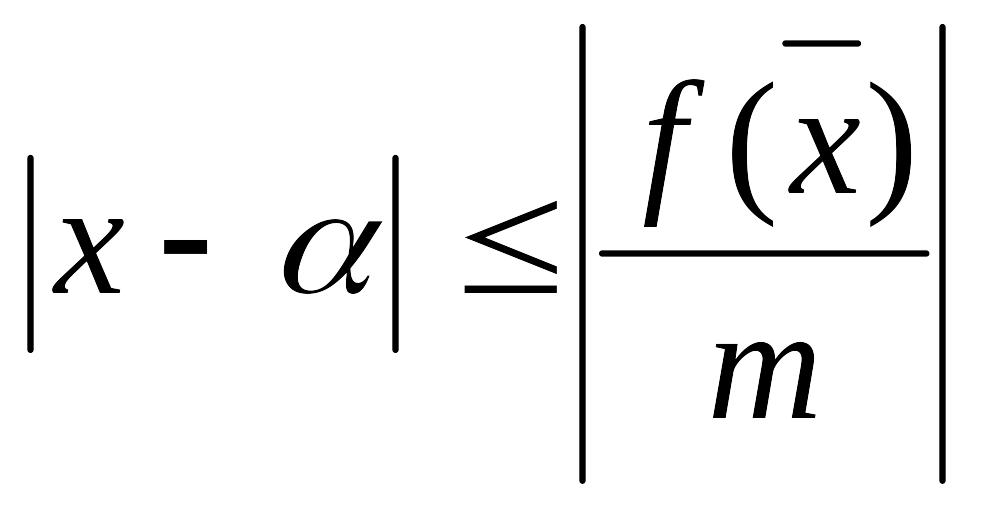
Доведення

За теоремою Лагранжа.

#

 

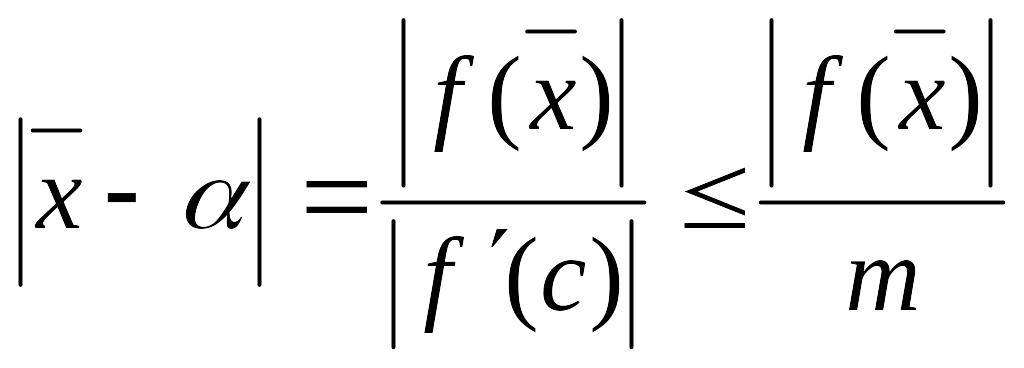§4

Уточнення коренів рівняння методом хорд (метод пропорційних відрізків)

 

Нехай дано рівняння . Залишимо в силі припущення попереднього параграфа. Розглянемо геометричну ітерацію методом хорд.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

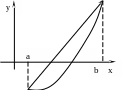
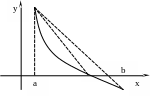
Мал.1 Мал.2

 

Виведемо рекурентну формулу для побудови наближення:

...

(2)

Доведемо збіжність даного процесу: послідовність монотонно зростає і обмежена зверху, тому , в рівнянні (2) перейдемо до границі:

Зауваження: в загальному випадку за нерухому точку вибирають той кінець відрізка [a,b] в якому знак функції f співпадає з знаком другої похідної, тоді (2 ) буде:

, (3)

Другий кінець проміжка зручно вибирати за початкове наближення.

Виведемо формулу для оцінки точності. Нехай похідна неперервна на [a,b], тоді вона приймає найбільше і найменше значення, тобто , , =0, де - розв’язок рівняння. Застосуємо теорему Лагранжа: . Розкривши душки додавши до обох частин рівності вираз і звівши подібні доданки, отримаємо: . Врахувавши межі зміни похідної (4) (5).

Виникає питання про можливість використання оцінки (5), коли мінімум похідної =0.

Відповідь про збіжність послідовності отриманої за рекурентною формулою (3) дає наступну теорему:

Теорема: нехай на відрізку [a,b] функція f(x) неперервна разом зі своїми похідними до 2-го порядку включно, причому . Нехай також похідні зберігають на [a,b] сталі знаки, тобі існує такий окіл кореня , що для початкового наближення з цього околу послідовність ( ), яка обчислюється за формулою (3), збігається до .

Доведення

Щоб скористатися принципом стискуючого відображення досить показати, що в деякому околі R кореня похідна функції , задовільняє умову .

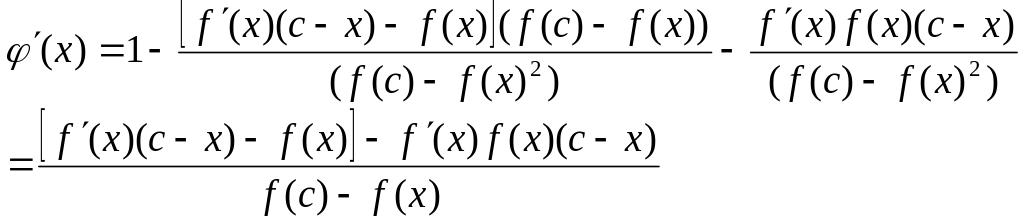
Підставимо : . Запишемо для f(x) формулу Тейлора і обмежимося 3-ма доданками, тобі: . Підставивши в останню рівність x=c, отримаємо: , оскільки при : то можна виділити такий окіл R:

§5

МЕТОД ДОТИЧНИХ (МЕТОД НЬЮТОНА)

Розглянемо геометричну інтерпритацію даного методу. Нехай маємо рівняння (1) і всі умови попереднього § виконуються. Беремо точку B, проводимо в ній дотичну.

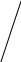
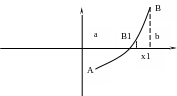
Рівняння дотичної в точці має вигляд , знайдемо точку :

(2)

Зауваження: в якості вихідної точки слід вибирати той кінець відрізка [a,b] в якому функція має той самий знак, що і її друга похідна.

У випадку зображеному на малюнку послідовність монотонно спадає і обмежена знизу, а отже вона збіжна, тобто . Перейшовши до границі в рівності (2) отримаємо: В загальному випадку справедлива така теорема.

Відповідь про збіжність дає наступна теорема:

Теорема: нехай на відрізок [a,b] функція f(x) неперервна разом з своїми похідними другого порядку включно, які зберігають знак і не перетворюються в нуль і крім того f(a)f(b)<0. Тоді існує деякий окіл розв’язку рівняння (1) що з цього околу послідовність обчислена за формулою (2) збігається до кореня .