Розділ 4

§1. Метод Ейлера.

Дано диференціальне рівняння , (1)

Вибираємо досить малий крок h, і будуємо систему рівновіддалених точок:

,

Інтервальну криву яка є розв‘язком рівняння (1) і проходить через точку , замінюємо ламаною . З вершинами ланки якої в вузлах (між вузлами) мають напрям який співпадає з напрямом інтегральної кривої (1), тому:

(2)

Геометрично, це означає:

1. Вибираємо полюс т .

2. Відкладаємо відрізок :

з врахуванням знаку, тоді кутовий коефіцієнт:

3. Через т проводять пряму паралельну до перетину з прямою

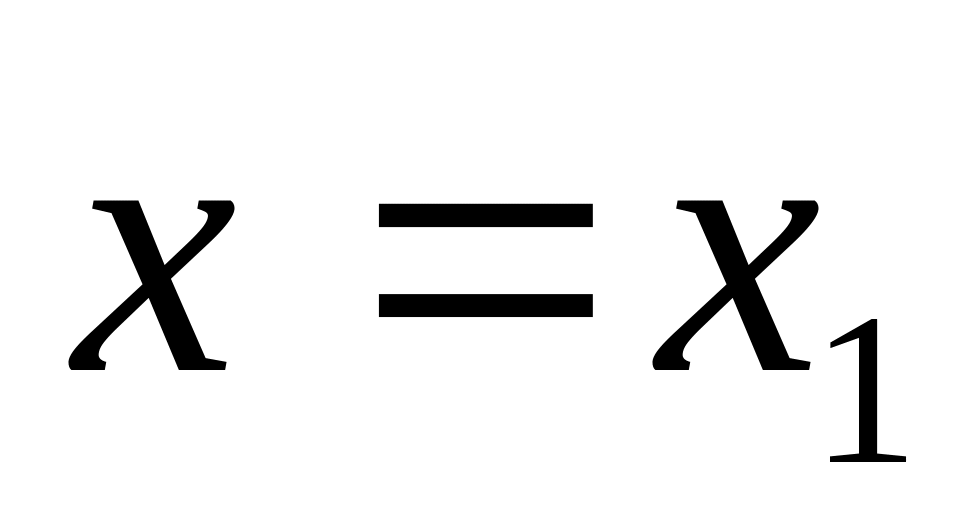
Відкладаємо

З формули (2) випливає (3) – Формула Ейлера.

§2. Модифікації методу Ейлера.

п.1. Удосконалений метод Ейлера.

Дано , (1)

Задано систему точок

1) Знаходимо т і

де :

2) Обчислюємо , тоді

3)

п. 2. Метод Ейлера-Коші.

1. Будуємо (це грубе наближення)

2. 

3. 

п. 3. Метод Ейлера-Коші з ітераційною обробкою ординат

1. Шукаємо початкові наближення:

2. Будуємо ітераційний процес:

3. В кінцевому випадку вважаємо що:

при деякому - крок на якому ми зупиняємось у пункті 2.

Процес ітерації продовжуємо до тих пір поки деякі і

наближення не співпадатимуть у відповідних десяткових знаках.

Зауваження: З усіх перерахованих методів останній дає похибку на кожному кроці, тому він використовується найчастіше.

Для порівняння метод Ейлера дає похибку .

§3. Методи Рунге-Кутта.

Задано диференціальне рівняння: (1) і початкова умова: .

Позначимо:

Вважатимемо, що має неперервні частинні похідні до деякого порядку , тоді розв‘язок має похідні порядку.

За формулою Тейлора:

Позначимо і відкинемо залишковий член:

(2)

Похідні які входять в праву частину (2) можуть бути обчислені:

Похідні обчислюються досить складно, тому практично використовувати їх незручно.

Рунге запропонував:

(4)

Таку лінійну комбінацію з сталими коефіцієнтами

де:

де:

(4)

і - сталі коефіцієнти.

Причому .

(5)

Сталі вибираються так щоб розклади (2) і (4) по степенях співпадали до якомога більших степенів , тобто так , щоб функція:

(6)

так щоб (6) задовольняла умови:

але при цьому похибка:

Надаючи різні значення будемо отримувати різні формули Рунне-Кутта.

Необхідно наступні величини:

1. Нехай , тоді з (6):

Тому:

В загальному випадку : , тобто (7)

2. , тоді

Таким чином отримаємо систему в якій кількість рівнянь менша ніж кількість невідомих:

(8)

Вибирати розв‘язки системи (8) треба так щоб отримувати якомога легші обчислення.

§4. Метод Адамса

Нехай задано диференціальне рівняння:

(1)

Задана система точок:

Очевидно:

(2)

В силу ІІ інтерполяційної формули Ньютона з точністю до різниць четвертого порядку, буде:

де: або

(3)

Вважаючи, що:

при цьому

Межі інтегрування змінюються на і підставивши (3) в (2) обчисливши інтеграл отримаємо:

- Формула Адамса

Для початку обчислень треба мати чотири початкових значення: . Їх шукають виходячи з початкової умови довільним іншим чисельним методом.