Теорема веєрштраса

Лема1: Справедлива рівність:

Доведення

Оскільки а=х, b=(1-х)

Лема2: Справедлива рівність:

Доведення Леми

Маємо суму

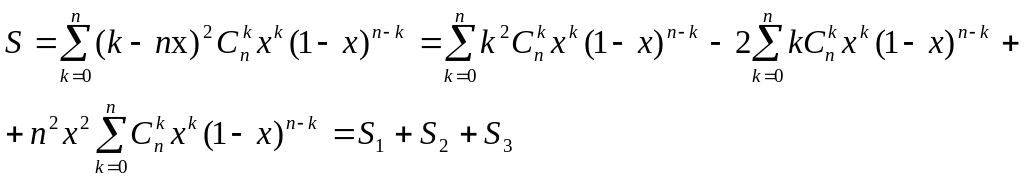
Згідно Леми1:

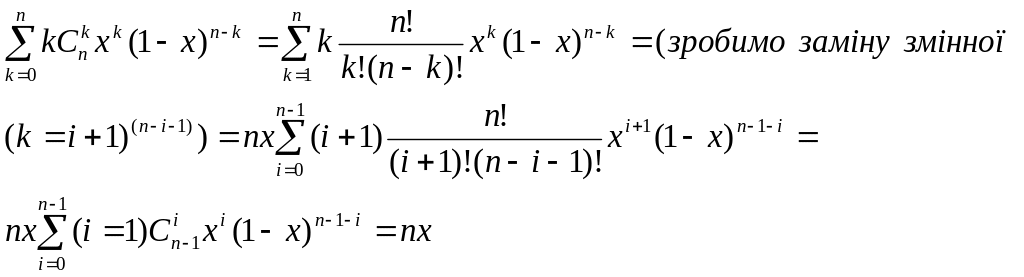
Тоді:

Далі:

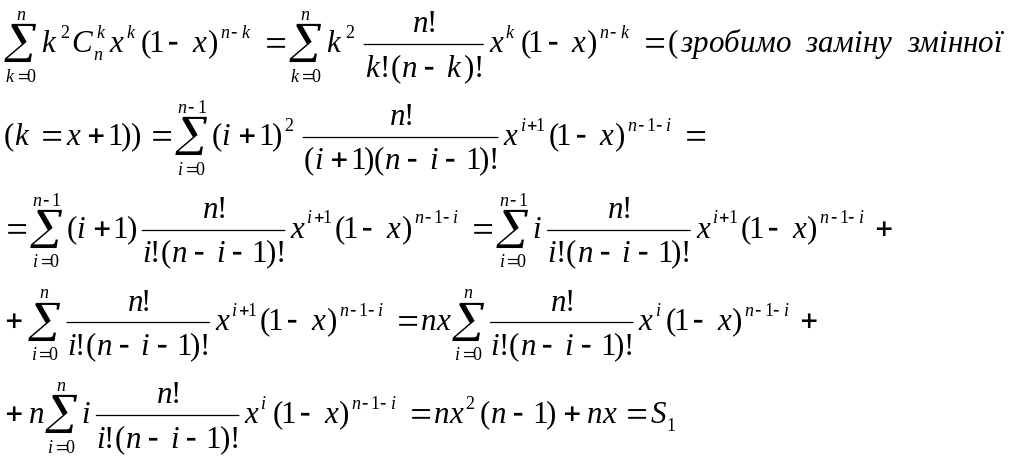
Тоді

Теорема: Нехай f(x) неперервна на [a,b], тоді для  >0, існує :

Доведення Теореми

Будемо вважати, що [а,в]=[0,1], бо можна це завжди досягнути шляхом заміни змінної.

Розглянемо многочлен Бернштейна:

(1)

Покажемо, що при великих n він задовольняє умови теореми.

(2)

Віднімемо від (1) - (2) матимемо:

(3)

Якщо f(x) неперервна на [0,1], то вона рівномірно неперервна, тобто:

ε>0  :  є[0,1]:

ε

Візьмемо  х є[0,1]. Суму в (3) розіб‘ємо на дві:

де сумуємо по тих k для яких і

де сумуємо по тих k для яких

Позначимо через , тоді оцінимо суму

Згідно з Лемою2 при х є[0,1]:

, бо , ,

тоді якщо , то , тоді

Тоді:

Для :

Візьмемо такий, що , тоді

#

Зауваження: Справедливе твердження: Якщо f(x)є[0,1] має неперервну похідну до енного порядку включно, то:

§22. Тригонометричні многочлени найкращого наближення.

Означення: Тригонометричний многочлен порядку n наз. вираз:

Теорема: (ІІ Теорема Веєрштраса): Якщо f(x) неперервна, періодична з періодом , то має місце:

Лема: Нехай неперервна на , тоді парний тригонометричний поліном , такий що:

Доведення Леми:

Заміна , тоді:

є неперервна на [-1;1].

Згідно теореми Веєрштраса §21 існує таке що

, але

Доводиться з використанням формул Ейлера:

Доведення теореми:

Розглянемо парні періодичні функції:

Згідно Леми існують парні тригонометричні многочлени

;

(1)

(2)

В силу парності нерівності (1) (2) справедливі для , а в силу періодичності на всій числовій осі, тому:

(3)

+

(4)

де

Нерівність (3) (4) домножимо на і sinxі додамо їх:

(5)

Розглянемо функцію

Згідно доведеного існує

(6)

Заміна:

тоді з (6)

(7)

де ,

Додавши (5) і (7):

(8)

Тобто: ,

§23. Побудова алгебраїчних многочленів найкращого наближення.

Теорема Веєрштраса вказує що найкраще наближення існує, але не дає практичного способу побудови.

Ефективних способів точної побудови многочлена найкращого наближення до даної функції не існує. Тому розглянемо чисельні методи розв‘язку цієї задачі.

Зробимо деякі розрахунки які покажуть нам алгоритм побудови многочлена найкращого наближення.

І. Нехай на (а, b) задана неперервна f(x) і т утворюють Чебишевський альтернант.

Зайдемо вираз для: через значення функції в т згаданого альтернанту.

Нехай - многочлен найкращого наближення для , тоді:

(1)

де:

Розглянемо детермінант

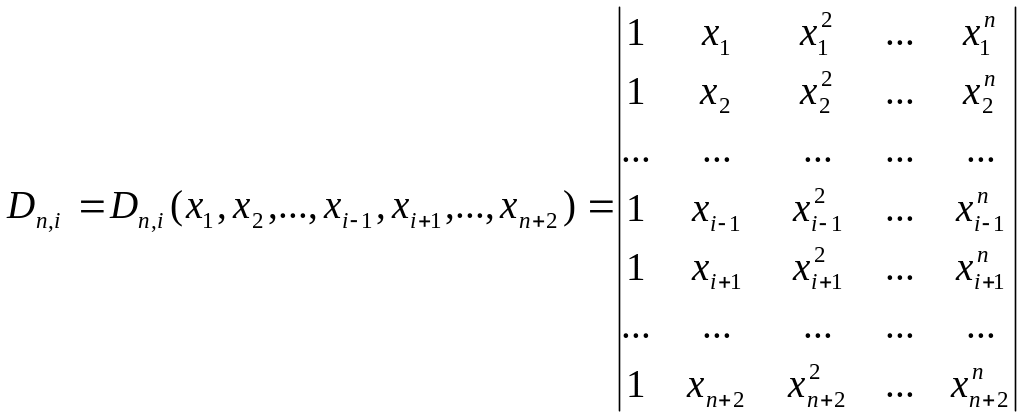
(2)

Усі детермінанти додатні бо . Крім того справедлива рівність:

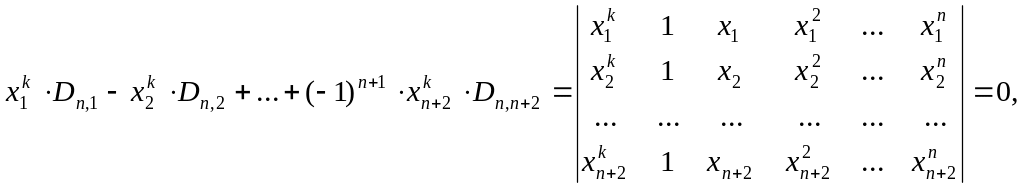
(3)

Рівність і просумуємо по

(4)

Розглянемо ліву частину (4), маємо що

(5)

Введемо позначення:

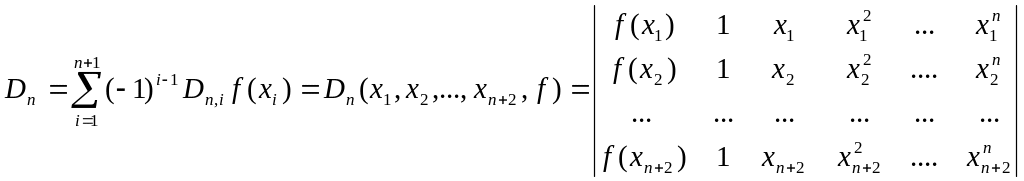
З (3) і останнього виразу (6) маємо:

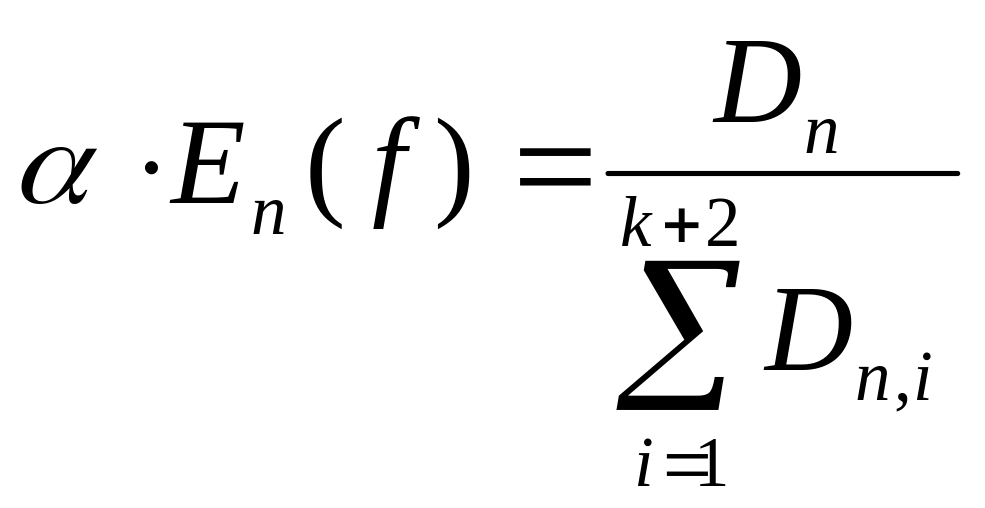(7)

ІІ. Нехай для довільної т. що

Покажемо, що:

1) (8)

де:

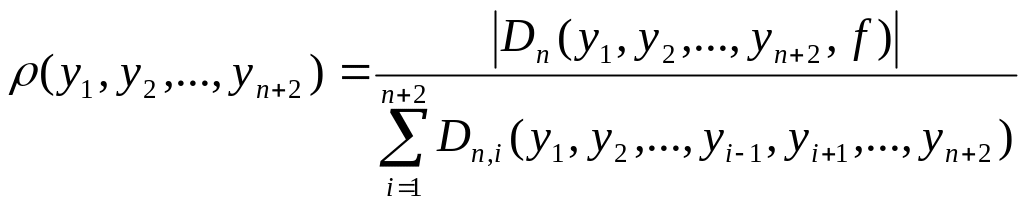
де: і визначається за (6) і (2).

2) Існує т (9)

3) т утворюють Чебишевський альтернанс а отже,:

(10)

де: - многочлен найкращого наближення

Позначимо многочлен який найкраще наближає в точках

- найкраще наближення в т

Нехай - Чебишевський альтернанс для , тоді:

тобто:

Якщо система точок є Чебишевський альтернанс то: , а так як згідно теореми про існування найкращого наближення і Т. Чебишева цей альтернанс завжди існує, то досягає верхньої межі на довільному з цих альтернантів.

Нехай - множина точок

Нехай і - многочлени найкращого наближення для і на множині відповідно.

Аналогічно і - найкраще наближення на і відповідно, тоді:

Оскільки , то:

Множина точок є альтернанс до а отже, має місце (10)

ІІІ. Алгоритм побудови многочлена найкращого наближення до

1) Беремо на систему точок:

2) Нехай , тоді обчислюємо наступні величини

а) 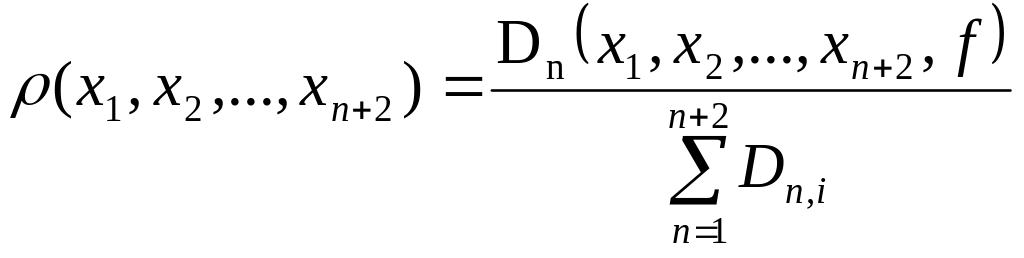використовуючи (2), (6), (7), тоді

, - найкраще наближення f на множині точок

Знаючи знак детермінанта визначаємо знак різниці:

Користуючись рівністю

б) Визначивши систему запишемо рівність:

, (11)

де: , якщо

, якщо

в) Розв‘язуємо систему і знаходимо:

(12)

тобто знаходимо значення многочлена в т .

2) Знаходимо за інтерполяційними формулами в точці. Зайву точку можна використати для контролю бо інтерполяційний многочлен в цій точці повинен набувати наперед задане значення.

3) Якщо , то шукаємо всі можливі комбінації з по . Для кожної з них знаходимо: . Серед вибираємо найбільше знайдене значення і переходимо до пункту 2.

Зауваження: 1) Описаний алгоритм не є єдиний.

2) Можна довести що описаний процес рівномірно збігається до многочлена найкращого наближення.

3) Для збільшення точності потрібно збільшувати кількість точок поділу відрізка .

Приклад:

Для серед всіх многочленів 2-го порядку знайти многочлен найкращого наближення на [-1;1]

m=n+2=4

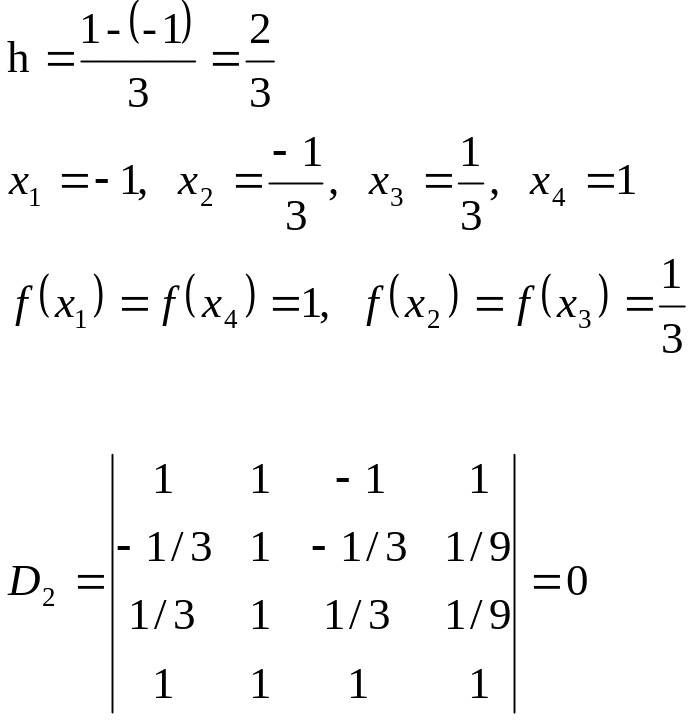
Запишемо систему рівнянь виду (11)

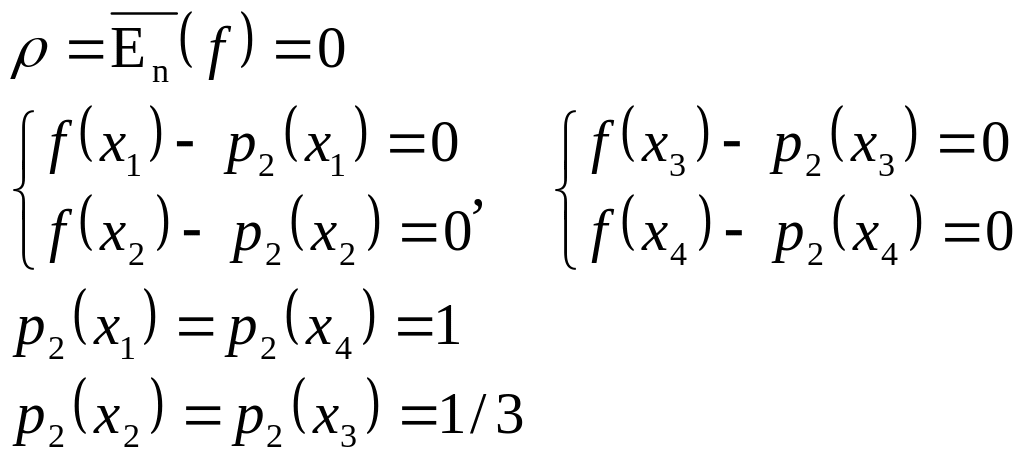
Візьмемо точки

Запишеться інтерполяційний многочлен Лагранжа так: