N. 2 дискретне середньоквадратичне наближення.

Нехай функція задана своїми значеннями в точках . Зауважимо, що ввівши змінну ми згадану систему точок переведемо в точки . Тому . Скалярний добуток означимо так: . В якості лінійно-незалежної системи функцій візьмемо многочлен Чебишева дискретного аргументу: . Дані многочлени будуть ортогональними, тобто

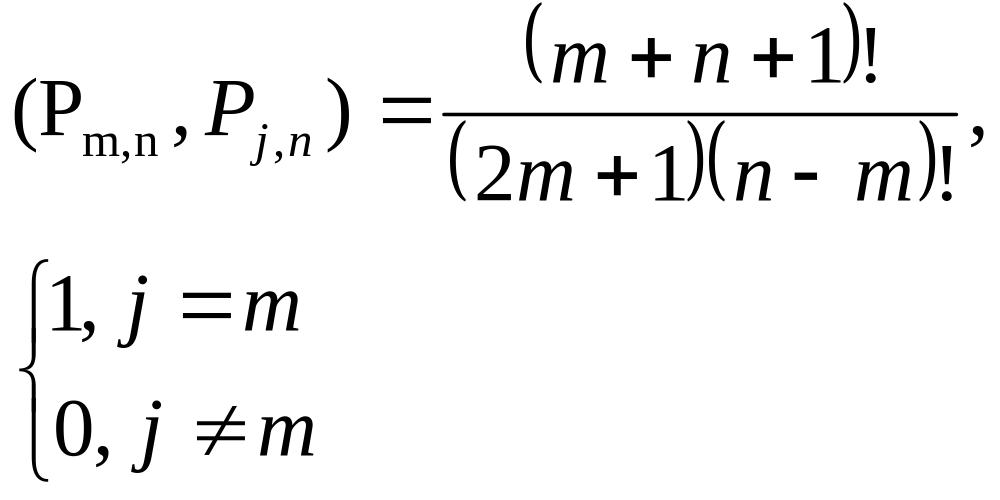
Многочлен найкращого наближення шукаємо у вигляді:

. Відповідно до загальної теорії для знаходження цього многочлена потрібно розв’язати систему: .

З врахуванням ортогональності

N.3 середньоквадратичне наближення тригонометричними многочленами.

Розглянемо простір функцій сумовних з квадратом на відрізку . Елемент найкращого наближення будемо шукати серед: - тригонометричний многочлен степеня . В якості лінійно-незалежної системи функцій беремо ортонормовану систему Розв’язавши систему (2) попереднього параграфа, отримаємо: , , . Тобто найкраще середньоквадратичне наближення для періодичної функції будуть давати частинні суми ряду Фур’є функції

§21

Найкраще рівномірне наближення. Теорема чебишева

Якщо норма в лінійному просторі визначена не через скалярний добуток, то пошук елемента найкращого наближення ускладнюється.

Нехай - множина многочленів степеня не вище . Нехай також функція неперервна на і візьмемо . Відхилення функції від множини означається рівністю , нижню межу величини по всіх многочленах називають найменшим відхиленням.

Критерій за яким визначають елемент найкращого наближення дає теорема.

Теорема Чебишева: нехай неперервна на . Для того щоб степеня не вище був многочлен найкращого рівномірного наближення для функції необхідно і достатньо щоб на відрізку існувала хоча б одна система з -х точок в якій різниця задовольняла б наступні умови:

• Почергово змінює знак

• Набуває найбільшого по модулю значення на .

Ці дві умови можна записати так:

Означення: система про яку їде мова в теоремі називається чебишевським альтернантом.

Означення: точка , або 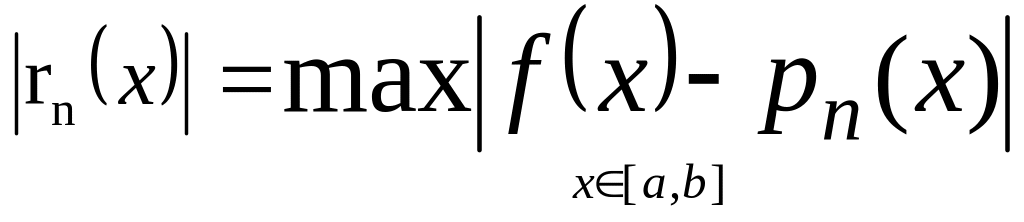називатимемо е-точкою.

Означення: якщо в е-точці виконується , то точку називають “+” точкою, а якщо , то “-” точкою.

Доведення

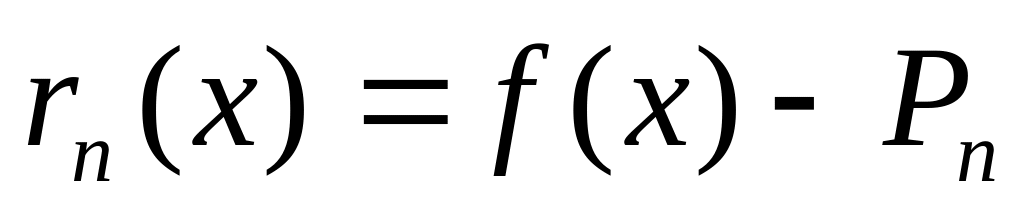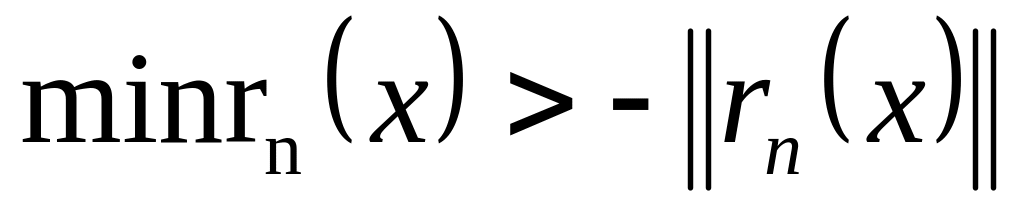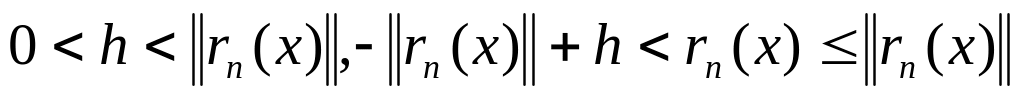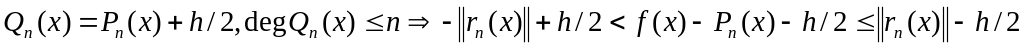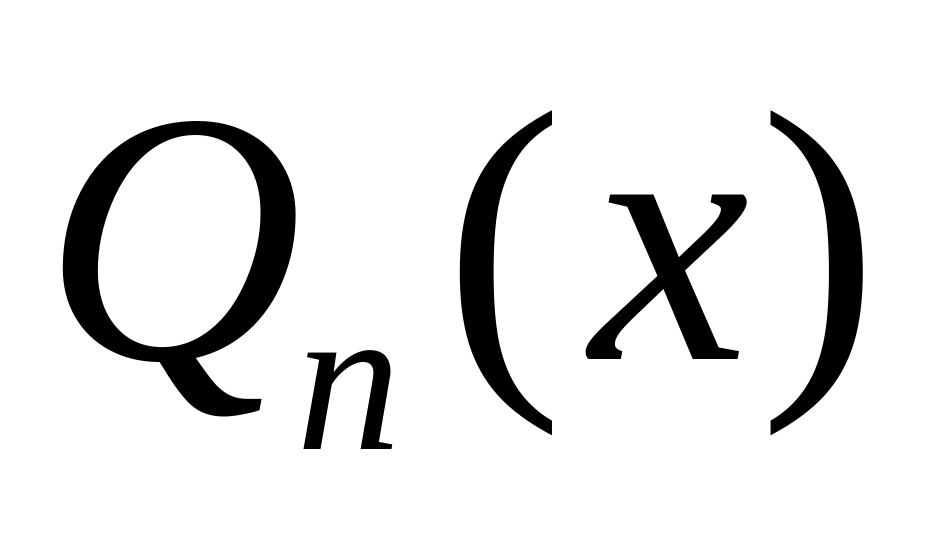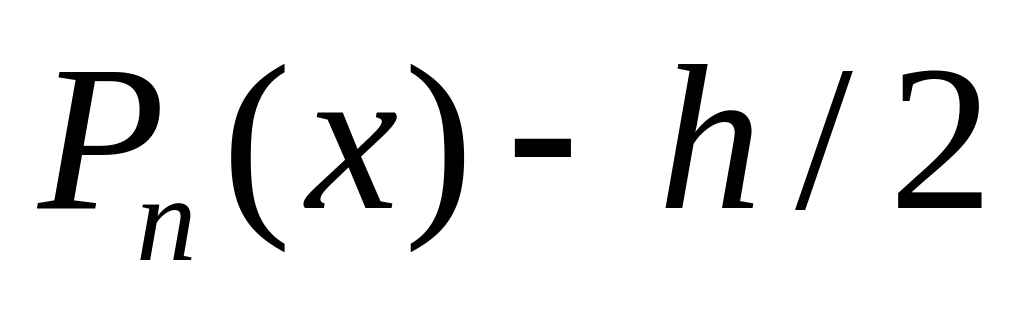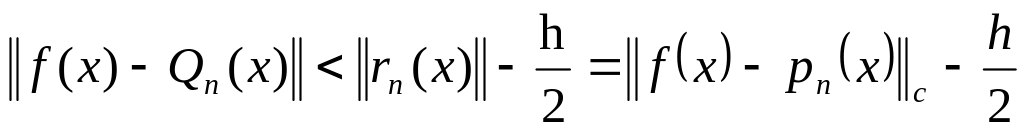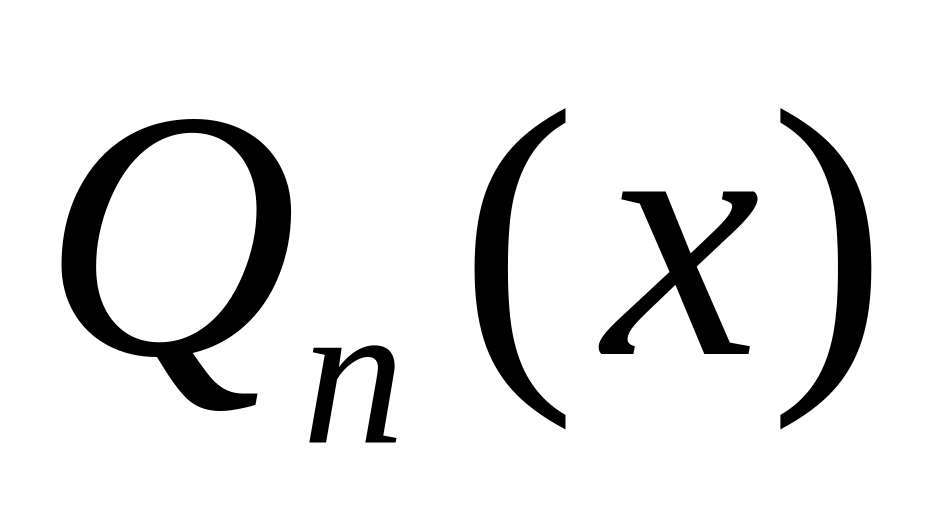1. покажемо, що на існують – і + точки. Оскільки є функція неперервна на , то існують е-точки. Нехай наприклад не існує – точок, тоді існує (1). Позначимо , позначимо через = ,тобто , тому многочлен дає краще наближення ніж 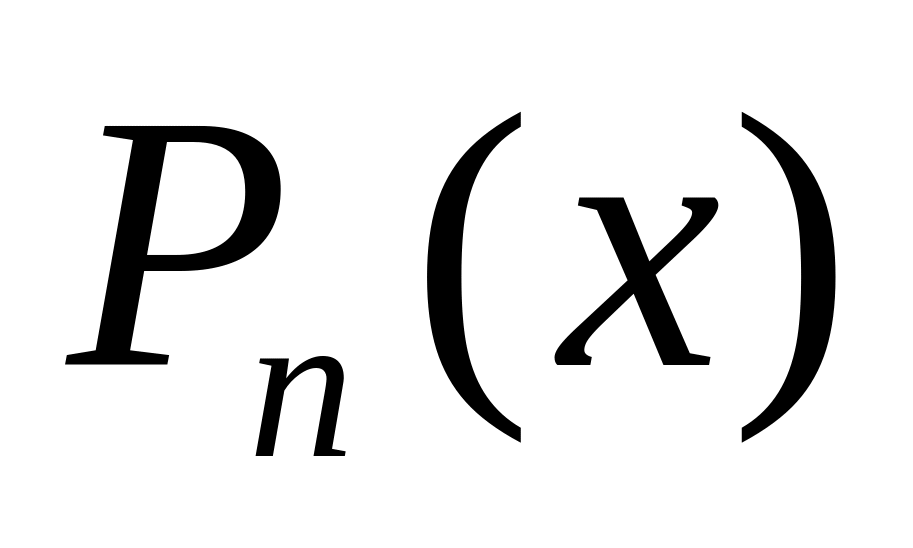. Отримана суперечність “-”і “+” точки існують.

2. покажемо, що відрізок можна розбити на 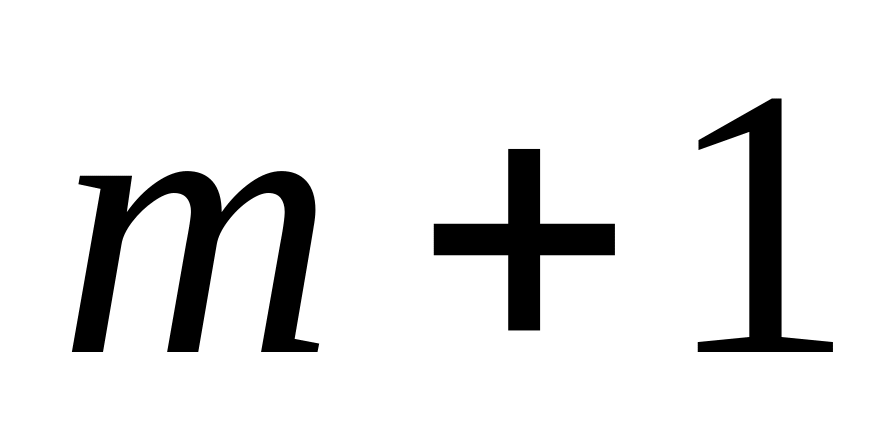відрізок точками 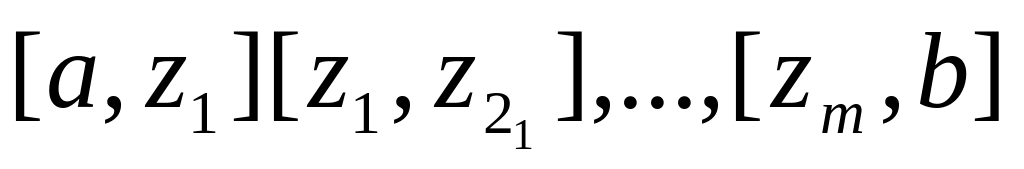, так щоб кожен з отриманих відрізків містив лише “-“ або “+” точки. Нехай перша е-точка справа від а це “+” точка, тоді через 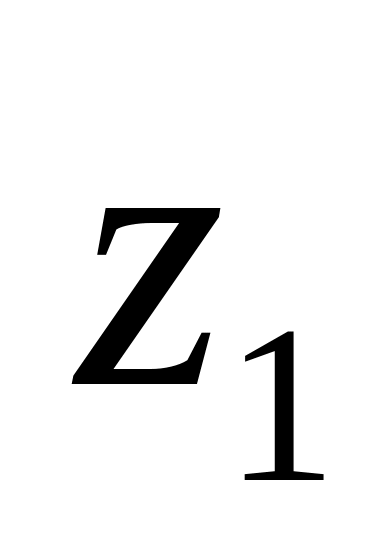позначимо самий правий нуль величини 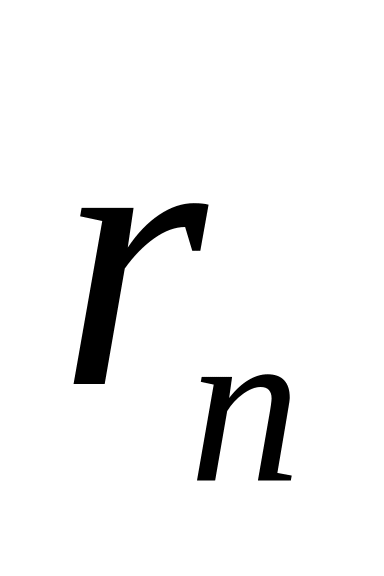між точкою а та першою після неї “-” точкою. - самий правий нуль величини між точкою і першою після неї нуль точкою.

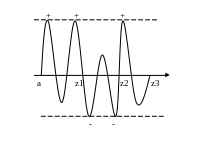
3. покажемо, що 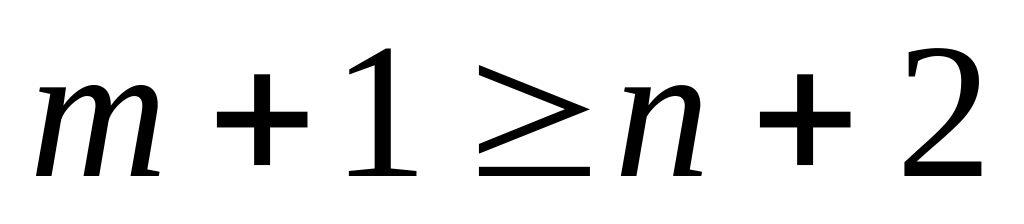. Припустимо протилежне 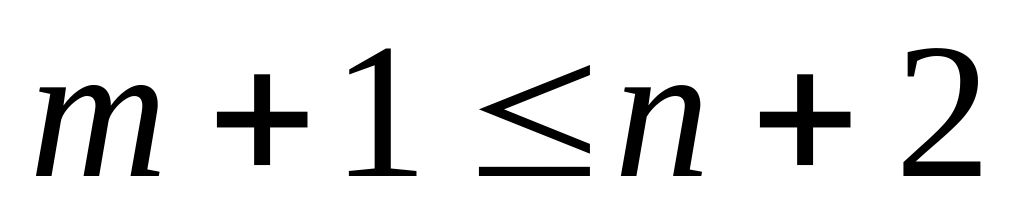, тобто 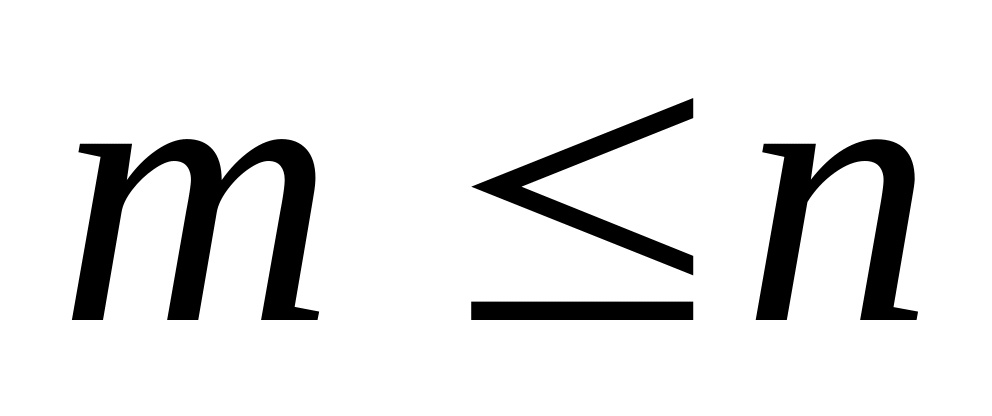. На відрізку 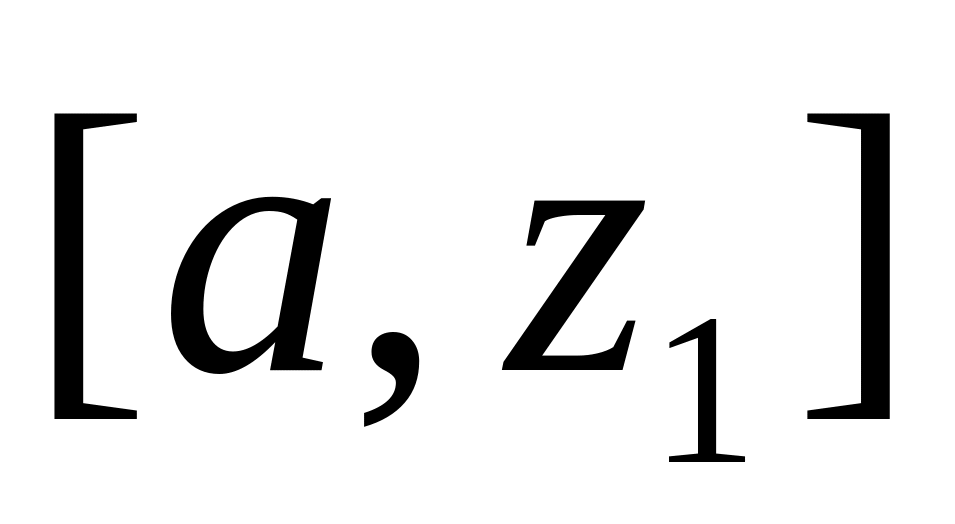не має “-” точок на 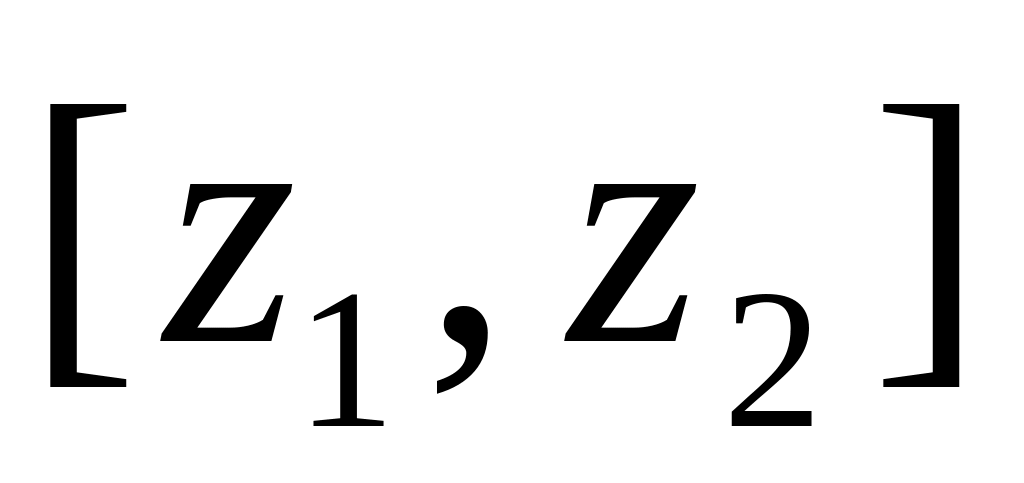не має “+” точок ... , тому існує число 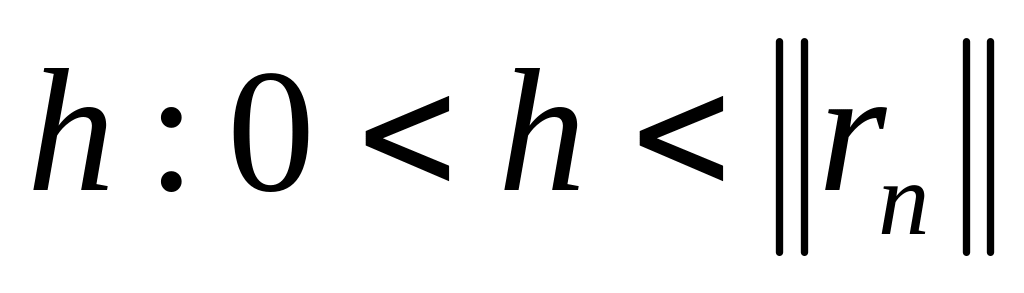і таке, що 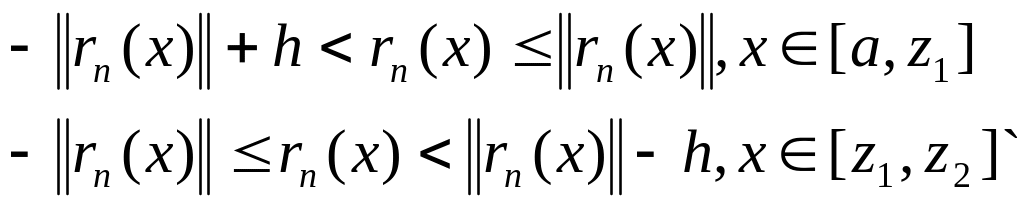(2)

де підберемо так щоб

має той самий знак що й

позначимо , якщо , якщо крім того враховується нерівність (2), то , аналогічно таким чином многочлен дає краще наближення ніж . Отримана суперечність доводить необхідність.

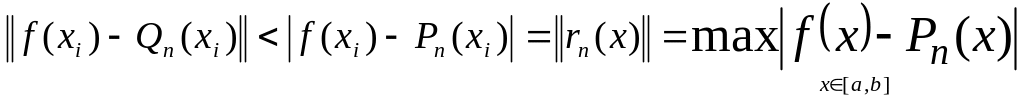2. нехай многочлен такий, що для нього виконуються умови 1 і 2 теореми. Доведемо, що він є многочленом найкращого наближення. Припустимо протилежне. Нехай , тому в усіх точках : , тому в усіх точках різниця , має той самий знак, що і , тобто ця різниця змінює знак хоча б n+2 рази, тобто різниця , степінь якої , має не менше n+1 коренів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.

Теорема Чебишева: нехай на дійсній осі задано 2п періодична функція. Для того, щоб тригонометричний поліном порядку не вище n був многочленом найкращого наближення для .необхідно і достатньо щоб на існувала хоча б одна система з 2n+2 точок в яких різниця задовольняє умову: .

§21