Наближення функцій в лінійному нормованому просторі. Умови існування та єдності елемента найкращого наближення.

Нехай - лінійний нормований простір, , -лінійно-незалежні елементи. Через позначимо лінійний підпростір узагальнених многочленів виду , де . Множина , де , обмежена знизу наприклад нулем. Тому існує - найкраще наближення. Виникає питання чи в множині існує елемент : (*). Якщо такий елемент існує, то його називають елементом найкращого наближення функції многочленами з множини .

Означення: довільний елемент для якого виконується умова (*) називається елементом найкращого наближення для функції

Теорема 1: Для в множині існує елемент найкращого наближення, множина таких елементів опукла.

Зауваження: елемент найкращого наближення не обов’язково один. Наприклад, розглянемо простір векторів з нормою . Візьмемо точку і візьмемо одновимірний підпростір з базисними векторами . Очевидно, що 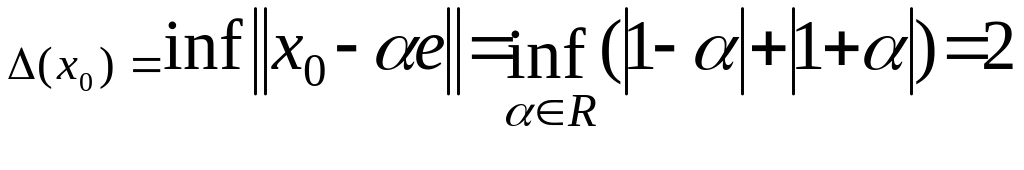при . Таким чином маєм нескінченну множину елементів найкращого наближення.

Теорема 2: Якщо простір строго – нормований, то елемент найкращого наближення єдиний.

Теорема 3: (характеристика елемента найкращого наближення) Якщо в множині існує елемент - елемент найкращого наближення для функції , то тоді для .

Теорема 4: Якщо : , то - елемент найкращого наближення для функції f многочленна М.

Як побудувати елемент найкращого наближення в просторі з скалярним добутком?

Нехай , - лінійно-незалежні елементи. Комбінації утворюють лінійний простір. Якщо деякий елемент є елементом найкращого наближення для функції , то згідно з теоремою 3 різниця ортогональна до всіх елементів підпростору , в тому числі й до елементів , . Тобто (1) для . Оскільки елемент найкращого наближення існує, то система (1) має розв’язок. Користуючись теоремою 4 можна довести, що розв’язок системи (1) є елементом найкращого наближення функції . Методом від супротивного можна довести, що такий елемент єдиний. Таким чином в просторі з скалярним добутком відшукання елемента найкращого наближення виду зводиться до розв’язання системи лінійних алгебраїчних рівнянь (1), яку зручніше записати у вигляді: , . (2)

§19

Середньоквадратичне наближення функцій.

N.1 НАБЛИЖЕННЯ АЛГЕБРАЇЧНИМИ МНОГОЧЛЕНАМИ.

Візьмемо метричний простір функцій сумовних з квадратом, тобто функцій для яких виконується умова .

Для довільних функцій скалярний добуток задамо так: . Легко перевірити, що всі аксіоми скалярного добутку тут виконуються, якщо дві функції, які відрізняються на множині міри нуль вважати рівними.

Означення: Найкраще наближення в просторі називається найкращим середньоквадратичним наближенням або наближенням за методом найменших квадратів.

В якості лінійно-незалежної системи візьмемо функції: , елемент найкращого наближення будемо шукати в множині многочленів виду: . Виходячи з загальної теорії стверджуємо, що многочлен найкращого наближення існує, для його побудови потрібно знайти розв’язок системи (2) з попереднього параграфа, вважаючи, що , .

Таким чином маємо систему з рівнянь:

;

; (1)

.....................................................................

.