Кусково-кубічна сплайн інтерполяція.

Означення: Сплайном називається функція для якої існує поділ її області визначення на підобласті, такі що в середині кожної підобласті ця функція є многочленом деякого степеня . Крім того ця функція неперервна на області визначення разом зі своїми похідними до порядку.

Найчастіше використовують випадок . Нехай на задана неперервна функція , задане розбиття відрізка точками: , для всіх .

Кубічним сплайном, який наближає дану функцію будемо називати функцію , яка задовольняє наступні умови:

а) на кожному з відрізків ;

б) , , ;

в) для всіх .

Доведемо існування та єдність такого сплайну. Доведення носитиме конструктивний характер, тобто буде містити спосіб побудови сплайна. Будемо позначати через ту частину сплайна, яка відповідає відрізку , , р(х)= , де ,(1) де - коефіцієнти, які потрібно знайти.

,

.

З умови в) випливає .(2)

З того, що .

В (1) підставивши, отримаємо:

.

Позначимо .

З останньої рівності будемо мати: .(3)

З того, що ,

, , (4) .

З того, що .

Тобто , , (5) .

Об’єднуючи (3), (4) і (5) отримаємо систему рівняння з невідомими. Ще два рівняння дістанемо, якщо задамо деякі крайові умови для сплайна . Наприклад: , тобто або , .

З рівнянь (3), (4), (5) виключимо коефіцієнти . Отримаємо деяку систему рівнянь, яка містить коефіцієнти .

З (3) , (*)

.

Віднімемо дані рівності, і підставимо в (4), отримаємо: .

Звівши подібні доданки, отримаємо:

.(6)

З рівності (5) маємо: , . Підставимо дані рівності в (6), отримаємо: . Позбудемось індексу ( ): , (7) , , .

Дана система має єдиний розв’язок. Розв’язавши одним з відомих методів систему (7) коефіцієнти шукаємо з (5) і (*).

(8)

(9)

Зауваження: ми вибирали граничні умови , але в загальному випадку їх слід вибирати з властивостей функції, яку наближаємо.

Наприклад: нехай відомі , , то покладаємо , .

Якщо в вузлах інтерполяції функція, яку наближаємо задана не точно, а наближено, то немає смислу будувати сплайн, який в точках набував би значення . Будують сплайн, який в точках проходить поблизу заданих значень . Такий процес називають сплайн-інтерполяцією з вирівнюванням.

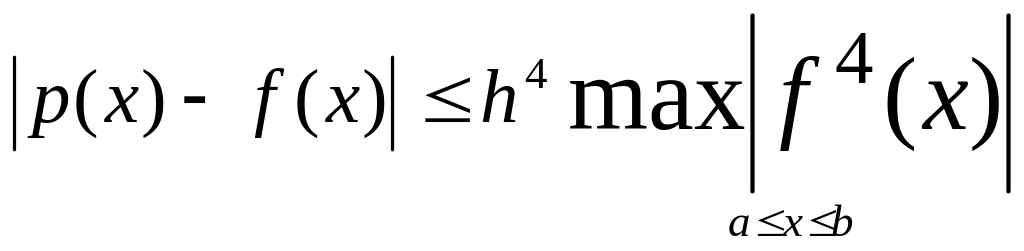
§16

Деякі відомості про різницеві рівняння. Означення: Різницевим рівнянням називається рівняння відносно функції дискретної змінної.

Розглянемо найпростіший випадок одного лінійного рівняння відносно невідомої функції одного цілочисельного аргументу.

(1)

Відмітимо, що це рівняння називається лінійним різницевим рівнянням к-того порядку. Воно є дискретним аналогом лінійного диференціального рівняння порядку k рівняння: .

Означення: Рівняння (2) називається лінійним однорідним різницевим рівнянням.

Теорема: Якщо є деякий частинний розв’язок рівняння (1), то є розв’язком однорідного рівняння (2).

Означення: Система розв’язок рівняння (2) називається лінійно незалежною, якщо з того, що

Теорема: Якщо деякі функції є розв’язком однорідного рівняння (2), то лінійна комбінація теж є розв’язком рівняння (2)

Мають місце наступні твердження:

1. Загальний розв’язок неоднорідного рівняння дорівнює сумі його частинного розв’язку і загального розв’язку відповідного однорідного рівняння.

2. Якщо функції є розв’язками однорідного рівняння (2), то теж є розв’ язком рівняння (2).

3. Якщо 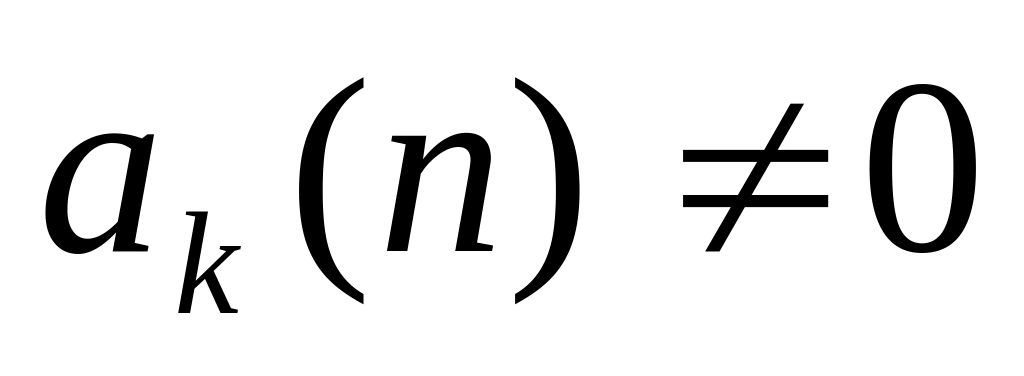, то загальний розв’ язок рівняння (2) можна записати у вигляді: 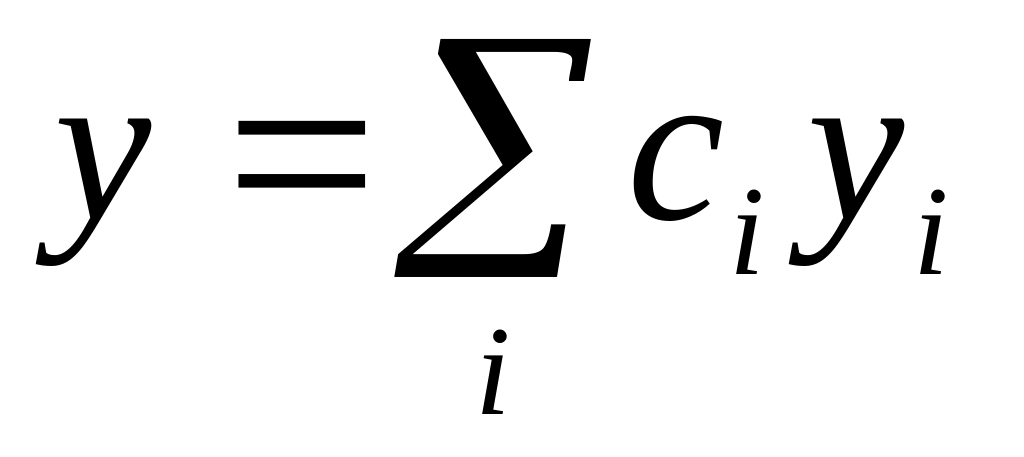, де - лінійно-незалежні розв’ язки рівняння (2).

Означення: Якщо в рівняннях (1) і (2) коефіцієнти не залежать від , то такі рівняння називаються рівняннями з сталими коефіцієнтами.

( )

( )

розв’ язок рівняння (2) будемо шукати у вигляді: . Тобто .

Бачимо, що кожному кореню рівняння відповідає частинний розв’ язок рівняння ( ), а саме . Якщо всі корені характеристичного рівняння прості, то маємо к-різних розв’язків. Якщо деякий корінь має кратність , то йому відповідають розв’язки: , , …, .

§17

МНОГОЧЛЕНИ ЧЕБИШЕВА.

- позначаються, . Задаються наступними рівностями: , , . (1) Використовуючи рекурентні формули (1), отримаємо: , .

Відмітимо, що коефіцієнт біля в многочлена дорівнює , всі многочлени з індексами - парні, з індексами - непарні.

Відомо, що ,

Позначимо .

Отримаємо: .(2)

Порівнюючи (1) і (2) бачимо, що функція задовольняє рекурентне співвідношення (1). Початкові умови: , . Таким чином:

(3). З даної рівності випливає, що при . (4)

Зауваження: нерівність (4) не буде справедливою при всіх . Якщо , то , а такого числа не завжди менше 1.

Рекурентне співвідношення (1) є різницевим рівнянням. Позначимо , тоді отримаємо характеристичне рівняння:

Якщо , то корені прості, а тому . Замість підставимо 1, отримаємо: або .

Тому . (5) – многочлен Чебишева

Зауваження: з нерівностей (4) випливає, що многочлени Чебишева набувають значення тоді, коли , , , , де .

Означення: Многочлен називають многочленом, який найменше відхиляється від нуля. Таке означення пояснюється наступною теоремою:

Теорема: Якщо з старшим коефіцієнтом рівним одиниці, то .

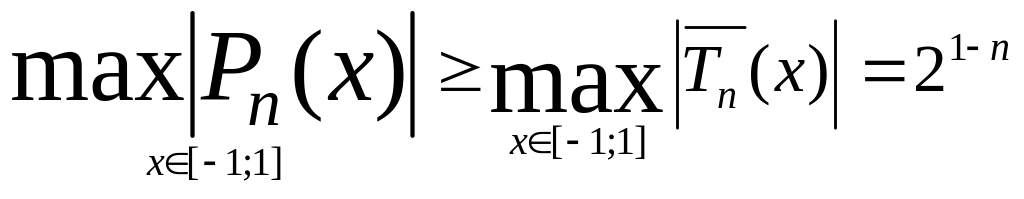Теорема доводиться методом від супротивного .

Заміною змінної проміжок переводимо взаємно однозначно в проміжок . Тоді многочлен з старшим коефіцієнтом називається многочленом Чебишева на . Аналогічно як ми робили для , можна побудувати многочлен, який найменше відхиляється на .

Цей многочлен запишеться:

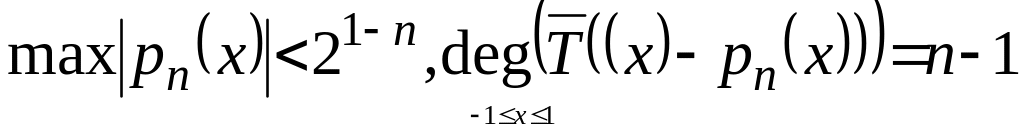
Розглянемо значення многочленна

Отримали, що многочлен степеня n-1 має n нулів, що суперечить основній теоремі алгебри. Отримана суперечність доводить теорему.

§18