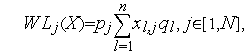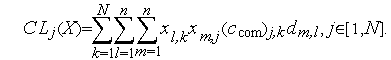Операционные системы параллельных вычислительных систем. Планирование процессов

1. Задача оптимального отображения параллельных процессов на архитектуру многопроцессорной вычислительной системы

2. Операционные системы мультипроцессоров. Планирование процессов

3. Операционные системы мультикомпьютеров. Планирование процессов

4. Операционные системы мультикомпьютеров. Спектральный алгоритм балансировки загрузки

5. Отображение процессов с регулярной структурой на типовые архитектуры мультикомпьютеров

Задача оптимального отображения параллельных процессов на архитектуру многопроцессорной вычислительной системы

Важнейшей функцией операционной системы МВС является функция планирования процессов. Задача планирования процессов является частью задачи оптимального отображения параллельных процессов на архитектуру многопроцессорной вычислительной системы (mapping).

Задача оптимального отображения.

Пусть   - граф некоторой прикладной задачи (точнее, используемого алгоритма решения этой задачи). Здесь   - вершины графа, отождествляемые с процессами,   - ребра графа, отождествляемые с информационными связями между процессами:   - процессы  связаны информационно (точнее – процесс   передает информацию процессу  ). Обозначим   вычислительные сложности процессов  , соответственно;   - количество информации в байтах, которое процесс   передает процессу  .

Положим, что имеется многопроцессорная вычислительная система с универсальными процессорами, каждый из которых может выполнить любой из процессов  . Пусть   - граф (возможно, циклический) данной МВС. Здесь   - вершины графа, соответствующие процессорам,   - ребра графа, отождествляемые с коммуникационной сетью:  =1 означает, что имеется возможность прямой передачи данных от процессора   процессору  ;  =0 - такой возможности нет. Производительности процессоров   обозначим  , ,..., , соответственно. Связь   будем описывать двумя величинами:

 - латентность канала связи - время, необходимое для организации передачи данных от процессора   процессору  ;

 - величина, обратная пропускной способности канала связи - время, необходимое для передачи байта данных от процессора   процессору   (без учета времени  ).

Задачей оптимального отображения параллельных процессов   на процессоры   называется задача оптимального отображения графа   на граф   - задача поиска такого распределения процессов   по процессорам  , которое минимизирует некоторый критерий оптимальности (обычно время вычислений).

Введем в рассмотрение ( * ) отображающую матрицу

 - процесс   назначен на выполнение процессору  ;

 - процесс   не назначен на выполнение процессору  .

Заметим, что отображающая матрица   не выполняет отображение дуг   графа   на дуги   графа  .

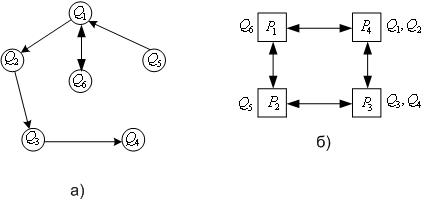
Рассмотрим в качестве примера отображение графа   на граф   (см. рис. 1).

Рис. 1.  а) Топология информационных связей процессов Q={Q₁,...,Q₆} в графе (Q,D). б) Коммуникационная сеть процессоров P={P₁,...,P₄} в графе (P,C) и отображение процессов Q={Q₁,...,Q₆} на эту сеть.

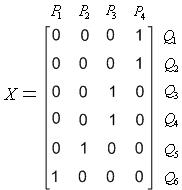
Отображению процессов   на сеть процессоров  , приведенное на рис. 1 выполнено с помощью отображающей матрицы

Рис. 2.  

Во введенных обозначениях задачу оптимального отображения графа   на граф   можно формализовать следующим образом: найти отображающую матрицу   такую, что

(1)

Здесь   – критерий оптимальности, { } - множество допустимых отображений. Матрицу   будем называть оптимальной отображающей матрицей.

Если в процессе вычислений процессы   выполняются многократно и вычислительная сложность их меняется от итерации к итерации, то статическое отображение параллельных процессов на архитектуру многопроцессорной вычислительной системы может быть неэффективно. В этом случае задачуотображения приходится решать многократно в ходе итераций, т.е. использовать динамическое отображение параллельных процессов на архитектуру многопроцессорной вычислительной системы .

Как всякая задача отображения графа на граф, задача оптимального отображения является  -сложной. Отсюда следует, что принципиально не существует универсальных методов решения этой задачи.

Балансировки загрузки.

Одним из распространенных способов приближенного решения задачи оптимального отображения является метод балансировки загрузки многопроцессорной вычислительной системы. Основная идея метода балансировки загрузки состоит в распределении процессов по процессорам таким образом, чтобы суммарная вычислительная и коммуникационная загрузки процессоров были примерно одинаковы. При этом не учитываются коммуникационные загрузки процессоров, обусловленные транзитными обменами, конфликты при обменах вследствие перегрузки коммуникационной сети, времена на организацию обменов  .

Назовем вычислительной загрузкой процессора   величину

(2)

а его коммуникационной загрузкой – величину

(3)

Тогда задачу балансировки загрузки можно записать в виде

(4)

Минимаксная задача (1), (4) формализует, в частности, компромисс между двумя следующими тенденциями. С одной стороны, увеличение числа процессоров, между которыми распределены вычисления, уменьшает общее время решения задачи (до некоторого числа процессоров). С другой стороны, распределение вычислений между многими процессорами увеличивает коммуникационные расходы, что увеличивает общее время решения задачи.

В общей постановке задача (1), (4) является  -сложной задачей целочисленного нелинейного программирования. Однако хорошие приближенные методы решения этой задачи (особенно без учета коммуникационной загрузки процессоров) разработать проще.

В некоторых случаях задача (1), (4) может быть решена точно. Например, если граф   представляет собой двухмерную регулярную решетку и вычислительные и коммуникационные сложности процессов   постоянны и одинаковы, то оптимальным является разрезание этой решетки на  одинаковых полос (по числу процессоров в системе) и назначение каждой из этих полос своему процессору. Подобная ситуация может иметь место при решении краевых задач для ДУЧП методом конечных разностей.

Заметим, что задачи балансировки загрузки может быть поставлена не только в терминах математического программирования, но и в других терминах. Например, в терминах теории графов задача может быть сформулирована следующим образом: разрезать граф   на   частей так, чтобы суммарный вес разрезанных ребер был минимальным, а суммарные веса вершин, входящих в разрезанные части, примерно равны. Если в графе   имеет место передача большого количества коротких сообщений, то вместо суммарного веса разрезанных ребер следует минимизировать число разрезанных ребер, поскольку основное время при передаче короткого сообщения тратится на инициализацию самого процесса передачи данных.

Отметим особую актуальность балансировки загрузки при решении задач на нерегулярных сетках.

Если в процессе вычислений процессы   выполняются многократно и вычислительная сложность их меняется от итерации к итерации, то статическая балансировка загрузки может быть неэффективной. В этом случае задачу приходится использовать динамическую балансировку загрузки.

Примером задач, для которых статическая балансировка загрузки неэффективна, являются задачи моделирования горения с помощью разностных схем. Время обработки узлов сетки, в которых интенсивно протекают химические реакции (эти точки расположены на фронте пламени), значительно превышает время обработки узлов сетки, в которых горения не происходит. Если используемая конечно-разностная сетка разрезана на равные полосы по числу процессоров в системе, то узлы сетки, которые захвачены фронтом горения, могут оказаться локализованными на небольшом числе процессоров и несбалансированность загрузки процессоров может быть очень велика. Для балансировки загрузки процессоров в этом случае необходимо перераспределять "горячие" узлы сетки между всеми процессорами. Поскольку фронт пламени смещается в ходе решения задачи, статически это сделать невозможно. В то же время динамическое перераспределение узлов сетки может дать хорошие результаты.

Методы динамической балансировки загрузки различаются тем,

• когда процессоры обмениваются информацией о своей текущей загрузке,

• где принимается решение о перераспределении загрузки,

• когда производится перераспределение загрузки,

• в соответствии с каким алгоритмом происходит перераспределение загрузки.

 Процессоры могут обмениваться информацией о своей текущей загрузке на каждой итерации решения задачи, периодически, когда загрузка процессора станет меньше некоторой допустимой, по появлении свободного процессора, по отторжении процесса процессором вследствие перегрузки и т.д.

 Решение о перераспределении загрузки может приниматься централизованно (на основе глобальной информации о загрузке) и децентрализовано (на основе только локальной информации о загрузке).

 Перераспределение загрузки может происходить синхронно и асинхронно.

 В качестве алгоритмов перераспределения загрузки могут использоваться детерминированные и стохастические алгоритмы, алгоритмы, в которых перераспределение загрузки производится по инициативе получателя и по инициативе отправителя и пр.

Задача балансировки загрузки обычно решается программными средствами, хотя имеются и аппаратные реализации.

Перспективно использование нейронных сетей для решения задач балансировки загрузки.

Заметим, что проблема обеспечения сбалансированной загрузки процессоров в ходе решения задачи является одним из основных препятствий на пути эффективного использования многопроцессорных вычислительных систем. Несмотря на ощутимые успехи в решении задач статической и динамической балансировки загрузки, типичный коэффициент интегральной загрузки большинства систем массового параллелизма составляет по разным оценкам всего от 10% до 3%. И это несмотря на наличие алгоритмов и программ, обеспечивающих весьма высокий (часто более 90%) коэффициент распараллеливания при решении многих задач.