16. Қысқа жол есебі. Дейкстра есебі

Қысқа жол есебі транспорт желісіндегі берілген бастапқы пункт пен көзделген пункт арасындағы қысқа жолды анықтау үшін қолданылады. Мұндай моделдерді сан түрлі жағдайларда қолдануға болады. Енді осы есептің кейбір практикалық жағдайларына тоқталалық.

1-сурет. Жабдықты алмастыру есебі қысқа жол іздеу есебі ретінде

2-сурет. Желілік модель

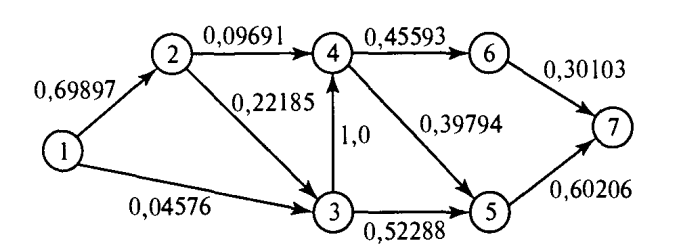
3-сурет. Қысқа жол іздеу есебінің желілік моделі

4-сурет. Үш бидонмен бас қатыру – қысқа жол іздеу есебі.

Қысқа жолды анықтау алгоритмдеріне: Дейкстра, Флойд алгоритмдерін жатқызуға болады.

Дейкстра алгоритмі бастапқы (1-ші) түйін мен кез-келген басқа түйін арасындағы ең қысқа арақашықтықты табуға арналған.Біз i түйінінен j түйініне жету үшін мынадай белгілеулерді қолданамыз: u_i- 1-ші түйіннен i-ші түйінге дейінгі қысқа қашықтық. d_ij- (i, j) қабырғасының ұзындығы болсын делік, онда j түйінінің таңбасы келесідей анықталады:[u_j, i] = [u_i +d_ij, i], d_ij>= 0.Түйін таңбалары екі түрлі болады: уақытша және тұрақты.Уақытша таңбалар одан да қысқа жол табылғанда келесі уақытша таңбаға ауысады. Ең қысқа жол табылғанда уақытша таңба тұрақты таңбаға ауысады.Дейкстра алгоритмі:

0 кезең. Бастапқы 1 түйінге [0, -] таңбасы беріледі. i = 1 делік.

i-ші кезең.а) i түйінінен шығатын барлық уақытша j түйіні үшін [u_i + d_ij, i] таңбасы қарастырылады.Егер j түйінінде k түйінінен алған [u_j, k] таңбасы болса және u_i + d_ij< u_j болса, онда [u_j, k] таңбасы [u_i + d_ij, i] таңбасына ауысады.

б)Егер барлық түйіндер тұрақты болса есептеу тоқтатылады.

1-ші түйін мен кез келген басқа түйін арасындағы жол (маршрут) ең соңғы түйіннен 1 түйінге дейін тұрақты таңбаларды алып тастап отырғанда дұрыс болса, сол жол шешім болады.

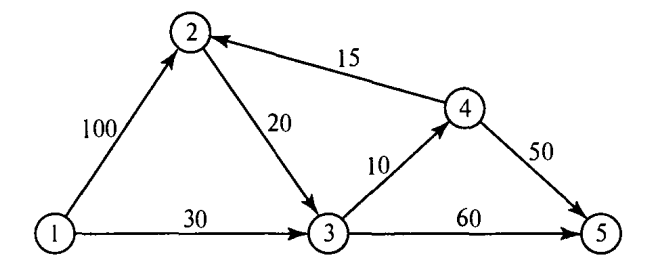
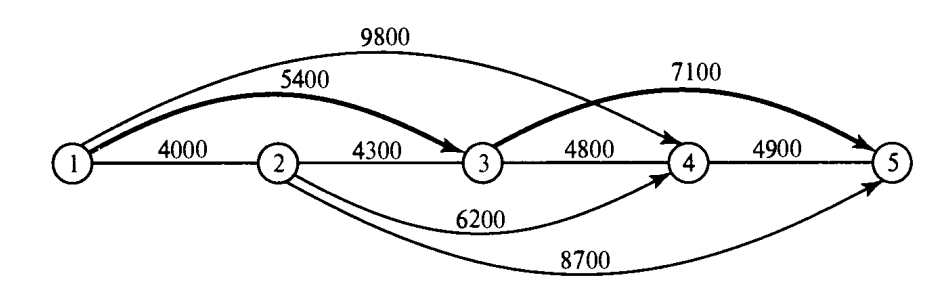
1-сурет. Дейкстра алгоритмі желісінің мысалы.

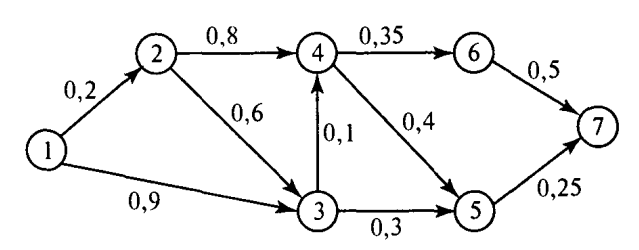
2-сурет. Дейкстра алгоритмін қолдану

16. Желілік моделдер

Желі доғалар немесе қабырғалар арқылы жалғасқан түйіндер жиынынан тұрады. Желіні жиындардың жұбы арқылы өрнектейміз. N – түйіндер жиыны, A - қабырғалар жиыны.

Мысалы, 1-суретте көрсетілген желі төмендегіше өрнектеледі.

N={1,2,3,4,5},

A={(1,2), (1,3), (2,3), (2,5), (3,4), (3,5), (4,2), (4,5)}

Желі мысалы

желінің бұтасы мен діңгектік бұтасы

Минимум діңгектік бұта құру алгоритмі барлық түйіндерді қысқа жолдармен байланыстыруды білдіреді.

Телевизиялық компания өзінің кабелдік желісіне жаңа бес ауданды қосуды жоспарлайды. Жоспарланатын желі мен аудандардың ара қашықтығы 3-суретте көрсетілген.

23. Шекаралар мен тармақтар әдісі

Шекаралар мен тармақтар әдісі – комбинаторика әдістерінің бірі. Оның мағанасы – нұсқаларды белгілі бір тәртіпте сұрыптауды және олардың арасындағы тиімді шешім табуға қандайда бір қесиеттері бойынша пайдалы ларын ғана қарастыруды білдіреді.

Шекаралар мен тармақтар әдісінде бүтін емес ұйғарымды шешімдер жиыны қайбір тәсілмен бірнеше ішкі жиындарға тармақталады да, олардың әрқайсысы үшін бүтін санды шешім алуды көздейтін жаңа сызықтық программалау есебі шығарылады. Әрбір тармақта жаңа екі есеп алынады.Бұл кезеңде төмендегі төрт жағдайдың бірі орын алады.

1. Екі есептің біреуі шешілмейді, ал екіншісі бүтін санды тиімді

жоспарға ие болады. Онда осы жоспар мен ондағы мақсат функциясының мәні бастапқы есептің шешімін береді.

2. Екі есептің біреуі шешілмейді, ал екіншісі бөлшек сандары бар

бүтін санды тиімді жоспарға ие болады. Онда екінші есеп қарастырылады да, оның тиімді жоспарынан мәні бөлшек сан болатын компонентті таңдаймыз. Содан соң осы айнымалының бүтін сандық шешіміне жақындатып алынған жаңа шектеулерге сай екі есеп қрастырамыз.

3. Екі есеп те шешіледі. Оның бірі тиімді бүтін сандық жоспарға ие, ал

екіншісінің тиімді жоспарында бөлшек сандар бар. Онда осы жоспарлардағы мақсат функцияларының мәндерін есептеп, өз-ара салыстырамыз. Анықтық үшін бұдан былай мақсат функциясының минимумы туралы есеп қарастырылады дейік. Егер бүтін сандық жоспардағы мақсат функциясының мәні бөлшек сандары бар жоспардағы мәннен кіші немесе тең болса, онда осы бүтін санды жоспар бастапқы есеп үшін тиімді болады да мақсат функциясының мәнімен қосылып ізделінді шешімді береді. Егер бөлшек сандары бар жоспардағы мақсат функциясының мәні кіші болса, онда сол бөлшек айнымалалардың біріне қатысты тармақтандыру жасап, екі жаңа есеп құрылады.

4. Екі есептің де шешімі бар. Екі есептің де тиімді жоспарларды

бөлшек сандарды қамтиды. Онда осы тиімді жоспарлардағы мақсат функцияларының мәндерін есептейміз. Ең кіші мәні бар мақсат функциясына тиісті есепті қарастырамыз. Осы есептің тиімді жоспарындағы мәні бөлшек болатын компоненттердін бірін таңдаймыз да, осы айнымалының өзгеру облысын оң жағынан және сол жағынан тиісінше бүтін сандармен шектелген екі облысқа бөліп, екі жаңа есепке тармақтаймыз.

Сонымен, жаңа есептен тармақтап тағы жаңа есептер алу үдерісі « 1-есеп» таңбасымен белгіленген төбеден тарамақталған терек түрінде кескіндеуге болады. Бүтін сандық программалау есебінің тиімді шешімін табудағы әрекеттердің осындай тізбегінен әдістің аталуы пайда болды.

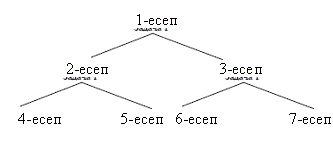
Бастапқы төбе бастапқы 1-есептің тиімді жоспарына сай келеді, ал онымен тармақтар арқылы қосылған төбелер 1-есептің бөлшек санды қамтитын тиімді жоспарындағы бір айнымалы бойынша шектеулер үшін құрылған жаңа есептің тиімді жоспарын білдіреді.

Әрбір төбенің өз тармағы бар. Және бұл кездегі әр қадамда мақсат функциясының мәні кіші болатын тармақ таңдалады.

Егер қайбір қадамда бүтін сандық мәнге иеболатын жоспар алынып,ондағы мақсат функциясының мәні басқа тармақтардағы мақсат функциясының мәнінен кіші немесе соған тең болса онда алынған жоспар бастапқы бүтін сандық программалау есебінің тиімді жоспары болады да, сондағы мақсат функциясының мәні минимум шаманы білдіреді.

Бүтін сандық сызықтық программалау есебін қарастыралық:

(1)

(2)

(3)

­­­ ­- бүтін (4)

Мәселен, әрбір бүтін сандық айнымалының межесінде сөзсіз оның тиімді мәні жататын :

(5)

жоғарғы және төменгі шекараларын көрсете аламыз делік.

Сонымен қатар функционалдық шектеулер жүйесіне (5) теңсіздіктеріндегі р енгізілуі қажет.

Шекаралар мен тармақтар әдісінің кез келген S-ші итерациясында белгілі болуы қажет:

1. Әрқайсысы келесі итерацияларда шешілуі тиіс сызықтық программалау есептерінің негізгі тізімі ( бірінші итерацияда тізім бір есепті қамтиды – (1) есебі және (2-3) пен (5) )

Алғашқы (1)-(3),(5) есебінің сызықтық формасының тиімді мәнінің төменегі шекарасы . Бірінші итерацияда ретінде (2)-(5) облысының ішінде жататын кез келген бүтін сандық нүтесіндегі функциясының мәнін аламыз. Егер мүндай нүктені көрсету қиын болса,онда = , бірақ бұл итерация санын өте көбейтіп жібереді