Вариант 9

(для студентов, номера зачетных книжек которых

оканчиваются цифрой 9)

Задача 1

Имеются следующие данные выборочного обследования деталей 24 машиностроительных заводов:

Номер детали	Длина, м	Номер детали	Длина, М
1	1,56	13	1,55
2	1,39	14	1,63
3	1,54	15	1,49
4	1,56	16	1,43
5	1,50	17	1,37
6	1,58	18	1,53
7	1,59	19	1,58
8	1,52	20	1,43
9	1,40	21	1,60
10	1,44	22	1,47
11	1,62	23	1,43
12	1,62	24	1,53

1) Проведите группировку деталей по длине, образовав 5 групп с равными интервалами. Результаты представьте в виде групповой таблицы.

2) Дайте графическое изображение выборки, постройте гистограмму, полигон, кумуляту.

3) Вычислите выборочные характеристики:

а) выборочное среднее;

б) выборочную дисперсию, выборочное среднее квадратическое отклонение;

в) моду и медиану;

г) коэффициент вариации.

4) С вероятностью 0,95 вычислите предельную ошибку выборочной доли и границы удельного веса деталей длиной не более 1,5 м.

Решение.

Определяем величину интервала

Таблица 1. Статистический ряд распределения

Интервал	1,37-1,422	1,422-1,474	1,474-1,526	1,526-1,578	1,578-1,63	Итого
Количество деталей	3	5	3	6	7	24
Кумулята, S	3	8	11	17	24

Рис. 1 Гистограмма распределения деталей по длине

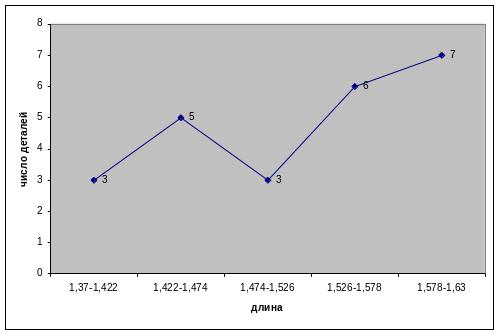
Рис. 2 Полигон распределения деталей по длине

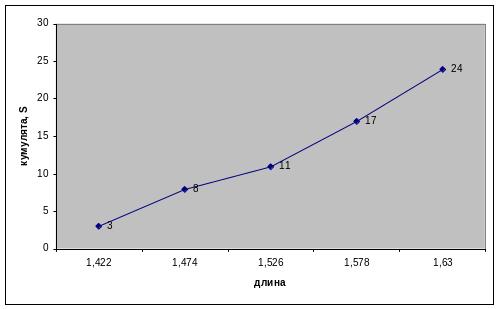
Рис. 3 Кумулята распределения деталей по длине

Таблица 1. Расчет вспомогательных значений для определения характеристик ряда распределения

Интервал	Сере-дина интер-вала, Х	Число автомо-билей, f	Xifi	Куму-лята, S
1,37-1,422	1,396	3	4,188	3	-0,124	0,0461
1,422-1,474	1,448	5	7,24	8	-0,072	0,0259
1,474-1,526	1,5	3	4,5	11	-0,02	0,0012
1,526-1,578	1,552	6	9,312	17	0,032	0,061
1,578-1,63	1,604	7	11,228	24	0,084	0,0494
Итого		24	36,468			0,1288

Выборочное среднее

Выборочная дисперсия

Выборочное среднее квадратическое отклонение

Мода

Большинство деталей имеют среднюю длину 1,58 м

Медиана

Половина деталей имеют длину менее 1,53 м, другая половина – более 1,53 м

Коэффициент вариации

, следовательно, совокупность считается однородной

Предельная ошибка выборочной доли

Границы:

С вероятностью 0,95 доля деталей длиной не более 1,5 м попадает в интервал от 0,22 до 0,62

Задача 2

Имеются данные о количестве выпавших осадков за вегетационный период:

Год	2002	2003	2004	2005	2006	2007	2008	2009
Количество осадков, мм	350	217	140	315	227	212	230	212

1. Вычислить абсолютные и относительные (базисные и цепные) статистические показатели изменения уровней динамики данного ряда.

2. Рассчитать средние показатели динамики ряда.

3. Описать тенденцию ряда с помощью следующих методов сглаживания: а) механического выравнивания по трехлетней скользящей средней; б) аналитического выравнивания по уравнению линейного тренда.

Решение.

Абсолютный прирост

- цепной

- базисный

Темп роста

- цепной

- базисный

Темп прироста

- цепной

- базисный

Абсолютное значение 1% прироста

Таблица 1. Характеристики ряда динамики

Год	Показатель	Абс. прирост		Темп роста		Темп прироста		А1
		Цеп.	Баз.	Цеп.	Баз.	Цеп.	Баз.
2002	350	-	-	100	100	-	-	-
2003	217	-133	-133	62	62	-38	-38	3,5
2004	140	-77	-210	64,5	40	-35,5	-60	2,17
2005	315	175	-35	225	90	125	-10	1,4
2006	227	-88	-123	72,1	64,9	-27,9	-35,1	3,15
2007	212	-15	-138	93,4	60,6	-6,6	-39,4	2,27
2008	230	18	-120	108,5	65,7	8,5	-34,3	2,12
2009	212	-18	-138	92,2	60,6	-7,8	-39,4	2,3

Средний уровень ряда

Средний абсолютный прирост

Средний темп роста

Средний темп прироста

Сглаживание с помощью скользящей средней

Таблица 2. Расчет скользящих средних

t	Y	Трехуровневая сумма	Трехуровневая скользящая средняя
1	350	-	-
2	217	350+217+140=707	235,7
3	140	217+140+315=672	224
4	315	140+315+227=682	227,3
5	227	315+227+212=754	251,3
6	212	227+212+230=669	223
7	230	212+230+212=654	218
8	212	-	-

Аналитическое выравнивание

Уравнение прямой линии:

Для определения параметров используется система уравнений.

Таблица 3. Расчет вспомогательных значений для определения параметров модели

t	Y	Yt	t2	Yp
1	350	350	1	270,08
2	217	434	4	260,88
3	140	420	9	251,68
4	315	1260	16	242,48
5	227	1135	25	233,28
6	212	1272	36	224,08
7	230	1610	49	214,88
8	212	1696	64	205,68
Итого 36	1903	8177	204

Получаем модель

На основании полученных значений можно сделать вывод о среднем снижении показателей