Іv. 3. Основні термодинамічні характеристичні функції. Умови рівноваги

Різний стан однієї і тієї ж термодинамічної системи визначається відмінністю параметрів, що вимірюються і не вимірюються приладами. Функції, через частині похідні яких по відповідних параметрах, виражаються інші термодинамічні параметри стану і термодинамічні властивості системи, називаються характеристичними. Характеристичні функції зручні для аналізу ряду конкретних і таких, що часто зустрічаються на практиці, процесів.

Найбільш широко в термодинаміці використовують такі п’ять характеристичних функцій: 1) внутрішня енергія; 2) ентальпія; 3) ізохорно-ізотермічний потенціал (енергія Гельмгольца); 4) ізобарно-ізотермічний потенціал (енергія Гіббса); 5) ентропія.

Якщо системи складаються з індивідуальних речовин, то кожній із цих функцій можна приписати дві змінні, так би мовити, природні для тієї чи іншої функції. Такі функціональні залежності подаються рівняннями:

U = U(S, V)

H = H(S, p)

A = A(T, V) (ІV.3.1)

G = G(T, p)

S = S(U,V)

Ці залежності означають, що стан простих систем може бути повністю описаний не лише параметрами р, V, Т, але також параметрами U, S, V, або H, S, p, або А, Е, V, або G, Т, р; або S, U,V; причому для системи, що знаходиться в термодинамічній рівновазі, лише два параметри із трьох незалежні. Тому функціональні залежності (ІV.3.1) мають такий же зміст, як і функціональна залежність (І.1.2), тобто є по суті рівнянням стану простих систем.

Вказані в (ІV.3.1) незалежні змінні є характеристичними змінними величин U, H, A, G, S, оскільки вони безпосередньо залежать лише від цих змінних. Величини U, H, A і G можуть бути виражені і через інші (не характеристичні) змінні, наприклад, U = U(V, T), H = H(p, T). Проте такі залежності фактично є опосередкованими через характеристичні, наприклад, U = U(V, T) = U[V, S(V, T)]. Якщо відома яка-небудь із величин U, H, A, G, S, що виражена через свої характеристичні змінні, то через цю величину і її похідні по параметрах стану можуть бути виражені всі решта термодинамічних величин. Тому величини U, H, A, G, S, виражені через свої характеристичні змінні, і називаються характеристичними функціями системи.

Крім термодинамічних характеристичними функціями можуть бути параметри р, Т, V, наприклад, р =  (S,H) тощо. В довільних процесах характеристичні функції прямують до екстремуму (SS_max, GG_min тощо) і досягають його при рівновазі.

Характеристичні функції U, H, A i G іще називають термодинамічними потенціалами.

Із рівняння першого і другого законів термодинаміки

dU = TdS – рdV , (ІV.3.2)

приймаючи почергово сталими або ентропію, або об’єм, можна записати такі частні похідні:

(ІV.3.3)

Таким чином, похідна внутрішньої енергії по ентропії при сталому об’ємі рівна температурі, а похідна по об’єму при сталій ентропії – тиску із знаком мінус. При інших змінних не можна одержати досить простого виразу властивостей системи через похідні від U. Тож для неї об’єм і ентропія – природні змінні, при яких вона характеристична функція. Якщо похідні (ІV.3.3) продиференціювати іще раз, але кожну по іншій змінній, одержуються змішані другі похідні:

, (ІV.3.4)

(ІV.3.5)

Величини змішаних похідних неперервних функцій не залежать від порядку диференціювання і тому такі похідні другого порядку тотожньо рівні між собою. Ця їх властивість доведена в математиці. Тоді на основі (ІV.3.4) і (ІV.3.5) можемо записати таку рівність:

(ІV.3.6)

Як відомо, рівність зберігається, якщо похідні, так би мовити, перевернути. Інакше кажучи, якщо розглядати похідну об’єму по температурі і ентропії по тиску, тобто

(ІV.3.7)

Одержане співвідношення належить до числа так названих рівнянь Максвелла, і назвемо його першим рівнянням.

Для необоротних процесів TdS > dQ, тож

dU < TdS – pdV. (ІV.3.8)

Властивість внутрішньої енергії, як критерію напрямку процесу і стану рівноваги, виявляється, якщо підтримувати сталим об’єм і ентропію. Зменшення внутрішньої енергії в ізохорно-ізоентропійних умовах вказує на самочинний характер процесу, тож

(U)_{S, V} < 0 (ІV.3.9)

Умовою рівноваги є

(U)_{S, V} = 0; (²U)_{S, V} > 0 (ІV.3.10)

Розглянемо тепер ентальпію. За визначенням (ІІ.2.38)

H = U + pV

Якщо продиференціювати це рівняння, одержуємо вираз:

dH = dU + pdV + Vdp (ІV.3.11)

Якщо в цьому виразі замінити dU згідно (ІV.3.2), то матимемо

dH = TdS + Vdp (ІV.3.12)

На підставі рівняння (ІV.3.12) можемо записати дві частині похідні

(ІV.3.13)

, (ІV.3.14)

які показують, що ентальпія є характеристичною функцією при змінних ентропії і тиску. Прирівнювання змішаних похідних другого порядку дає, після відповідного перетворення, друге рівняння Максвелла:

(ІV.3.15)

Для необоротних процесів рівняння (ІV.3.12) запишеться так:

dH < TdS + Vdp (ІV.3.16)

Властивість ентальпії, як критерію напрямку процесу і стану рівноваги, виявляється, якщо підтримувати сталими тиск і ентропію. Зменшення ентальпії в ізобарно-ізоентропійних умовах вказує на самочинний характер процесу, тобто:

(Н)_{р, S} < 0 (ІV.3.17)

Умовою рівноваги є

( Н)_{р, S} = 0 (ІV.3.18)

(²Н)_{р, S} > 0

З рівняння (ІV.2.13) при сталій температурі можна записати

W  T(S₂ – S₁) – (U₂ – U₁)

або

W  (U₁ – TS₁) – (U₂ – TS₂) (ІV.3.19)

Останнє співвідношення показує, що в ізотермічних умовах для оборотних процесів максимальна робота (W_м) може розглядатись як різниця значень функції (U – TS) в початковому і кінцевому стані системи. Нова функція, що виникає, називається ізохорно-ізотермічним потенціалом (скорочено – ізохорним потенціалом) або енергією Гельмгольца. Позначають її символом А і виражається рівнянням:

А = U – TS (ІV.3.20)

Для всякого ізотермічного процесу можна записати:

А = U – TS (ІV.3.21)

або

dА = dU – TdS (ІV.3.22)

Скориставшись рівнянням (ІV.3.19), знаходимо максимальну роботу в ізотермічному процесі, як:

W_м = – А (ІV.3.23)

Зміна ентропії, як було вже зазначено, визначає напрямок і межу самочинних процесів для ізольованих систем. Подібно до цього функція А або енергія Гельмгольца визначає їх для систем, що знаходяться при сталих температурі і об’єму.

Запишемо повний диференціал ізохорного потенціалу, скориставшись рівнянням (ІV.3.20)

dА = dU – TdS – SdТ (ІV.3.24)

Підставимо значення dU із рівняння (ІV.2.14) і одержимо

dА  – SdТ –рdV (ІV.3.25)

Це співвідношення показує, що для ізохорно-ізотермічних процесів, тобто коли dV = 0 і dТ = 0,

(А)_T,V  0 (ІV.3.26)

Отже, в системах, що знаходяться при сталих температурі і об’ємі, самочинно можуть протікати лише ті процеси, які супроводжуються зменшенням А, при цьому межею їх протікання, тобто рівноваги, є досягнення мінімального для даних умов значення функції А, тобто використовується умова

( А)_TV = 0 (ІV.3.27)

(²A)_TV > 0

На підставі рівняння (ІV.3.25) можна також записати дві частні похідні:

(ІV.3.28)

і

(ІV.3.29)

і, продиференціювавши їх іще раз та зробивши відповідні перетворення, одержати третє рівняння Максвелла:

(ІV.3.30)

Якщо розглядати процес при сталій температурі і сталому тиску, то потрібно врахувати і ту енергію, яка витрачається на роботу по розширенню системи, і тоді, замість внутрішньої енергії, користуються ентальпією.

Якщо до правої частини рівняння (ІV.3.20) додати добуток рV, то стане іншим і значення лівої частини. Запишемо сказане у вигляді рівнянь:

G = U – TS + pV (ІV.3.31)

або

G = Н – TS (ІV.3.32)

Для ізотермічного процесу маємо:

G = Н  TS (ІV.3.33)

або

dG = dH – TdS (ІV.3.34)

Введена функція G, як уже відмічалося вище, називається ізобарно-ізотермічним потенціалом (скорочено – ізобарним потенціалом) або енергією Гіббса.

Максимально корисна робота ізобарно-ізотермічного процесу визначається рівнянням

W = – G (ІV.3.35)

Запишемо повний диференціал для ізобарного потенціалу, скориставшись рівнянням (ІV.3.31)

dG = dU – TdS – SdT + pdV + Vdp (ІV.3.36)

Замінивши dU на його значення з рівняння (ІV.2.14), одержуємо

dG  – SdT + Vdp (ІV.3.37)

При dT = 0 i dp = 0

(G)_T,p  0 (ІV.3.38)

В системах, що знаходяться при сталих температурі і тиску, самочинно можуть протікати лише ті процеси, що супроводжуються зменшенням G, при цьому межею їх протікання, тобто умовою рівноваги, служить досягнення деякого мінімального для даних умов значення функції G, тобто виконується умова:

(G)_T,p = 0 (ІV.3.39)

(²G)_T,p > 0

З рівняння (ІV.3.37) витікає, що енергія Гіббса є характеристичною функцією при змінних температурі і тиску. Дійсно

, (ІV.3.40)

(ІV.3.41)

Ці похідні мають в термодинаміці чи не найважливіше значення. Із них уже відомим методом можна одержати четверте рівняння Максвелла:

(ІV.3.42)

Відмітимо, що всі чотири рівняння Максвелла мають дещо спільне: з одного боку, це похідні ентропії по тиску (така похідна негативна) або по об’єму, а з іншого боку, похідні, відповідно або об’єму, або тиску по температурі. Рівняння Максвелла, особливо два останніх, знаходять різноманітне застосування в фізичній хімії.

І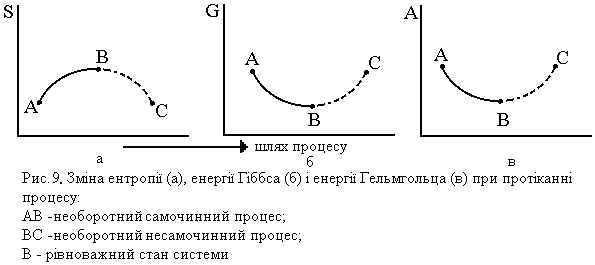 з вище зазначеного слідує, що енергія Гіббса є критерієм напрямку процесу і рівноваги в системі при ізобарно-ізотермічних умовах, а енергія Гельмгольца – критерієм напрямку в ізохорно-ізотермічних умовах.

На рис. 9 подано зміну трьох критеріїв напрямку процесу і стану рівноваги системи (S, G i A). В стані рівноваги системи (точка В) всі три функції досягають екстремального значення: ентропія максимуму, енергія Гіббса і Гельмгольца – мінімуму. Лінії АВ відповідають необоротним процесам, що протікають самочинно, а лінії ВС – не самочинним процесам, для протікання яких системі із зовні потрібно підвести енергію.

Т аким чином, всі характеристичні функції у відповідних умовах слугують критерієм рівноваги або напрямку самочинного процесу. Співвідношення між найважливішими термодинамічними функціями подано на рис. 10.