Лекція 2 Лінійна залежність та незалежність векторів. План.

1.Поняття лінійної залежності та незалежності векторів. Основні теореми.

2. Базис системи векторів.

3. Координати вектора. Дії над векторами в координатній формі.

4. Ортонормовані базиси. Довжина вектора.

5. Приклади розв’язання задач.

1. Нехай задані вектори та числа .

Означення 1. Вектор називається лінійною комбінацією векторів .

У цьому випадку говорять також, що вектор лінійно виражається через вектори .

Означення 2. Якщо рівність

(1) можлива при деяких ненульових коефіцієнтах, то вектори називають лінійно залежними. Якщо ж дана рівність виконується тільки при нульових коефіцієнтах, то вектори називають лінійно незалежними.

Розглянемо деякі твердження, які дають можливість давати відповідь на питання про лінійну залежність чи незалежність векторів без використання означення.

Теорема 1. Вектори лінійно залежні тоді і тільки тоді, коли один із них є лінійною комбінацією інших.

Доведення. Нехай вектори лінійно залежні. Тоді в рівності можна підібрати коефіцієнти так, щоб хоч один із них був відмінний від нуля. Нехай . Тоді , тобто вектор є лінійною комбінацією векторів . Навпаки, якщо один із векторів є лінійною комбінацією інших, наприклад, , то в рівності коефіцієнт біля відмінний від нуля, тому, згідно з означенням, вектори лінійно залежні.

Користуючись даною теоремою, можна стверджувати, наприклад, що вектори , для яких виконується рівність , лінійно залежні. В той же час, якщо два вектори не колінеарні, то вектор напрямлений по діагоналі паралелограма, побудованого на векторах та , буде рівний нулю тільки тоді, коли . У цьому випадку вектори та лінійно незалежні.

Теорема 2. Якщо серед векторів є нульовий вектор, то ці вектори лінійно залежні.

Доведення випливає з рівності (1), в якій достатньо поставити біля нульового вектора відмінний від нуля коефіцієнт, а всі інші коефіцієнти взяти рівними нулю.

Теорема 3. Якщо деяка система векторів містить лінійно залежну підсистему, то ці вектори лінійно залежні.

Для доведення достатньо для підсистеми лінійно залежних векторів виписати рівність (1) з деякими ненульовими коефіцієнтами та доповнити її доданками, одержаними із решти векторів та взятими з нульовими коефіцієнтами.

Теорема 4. Два вектори лінійно залежні тоді і тільки тоді, коли вони колінеарні.

Доведення. Нехай вектори та лінійно залежні та . Оскільки при , а при , то та колінеарні.

Навпаки, нехай дані вектори колінеарні. Розглянемо вектор , де знак «+» вибираємо, якщо і знак «-» - якщо . Очевидно, що . Крім цього, при дістаємо , тобто , а якщо , то , отже, . В обох випадках вектори та співнапрямлені і, оскільки їхні довжини рівні, то . Отже, , або , де . Таким чином, згідно із теоремою 1, вектори та лінійно залежні. Теорема доведена.

Теорема 5. Три вектори лінійно залежні тоді і тільки тоді, коли вони компланарні.

Доведення. Нехай вектори лінійно залежні. Виразимо один із них через інші. Нехай . Позначимо . Точки лежать в одній площині. Цій площині належить також точка , для якої . Отже, вектори компланарні.

Н

Рис. 1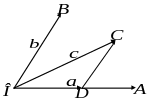

авпаки, нехай вектори компланарні. Вважатимемо, що серед них немає нульових та колінеарних векторів, оскільки в цьому тривіальному випадку вони будуть лінійно залежними (теореми 2 та 3). Від довільної точки відкладемо вектори та проведемо через точку пряму, паралельну до (рис. 1). Нехай дана пряма перетинає пряму в точці . Тоді . Вектори та колінеарні, тому . Аналогічно, , тому . Згідно з теоремою 1 вектори будуть лінійно залежними. Теорема доведена.

Теорема 6. Будь-які чотири геометричні вектори лінійно залежні.

Д

Рис. 2

оведення. Розглянемо чотири вектори . Нехай вектори не компланарні. У випадку компланарності ці три вектори будуть лінійно залежними (теорема 5), тому і всі чотири вектори будуть лінійно залежними (теорема 3). Відкладемо дані вектори від спільної точки . Нехай . Проведемо через точку пряму, паралельну прямій та нехай дана пряма перетне площину в деякій точці. (рис. 2). Тоді . Існують числа та такі, що (теорема 5), (теорема 4). Тому . Згідно з теоремою 1 вектори лінійно залежні. Теорема доведена.

2. Розглянемо деяку множину векторів та її підмножину .

Означення 3. Упорядковану множину векторів називають базисом множини , якщо дані вектори лінійно незалежні, а також будь-який вектор множини лінійно виражається через вектори множини .

Розглянемо в ролі множини множину векторів, які паралельні деякій прямій. Довільний ненульовий вектор цієї множини утворює базис, оскільки будь-який вектор із лінійно виражається через вибраний вектор (теорема 4). Назвемо в цьому випадку множину одновимірним векторним простором колінеарних векторів та позначимо .

Розглянемо множину векторів, які паралельні деякій площині. Базис цієї множини утворюють два довільні неколінеарні вектори. Справді, дані вектори лінійно незалежні (теорема 4), а будь-який третій вектор даної множини через них виражається (теорема 5). Дану множину векторів назвемо двовимірним векторним простором компланарних векторів та позначатимемо дальше .

Якщо в ролі множини взяти множину всіх геометричних векторів, то базис в ній утворять три довільні некомпланарні вектори. Справді, дані вектори лінійно незалежні (теорема 5), а будь-який четвертий вектор через них лінійно виражається (теорема 6). Простір всіх геометричних векторів будемо позначати .

3. Розглянемо простір векторів та довільний його базис . Довільний вектор можна розкласти за цим базисом, тобто подати у вигляді

, (2) причому таке представлення єдине. Справді, припустимо, що розклад вектора можливий із іншими коефіцієнтами, тобто нехай . Віднімаючи від даної рівності рівність (2), дістаємо . Оскільки вектори лінійно незалежні, то одержана рівність можлива тільки при нульових коефіцієнтах. Тому .

Означення 4. Коефіцієнти біля базисних векторів у рівності (1) називають координатами вектора відносно базису .

Координати вектора записують у виді або . Рівність між двома векторами, заданими в координатній формі, будемо розуміти покоординатно, оскільки з рівностей = або випливає, що .

Нехай задані два вектори та . Тоді , тобто

.

Аналогічно доводяться рівності

та

,

де - довільний числовий множник.

У випадку векторного простору та деякого його базису для довільного вектора його координати визначаються, як коефіцієнти біля базисних векторів у рівності . Записують або . Аналогічно, як і у просторі , в просторі додавання та віднімання векторів, а також множення векторів на числа здійснюється виконанням відповідних операцій над координатами.

Теорема 7. Два вектори, задані в координатній формі, колінеарні тоді і тільки тоді, коли їхні координати пропорційні.

Доведення. Нехай задані два колінеарні вектори та . Тоді вони лінійно залежні та існує число таке, що виконується рівність . Вона рівносильна координатним рівностям , , . Якщо , , , то з попередніх рівностей випливає, що , тобто координати пропорційні. Якщо деякі з координат одного з векторів рівні нулю, то відповідні координати у другого колінеарного до нього вектора теж рівні нулю.

Навпаки, якщо виконуються рівності , то, прирівнявши їх до , дістаємо рівність , яка означає колінеарність векторів та .

4. Розглядаючи базис простору , ми накладали на базисні вектори тільки умови упорядкованості та лінійної незалежності. В деяких прикладних задачах обчислення спрощуються, якщо базисні вектори одиничні та взаємно перпендикулярні.

Означення 5. Базис називають прямокутним декартовим (ортонормованим), якщо вектори базису одиничні та взаємно перпендикулярні.

Щоб виділяти ортонормовані базиси використовують спеціальні позначення базисних векторів: . Отже, згідно з означенням, базис - прямокутний декартовий, якщо , . В просторі ортонормованим буде базис .

Нехай в ортонормованому базисі задано вектор та нехай . Відкладемо від деякої точки вектори , , . Очевидно, що вектор співпадає з діагоналлю прямокутного паралелепіпеда, побудованого на векторах , як на сторонах. Оскільки довжини сторін паралелепіпеда рівні , то за відомою властивістю діагоналі прямокутного паралелепіпеда дістаємо або

. (3)

Одержана формула дозволяє обчислювати довжину вектора, знаючи його координати. Відмітимо, що коли одна або дві координати вектора рівні нулю, то при обчисленні його довжини замість довжини діагоналі прямокутного паралелепіпеда доводиться шукати довжину діагоналі прямокутника або довжину вектора, який колінеарний до одного із базисних векторів. В обох випадках дістаємо співвідношення, які є частинним випадком формули (3).

В просторі з вибраним у ньому ортонормованим базисом довжину вектора обчислюють за формулою

.

5. Розглянемо приклади розв’язання задач.

Задача 1. У трикутнику на сторонах і вибрано точки та так, що , а також проведено відрізки і , які перетинаються в точці . У якому відношенні точка ділить дані відрізки?

Розв’язання. Нехай , . Оскільки , то . Виразимо всі вектори в одержаній векторній рівності через та . , . Отже,

.

Оскільки вектори та лінійно незалежні, то, прирівнюючи коефіцієнти біля цих векторів в обох частинах рівності, дістаємо систему рівнянь 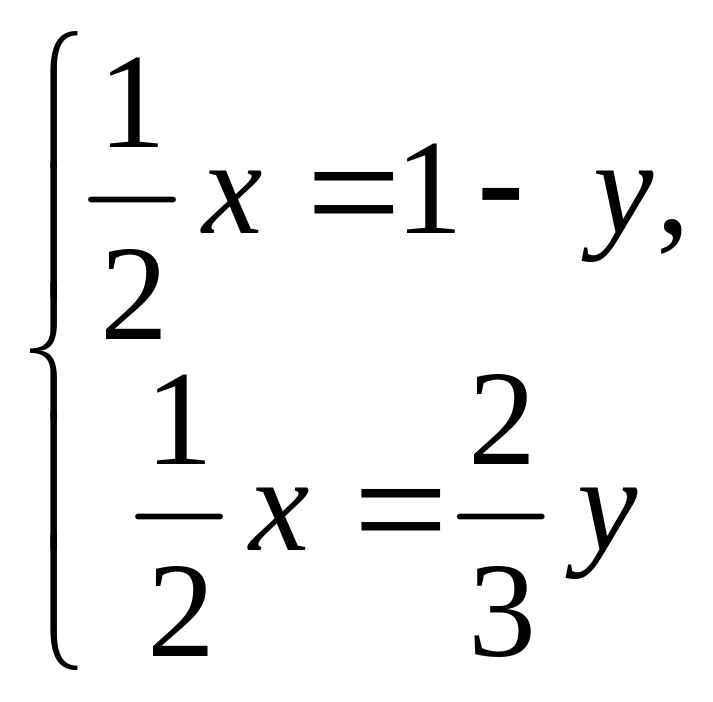, розв’язуючи яку, знаходимо . Отже, .

Відповідь: .

Задача 2. Задано правильний шестикутник . Нехай . Знайти координати векторів та в базисі .

Розв’язання. Нехай - центр кола, описаного навколо заданого шестикутника. Очевидно, що , а також, що . Тому .

Відповідь: .

Задача 3. Довести, що відрізки, які сполучають вершини трикутної піраміди з центрами протилежних граней, перетинаються в одній точці та діляться нею у відношенні 3:1, рахуючи від вершини.

Розв’язання .Нехай - задана піраміда і , точки та - точки перетину медіан трикутників і відповідно, точки належать відрізкам та відповідно, причому . Покажемо, що в базисі координати векторів та співпадають. Маємо

, де - середина відрізка . Отже, в базисі маємо .

Дальше,

, тобто . Таким чином, , тобто точки та співпадають.