138

Рис. 2.49. К определению момента времени , в который происходит возмущение в точке , приходящее в точку в момент времени

Из этого графика видно, что возмущения, происшедшие в точке в другие моменты времени, не придут в точку М в момент времени t, так как график один раз пересекает горизонталь .

Но в точку М в момент времени t придут возмущения из других точек объема , только происшедшие в моменты времени, отличные от . Так, для точки , чтобы возмущение, происшедшее в ней в некоторый момент времени  , пришло в точку М в момент времени t, должно выполняться равенство

. (2.95)

Зарисовав график функции , мы видим, что возмущение, происшедшее в точке в более поздний момент времени по сравнению с , придет в точку М в момент времени t.

Аналогично возмущение из точки , происшедшее в момент времени , придет в точку М в момент времени t. При этом находим из выражения

. (2.96)

Если зарисовать график функции , то можно видеть, что .

Рис. 2.50. Различные положения точечного заряда

Из рис. 2.50 мы видим, что возмущение в точку М в момент времени t придет из всех точек объема , длина которого , а площадь сечения такая же, как и объема . Найдем и .

Из (2.95) и (2.96) следует

. Или

. Или .

Отсюда:

.

Очевидно, для объема можно записать выражение:

. (2.97)

Далее из формулы для запаздывающего скалярного потенциала (2.89):

, где .

Подставляя сюда вместо выражение (2.97), учитывая, что и заменяя обозначение на , и на , получим:

. (2.98)

Чтобы получить выражение для векторного потенциала учтем, что . Тогда исходя из формулы для векторного запаздывающего потенциала (2.93), можно записать

.

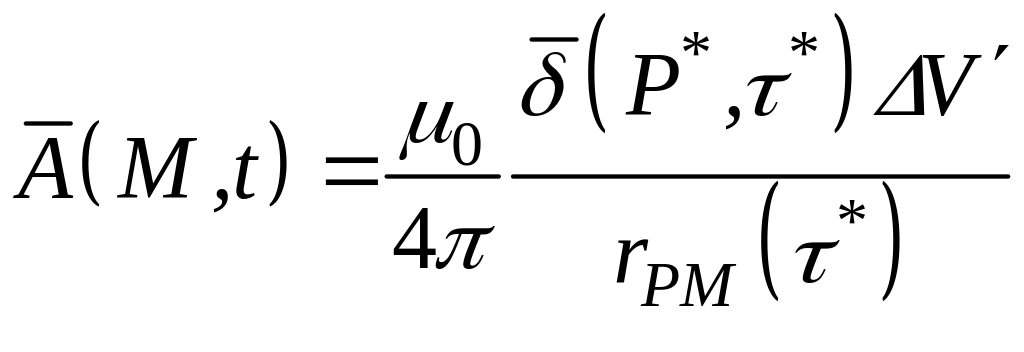Используя выражение (2.97) для и заменяя на , и на , получим:

. (2.99)

Формулы (2.98) и (2.99) являются электродинамическими потенциалами произвольно движущегося точечного заряда. Их называют потенциалами Лиенара-Вихерта.

Между и , как легко видеть, существует связь:

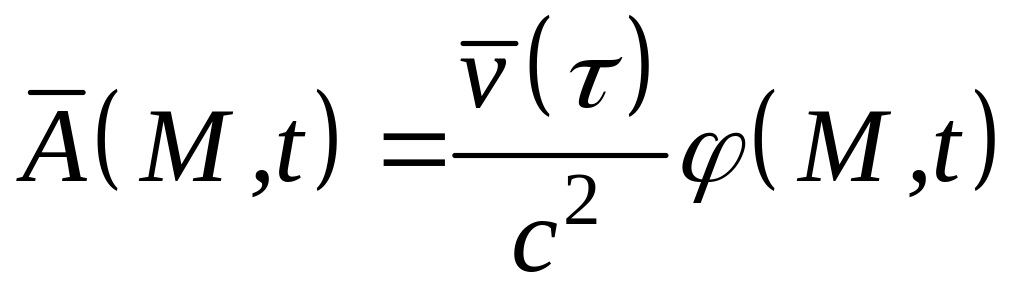. (2.100)

Времена и связаны соотношением:

.

22. Электростатическое поле. Уравнения Пуассона и Лапласа

Электростатическое поле ‑ это электрическое поле неподвижных зарядов. Оно описывается уравнениями:

(2.101)

Или в интегральной форме:

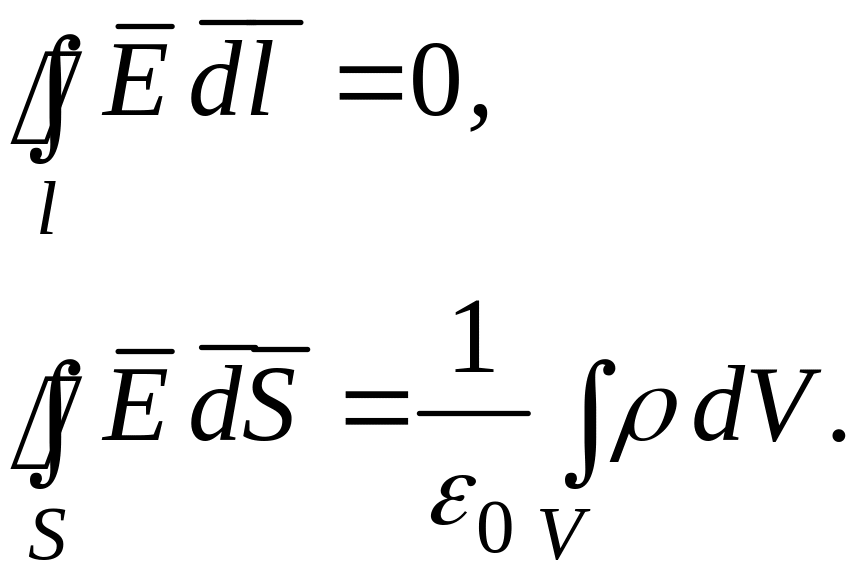(2.102)

Поскольку во всех точках пространства, то можно представить в виде

. (2.103)

Выражение (2.103) является определением электростатического потенциала . Этим выражением потенциал определен с точностью до прибавляемой (аддитивной) постоянной, т.е. если является потенциалом, то , где С ‑ произвольная константа, также является потенциалом, так как

.

Потенциал будет однозначной функцией, если зафиксировать его значение в некоторой точке, например, если положить

. (2.104)

Потенциал, обладающий свойством (2.104), всегда найдется. Действительно, пусть потенциал обладает свойством . Образуем новый потенциал и константу С найдем из условия . Тогда . Отсюда . Т.е. найден потенциал , обладающий свойством (2.104).

Формулы (2.103) и (2.104) являются определением однозначного электростатического потенциала.

Из (2.103) и (2.104) можно получить другое определение электростатического потенциала:

. (2.105)

На самом деле (рис. 2.51):

.

Рис. 2.51. К выводу определения электростатического потенциала в форме интеграла из дифференциальной формы

Здесь использовано выражение (2.103). Далее:

. Здесь – проекция градиента на направление . Далее

. Здесь использовано равенство (2.104). Тем самым получено определение (2.105).

Получим теперь из (2.105) определение (2.103), (2.104). Тем самым будет доказана эквивалентность определений (2.103), (2.104) и (2.105). Из (2.105) (рис. 2.52):

,

.

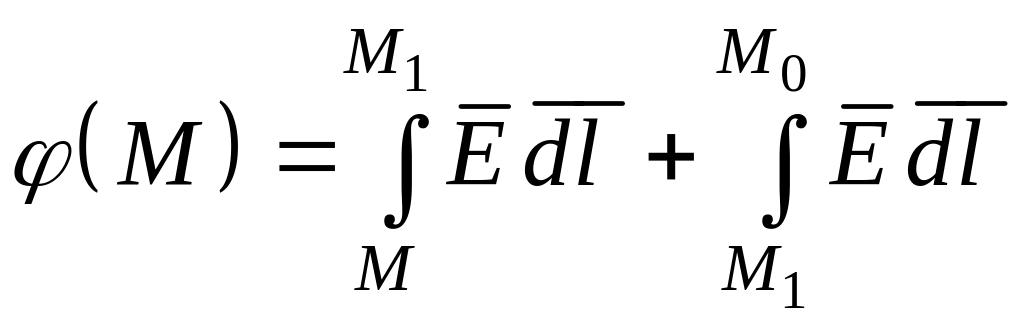Рис. 2.52. К выводу определения электростатического потенциала в дифференциальной форме из интегральной формы

Вычитая из первого равенства второе, получим:

. Или:

.

Отсюда

. Поскольку произвольное направление, то отсюда следует, что , т.е. следует (2.103).

Формула (2.104) непосредственно следует из формулы (2.105), если в ней положить . Эквивалентность определений доказана.

Заметим, что интеграл в (2.105) не зависит от вида пути от точки к точке , а зависит только от положения этих точек. Это легко следует из первого уравнения (2.102).

Если подставить выражение для через потенциал (2.103) в первое уравнение (2.101) ( ), то оно будет удовлетворяться тождественно, а подстановка во второе (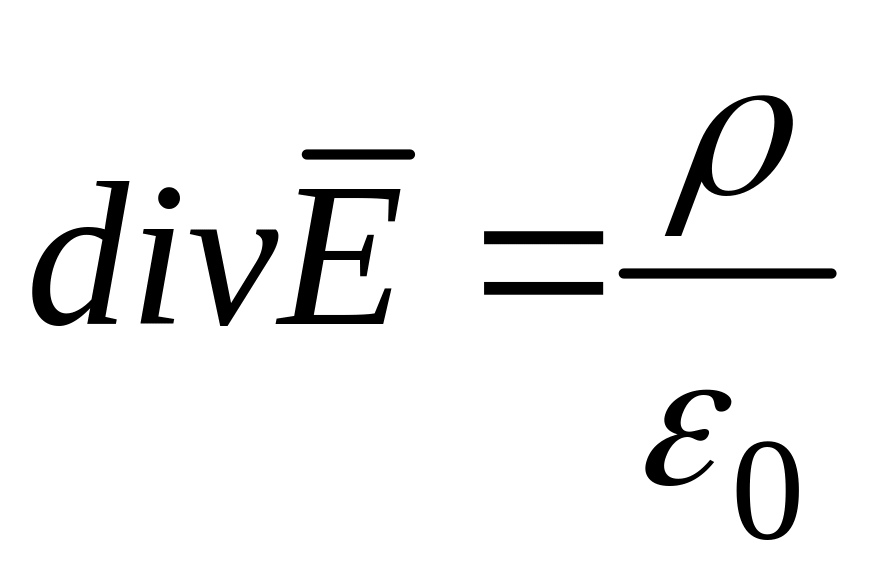 ) дает:

. Если обозначить (лапласиан), то последнее уравнение будет выглядеть так

. (2.106)

Т.е. в общем случае электростатический потенциал удовлетворяет уравнению Пуассона.

В той части пространства, где , электростатический потенциал удовлетворяет уравнению Лапласа:

. (2.107)

23. Потенциал и напряженность электрического поля неподвижных зарядов, находящихся в ограниченном объеме

Пусть заряды распределены в ограниченном объеме V с заданной плотностью . Потенциал в этом случае удовлетворяет следующим уравнениям:

в V,

вне V.

Найдем решение этой системы уравнений косвенным путем. Вначале найдем потенциал точечного заряда q при выборе точки нулевого значения потенциала на бесконечности (рис. 2.53).

Рис. 2.53. К выводу выражения для потенциала точечного заряда

.

Для зарядов, расположенных в объеме V (рис. 2.54) используя данный результат и принцип суперпозиции, находим:

. (2.108)

Рис. 2.54. Объем с заданным распределением плотности заряда

К такому же результату можно прийти, используя скалярный запаздывающий потенциал (2.89), если в нем положить, что не зависит от времени.

Используя выражение для напряженности электрического поля точечного заряда и принцип суперпозиции, получим выражение для напряженности поля зарядов, находящихся в объеме V:

. (2.109)

Эту же формулу можно получить путем взятия градиента со знаком минус от выражения (2.108).

Вопросы и задачи к лекции 9

109-1. Выведите выражение для скалярного потенциала произвольно движущегося точечного заряда. Каким будет это выражение при и при ?

110-2. Выведите выражение для векторного потенциала произвольно движущегося точечного заряда. Каким будет это выражение при и при ?

111-3. Запишите выражение, связывающее векторный и скалярный потенциалы произвольно движущегося точечного заряда.

112-4. Используя формулы для потенциалов Лиенара-Вихерта, найдите скалярный и векторный потенциалы в центре окружности, по которой движется точечный заряд с постоянной угловой скоростью (рис. 2.55). Радиус окружности . В момент времени заряд находился в точке .

Рис. 2.55. К определению потенциалов Лиенара-Вихерта точечного заряда равномерно движущегося по окружности

113-5. Точечный заряд движется равномерно и прямолинейно вдоль оси х (рис. 2.56). Используя потенциалы Лиенара-Вихерта, найдите скалярный и векторный потенциалы в точке в момент времени .

Рис. 2.56. К определению потенциалов Лиенара-Вихерта равномерно движущегося точечного заряда

114-6. Докажите эквивалентность двух определений электростатического потенциала , и .

115-7. Выведите из формулы для запаздывающего скалярного потенциала формулу для электростатического объемного потенциала.

116-8. В объеме V распределены заряды с плотностью . Вне V заряды отсутствуют (рис. 2.57). Запишите дифференциальные уравнения для электростатического потенциала внутри и вне объема V.

Рис. 2.57. К записи дифференциальных уравнений для электростатического потенциала в различных областях

117-9. Используя выражение для напряженности электрического поля точечного заряда и принцип суперпозиции, получите выражение для напряженности электрического поля зарядов, находящихся в объеме V (см задачу 116-8).

118-10. Стержень длиной 2а равномерно заряжен (рис. 2.58). Заряд на единицу длины равен τ. Найдите напряженность электрического поля в точках и . К каким значениям будут стремиться эти напряженности при . В случае найдите напряженности в точках и с помощью теоремы Гаусса в интегральной форме. Сравните эти значения с предельными.

Рис. 2.58. Равномерно заряженный стержень конечной длины

Лекция 10