Задание №1

Решить систему без ЭВМ по методу Прогонки

4x 1	- x 2			=   5
2x 1	+ 3x 2	+ 2x 3		=   2
	- x 2	+ 4x 3	- x 4	=   3
		- x 3	+ x 4	=   5

Определитель матрицы имеет следующий вид:

4 -1 0 0 5 2 3 2 0 2 0 -1 4 -1 3 0 0 -1 1 5

Суть метода состоит в получении в левом нижнем углу нули простыми преобразованиями. Умножим первую строку на -0,5 и прибавим ко второй.

4 -1 0 0 5 0 3.5 2 0 -0.5 0 -1 4 -1 3 0 0 -1 1 5

Умножим вторую строку на 1/3,5 и прибавим ко второй.

4 -1 0 0 5 0 3.5 2 0 -0.5 0 0 4.57 -1 2.86 0 0 -1 1 5

Умножим третью строку на 1/4,57 и прибавим к четвёртой.

4 -1 0 0 5 0 3.5 2 0 -0.5 0 0 4.57 -1 2.86 0 0 0 0.78 5.63

Из четвёртого уравнения можно найти Х_4, из третьего Х_3, из второго Х₂ и из первого Х₁. Подставляя найденную неизвестную в вышестоящее уравнение.

Х₁=0,9

Х₂=-1,4

Х₃=2,2

Х₄=7,2

Проверка:

4*0,9+1,4=5

2*0,9-3*1,4+2*2,2=2

1,4+4*2,2-7,2=3

-2,2+7,2=5

Проверка получилась точная, значит корни уравнения найдены правильно.

Блок схема и алгоритм для метода Прогонки.

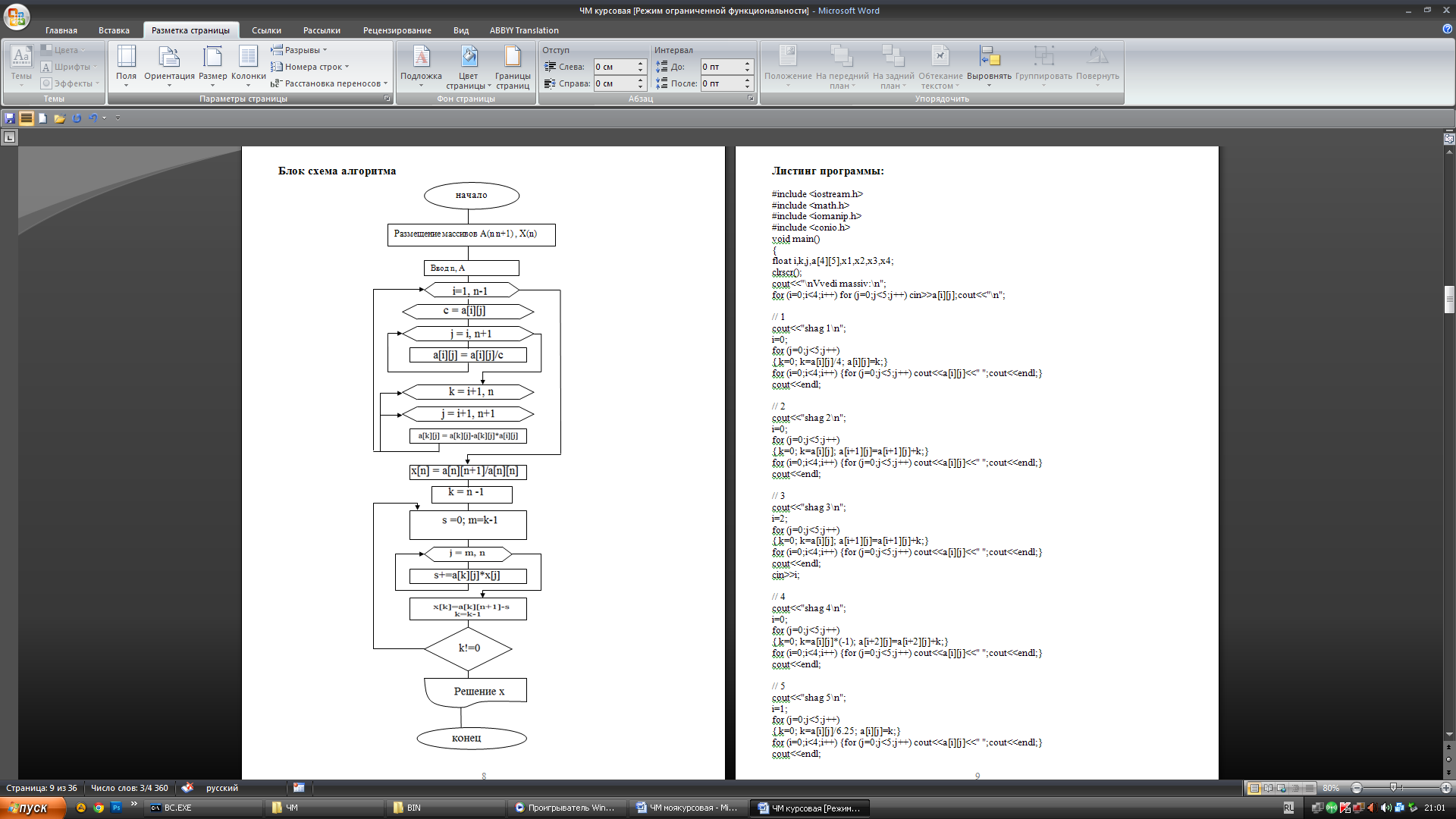
#include <stdio.h>

#include <conio.h>

#include <math.h>

main()

{

clrscr();

float a[50][51], x[50], t;

int i, j, k, m, n;

n=4; m=n+1;

a[0][0]= 4; a[0][1]= -1; a[0][2]=0; a[0][3]=0; a[0][4]=5;

a[1][0]= 2; a[1][1]=3; a[1][2]=2; a[1][3]=0; a[1][4]=2;

a[2][0]= 0; a[2][1]=-1; a[2][2]=4; a[2][3]=-1; a[2][4]=3;

a[3][0]=0; a[3][1]=0; a[3][2]=-1; a[3][3]=1; a[3][4]=5;

printf("matrica \n \n");

for (j = 0; j < n; j++)

{

for (i = 0; i < m; i++)

printf("%6.2f\t", a[j][i]);

printf("\n");

x[j] = 0;

}

for (j = 0; j < n; j++)

if (a[j][i] == 0)

{

k = j;

while ((a[k+1][j] == 0) && (k < n))

k++;

if (a[k+1][j] != 0)

for (i = 0; i < m; i++)

{

t = a[j][i];

a[j][i] = a[k+1][i];

a[k+1][i] = t;

}

else

printf("slau imeet mnogo resheniy");

}

for (k = 0; k < n - 1; k++)

for (j = k + 1; j < n; j++)

{

if (a[k][k] !=0)

{

t = a[j][k] / a[k][k];

for (i = 0; i < n + 1; i++)

a[j][i] = a[k][i] * t - a[j][i];

}

else

printf("slau ne imeet resheniy");

}

printf("\n matrica privedena k treugolnomu vidu:\n\n");

for (j = 0; j < n; j++)

{

for (i = 0; i < n + 1; i++)

printf("%6.2f\t", a[j][i]);

printf("\n");

}

for (j = n - 1 ; j >= 0; j--)

{

t = a[j][n];

for (i = j + 1; i < n; i++)

t= t - a[j][i] * x[i];

x[j] = t / a[j][j];

}

printf("\n korni slay:\n\n");

for (i = 0; i < n; i++)

printf("x%d = %6.2f\n", i, x[i]);

getch();

}

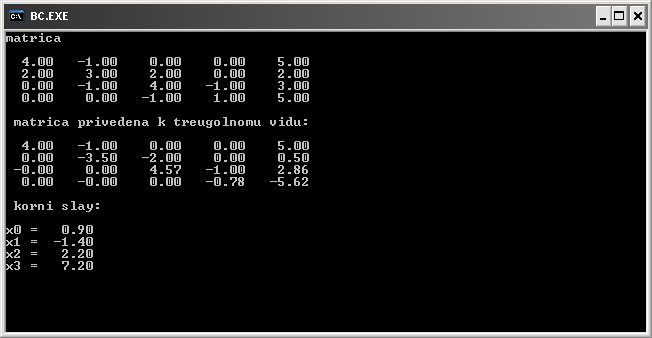
Решение на MATHCAD методом Прогонки.

В в о д и м м а т р и ц у с и с т е м ы и в е к т о р с т о л б е ц с в о б о д н ы х ч л е н о в :

Ф о р м и р у е м р а с ш и р е н н у ю м а т р и ц у :

П р и в о д и м р а с ш и р е н у ю м а т р и ц у к с т у п е н ч а т о м у в и д у :

Ф о р м и р у е м с т о л б е ц р е ш е н и й С Л А У :