13. Особливості вивчення теми«Тригоном. Ф-ції» в класах різного профілю (мета, зміст, методика викладання). Розви-ток пізнавальних інтересів учнів в процесі вивчення теми.

Тема вивч. у 10 кл. Мета+вимоги у прогр. Вивчення триг. ф-й треба будувати на осн. здобутих знань про ф-цію (повтор. осн. шк). Осн. увага приділ. на вивч. ТФ будь-якого числ. аргум. і осн. триг. тотожн. Споч. треба докладн., ніж це було зробл. в 9 кл, розгл. радіанну міру кута (число а що = віднош. довжини дуги до r кола). В радіан. с-мі вимір-ня кутів за 1 береться центр. кут, l=r. Міра цього кута наз. радіаном. Далі треба згадати озн. ТФ кута і поширити їх на будь-яку град. міру, ввести кут повороту. Сказати,що існує відповідність між мн. R чисел і мн. точок од. кола, відп-сті між мн. R чисел і множ. абсцис і ординат т. Р_а од. кола. Ці залежності наз. триг. ф-ціями числ. аргументу.

О. Sin числа a- це ордината т.Р_a; од. кола, в яку переходить поч.т. Р₀ (1 ;0) при повороті навколо центра кола на кут а рад.

О. Cos числа а назв, абсциса точки Р_а од. кола, в яку переходить поч. т. ... (Означ. tg, ctg ч/з відношення Sin і Cos). Викор-чи означ., варто на уроці колект. дослідити хар-р зміни знач. кожної з ТФ і їх знаків. Для tg і ctg використати їх лінії як дотич. Перш ніж вивч. вл. ф-цій доводять їх період., будують графіки. З граф. знаходять ін. властив. а потім обгрунт. їх аналітично. Доцільно виділити 7вл. триг. ф-цій і систематиз. їх так, як буде показано для y=sin x.

1.обл.визн.  R; 2.обл.знач.-[-1,1]. 3. непарна, sin(-x)=-sin х, граф. симетр. віднос. поч. коор. 4. період., найменш. Т= 2. 5. точки перетину з вісями х=0, то у=0 т.б. графік проход. ч/з (0;0); у=0 то х=k, kZ. 6. sinх>0 при х(2n;+2n), sinх<0 х є(+2n; 2+2n); 7. y_max=l в т. /2+2n, a y_min=-l, у т. /2+2n; 8. ф-ція  на (-/2+2n;/2+2n ) і  на (/2+2n; З/2+2n). Графіком є синусоїда. Так само про інші.

У ШКМ є різні підходи щодо введ. arccos, arcsin, arctg, arсctg. Один з них: ці ф-ції ввод. як оберн. ТФ.

Ф-ію f яка має оберн., наз. оборотною. Увага: необх. і дост. ум. існування обер. ф-ції : ф-ія f має набувати кожного свого знач. лише для одного аргументу. Достат. ум. існ-я оберн. ф-ції для даної є її монотон., т.б.  або  на всій обл.визн.

О. Оберненою до даної оборотної (такої, що має обернену) ф-ї у=f(х) наз. ф-я х=(у), яка кожн. у із обл. знач. ф-ї у=f(х) ставить у відповідн. єдине число х з її обл. визн.

Доцільно сформул. уч. алгоритм знаходж. формули ф-ції, оберн, до даної. Дов., що граф. взаємно оберн. ф-цій симетр. відносно у=х. Далі розгл. оберн. ТФ (означення, власт., графіки).

Тригон. р-ня і нерівн. Розв’яз. найпрост. тригон. рівнянь бажано супроводж. зображен. коренів на один. колах і на графіках ф-цій. В 11 кл. слід розгл. найпрост. тригон. р-ня з параметр., напр. cos x=a.Треба домогт., щоб учні зразу могли сказати, що дане рів-ня при ׀а׀>1 не має жодн. розв, при а=1 його задов. всі знач. 2kπ, при а=-1-всі знач. х= π+2kπ, а при ׀а׀<1-всі знач. х=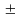 arcos a+2kπ, де k є Z. Треба зауваж., що ТР або зовсім не мають коренів, або безліч, за рахунок періодичності.

Способи розв'яз. триг. рів.: 1)зведення до алгебраїчних (до однієї триг. ф-ї); 2)зведення до однорідних р-нь (cos²x+3sin²x+sin2x=1 - неоднор.) За доп. перетвор.: cos²x+3sin²x+

+2sinxcosx=cos²x+sin²x звести до однорідн.:2sin²x+2sinxcosx=0) 3) розкладання на множн; 4)рівність однойменних ТФ (sin3x=sin5x; 3x+5x=π+2πk) 5) за доп. формул; 6) пониження степеня (cos2x=1-2sin²x) 7) універсальна підстановка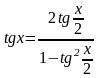 у рівн. виду asinx+bcosx=c; 8) графічний.

З тригон. нерівн. у школі можна обмеж. найпростіш. Нерівності виду sinx<0,5 обов’язк. треба ілюстр. на один. колі або на граф. ф-ції y=sinx. Нерідко учень прав. показ. множину розв. на один. колі, але запис. її у вигляді подв. нерівн. не може. На це треба зверн. особл. увагу.

Обов’язк. слід ознай. учнів з нестанд. завд., які пов’яз. з ТФ.