7.6. Пример вычисления двойного интеграла методом ячеек

Вычислить интеграл

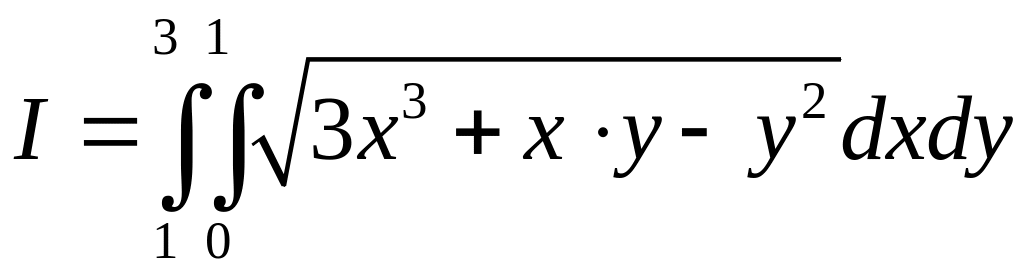. (7.20)

Здесь подъинтегральная функция ; ; ; ; .

Примем количество элементарных отрезков на осях х и у соответственно m = 4, n = 4 (количество узловых точек m + 1 = 5 и n + 1 = 5). Тогда размеры ячеек:

.

Количество ячеек m∙n = 4*4= 16. Расчетная схема представлена на рис. 7.4. Внутри ячеек проставлены их порядковые номера. Координаты узловых точек: x₀ = 1,0; x₁ = 1,5; x₂ = 2,0; … x₄ = 3; y₀ = 0; y₁ = 0,25; … y₄ = 1,0.

Вычисление интеграла (7.20) выполняем непосредственно по формуле (7.18) с учетом того, что размеры всех ячеек одинаковы, т.е. и

Рис. 7.4. Расчетная схема для вычисления интеграла (7.20)

:

7.7. Пример вычисления двойного интеграла методом последовательного вычисления определенных интегралов

Вычислим интеграл (7.20) с использованием формул (7.19). Количество элементарных отрезков и, следовательно, размеры ячеек , и координаты узловых точек такие же, как и в примере, рассматриваемом в п. 7.6.

Для вычисления определенных интегралов, входящих в (7.19), будем использовать формулу трапеций (7.12). Запишем эту формулу применительно к вычислению значения (второе выражение в (7.19)):

. (7.21)

Формулу (7.21) последовательно применяем для вычисления при х = 1,0; 1,5; 2,0; 2,5; 3,0:

; ; .

Здесь вычисления подъинтегральной функции производились по формуле

. Например, при х = 1,5 и у = 0,25

.

Формулу трапеций (7.12) применительно к вычислению двойного интеграла I (первое выражение в (7.19)) запишем следующим образом:

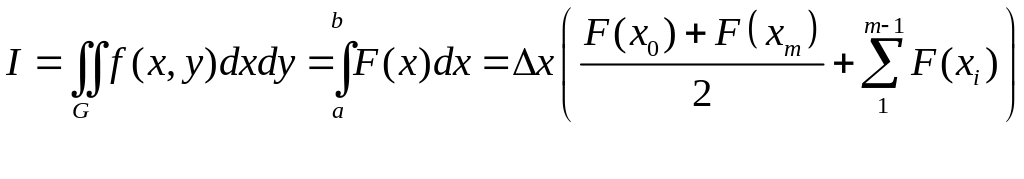(7.22)

Подставляя ранее вычисленные значения в выражение (7.22), получим

.

При вычислении по формуле ячеек этого же интеграла в п. 7.6 ранее получили I = 10,218. Таким образом, относительное отклонение составляет:

.

Отметим, что вычисление двойного интеграла методом последовательного вычисления определенных интегралов по сравнению с методом ячеек требует большего количества вычислений.

65