7.2. Методы прямоугольников и трапеций

Простейшим методом численного интегрирования является метод прямоугольников. Он непосредственно использует замену определенного интеграла интегральной суммой

; (7.5)

. (7.6)

В качестве точек ξ_i выберем средние точки элементарных отрезков [x_i-1, x_i]:

. (7.7)

Тогда (7.5) и (7.6) запишутся так:

; i=1,2,…,n. (7.8)

Формула (7.8) и есть формула прямоугольников. Эта формула использует интерполяцию нулевого порядка (кусочно постоянную) (см. рис. 7.1).

Метод трапеций использует линейную интерполяцию, т.е. график функции у=f(x) представляется в виде ломанной, соединяющей точки с координатами (x_i-1, y_i-1) и (x_i, y_i). В этом случае площадь всей фигуры (криволинейной трапеции) складывается из площадей элементарных прямолинейных трапеций (рис. 7.2).

Площадь каждой элементарной трапеции равна произведению полусуммы оснований на высоту:

; (i= 1,2, … , n) . (7.9)

Складывая площади элементарных фигур, получаем формулу трапеций для численного интегрирования:

. (7.10)

Важным частным случаем рассмотренных формул является их применение при численных интегрирований с постоянным шагом h_i = h = const

Рис. 7.2. Схема к выводу формулы трапеций

( i = 1, 2, …, n). Формулы прямоугольников и трапеций в этом случае принимают соответственно вид:

, (7.11)

(7.12)

7.3. Пример использования методов прямоугольников и трапеций

Вычислить интеграл .

Это табличный интеграл и он вычисляется точно:

Используем теперь формулы прямоугольников и трапеций. Разобьем отрезок интегрирования [0,1] на десять равных частей: n = 10; h = 0,1. Вычислим значения подынтегральной функции в точках разбиения x_i = x_i-1 + h, а также в средних точках (i = 1, 2, …,10). Результаты сведены в табл. 7.1.

Таблица 7.1

Результаты промежуточных вычислений при численном интегрировании

xi	yi
0,0	1,000000
0,1	0,99099	0,05	0,997506
0,2	0,961538	0,15	0,977995
…	…	…	…
0,9	0,552486	0,85	0,580552
1,0	0,500000	0,95	0,525624

Значение интеграла по формуле прямоугольников:

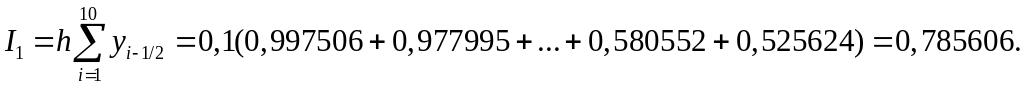
Значение интеграла по формуле трапеций:

Погрешность вычислений по формуле прямоугольников:

.

Погрешность вычислений по формуле трапеций:

Этот пример не очень характерный, так как формула трапеций по сравнению с формулой прямоугольника может дать более точный результат. Это зависит от вида подынтегральной функции.

Уменьшая шаг разбиения можно добиться большей точности численного интегрирования. Правда, увеличить число точек не всегда возможно. Если функция задана в табличном виде (она является результатом экспериментов), то приходится ограничиваться данным множеством точек. Повышение точности в этом случае может быть достигнуто за счет повышения степени используемых интерполяционных многочленов. Использование квадратичной интерполяции приводит к методу Симпсона.