7. Численное интегрирование

7.1. Вводные замечания

Пусть на отрезке [a,b] задана функция y=f(x). С помощью точек x₀,x₁,…,x_n разобьем отрезок [a,b] на n элементарных отрезков [x_i-1, x_i] (i = 1,2,…,n), причем x₀=а, x_n=b. На каждом из этих элементарных отрезков выберем произвольную точку . Найдем произведение S_i значения функции в этой точке f(ξ_i) на длину элементарного отрезка :

. (7.1)

Составим сумму таких произведений

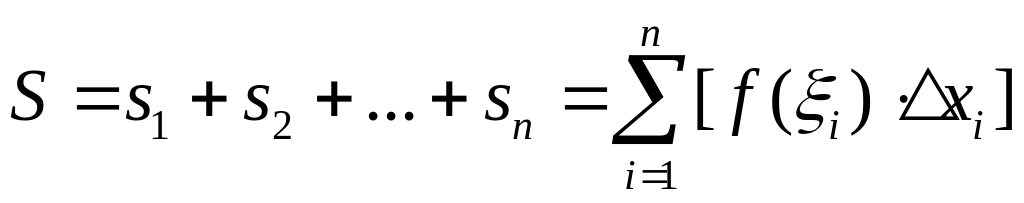. (7.2)

Сумма S называется интегральной суммой. Определенным интегралом от функции f(x) на отрезке [a,b] называется предел интегральной суммы при неограниченном увеличении числа точек разбиения. При этом длина наибольшего из элементарных отрезков стремится к нулю.

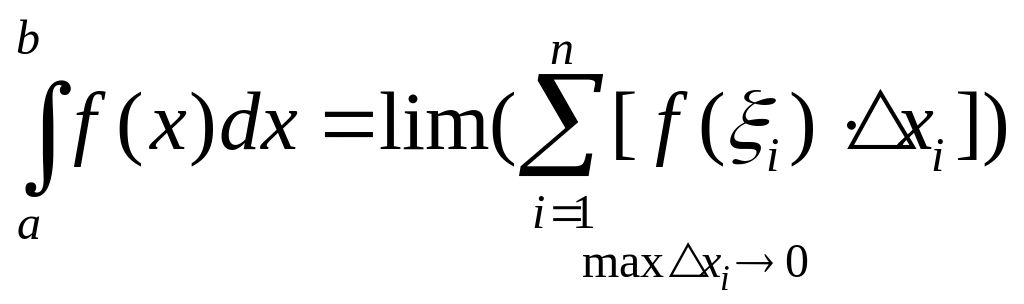. (7.3)

Если функция f(x) непрерывна на отрезке [a,b], то предел интегральной суммы существует и не зависит ни от способа разбиения отрезка [a,b] на

элементарные отрезки, ни от выбора точек ξ_i.

Геометрический смысл введенных понятий для случая проиллюстрирован на рис. 7.1.

Рис. 7.1. Геометрический смысл определенного интеграла

Абсциссами точек М_i являются значения ξ_i, ординатами – значения f(ξ_i). Формула (7.1) при i = 1,2,…,n описывает площади элементарных прямоугольников (штриховые линии). Интегральная сумма (7.2) – площадь ступенчатой фигуры, образуемой этими прямоугольниками. При неограниченном увеличении числа точек деления и стремлении к нулю всех элементов верхняя граница фигуры (ломаная) переходит в линию y=f(x). Площадь полученной фигуры, которую называют криволинейной трапецией, равна определенному интегралу (7.3).

Если подынтегральная функция задана в аналитическом виде,

определенный интеграл равен приращению первообразной F(x) на отрезке интегрирования

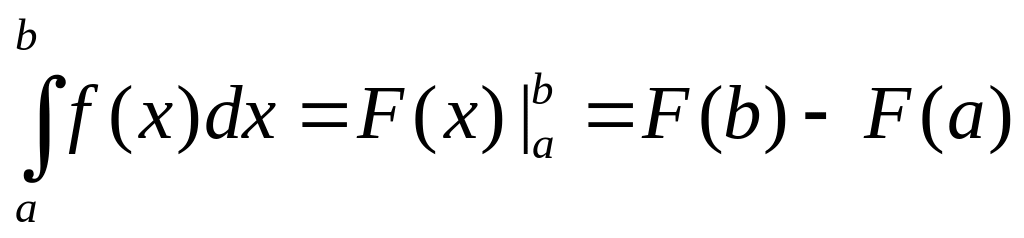. (7.4)

Например, y=f(x)=x²:

.

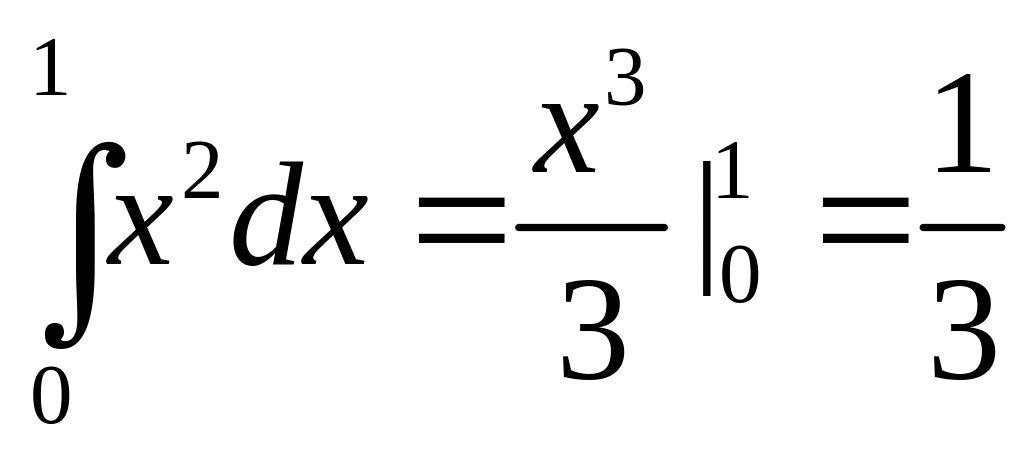На практике формулой (7.4) часто нельзя воспользоваться по двум причинам:

1) вид функции f(x) не допускает непосредственного интегрирования, т.е. первообразную нельзя выразить в элементарных функциях (интеграл не берущийся; он не сводится к стандартному).

2) значения функции f(x) заданы только на фиксированном конечном множестве точек x_i, т.е. функция задана в виде таблицы.

В общих случаях используются методы численного интегрирования. Они основаны на аппроксимации (приближении) подынтегральной функции некоторым более простым выражением, например интерполяционными многочленами.

В дальнейшем будем использовать кусочную (локальную) интерполяцию. Это позволит приближенно заменить определенный интеграл интегральной суммой (7.2). В зависимости от способа вычисления этой суммы получаются разные формулы численного интегрирования: методы прямоугольников, трапеций, парабол и др.

К вычислению определенного интеграла сводятся практические задачи: вычисление площади фигур, определение работы переменной силы и т.д.

55