4.4. Блок – схема итерационного метода Зейделя

Является одним из самых распространенных итерационных методов решения систем линейных уравнений. Блок – схема алгоритма этого метода аналогична другим итерационным методам (см. рис.4.1).

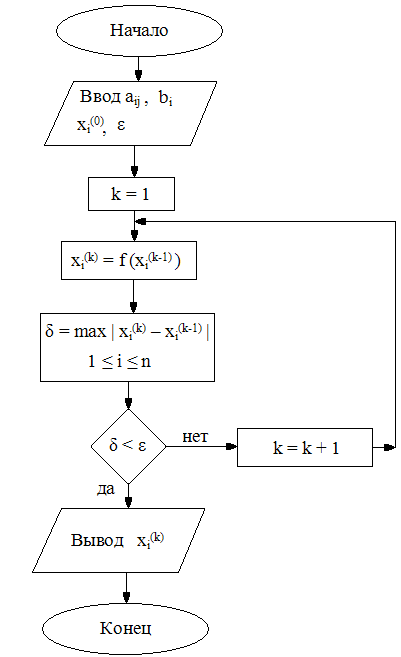
Рис. 4.1. Блок – схема алгоритма итерационного метода Зейделя

Обозначения на рис. 4.1: x_i⁽⁰⁾ – начальные приближения значений неизвестных, k – номер итерации, n – количество уравнений, a_ij – коэффициенты уравнений (при неизвестных x_i), b_i – свободные члены (правые части уравнений), δ – величина, характеризующая близость значений x_i^(k) и x_i^(k-1), ε – точность решения (допустимая величина погрешности).

После выбора начальных приближений организуется циклический вычислительный процесс, каждый цикл которого представляет собой одну итерацию. В результате каждой итерации получаются новые значения неизвестных. При малом изменении этих значений на двух последовательных итерациях вычисления прекращаются. Происходит вывод значений неизвестных, полученных на последней итерации.

4.5. Метод Зейделя

Рассмотрим на примере систем из трех уравнений:

(4.11)

Предположим, что диагональные элементы a₁₁, a₂₂, a₃₃ отличны от нуля. В противном случае нужно переставить уравнения. Выразим неизвестные x₁, x₂, x₃ соответственно из первого, второго и третьего уравнений системы (1):

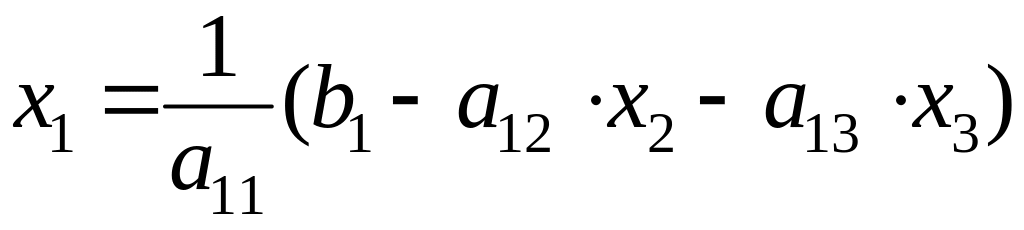, (4.12)

, (4.13)

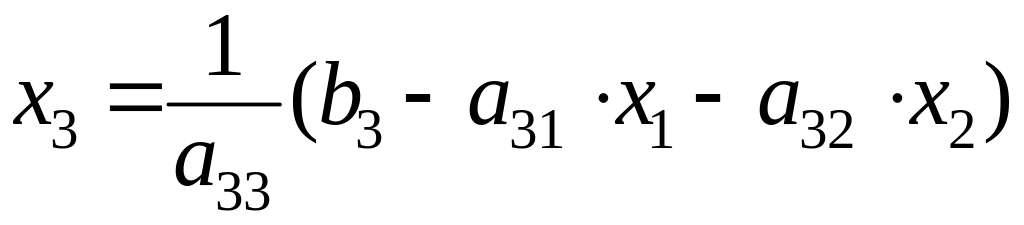. (4.14)

Зададим некоторые начальные (нулевые) приближения значений неизвестных:

.

Подставляя эти значения в правую часть выражения (4.12), получим новое (первое) приближение для x₁:

.

Используя это значение для x₁ (т.е. ) и приближение x₃⁽⁰⁾, находим из (4.13) первое приближение для x₂:

.

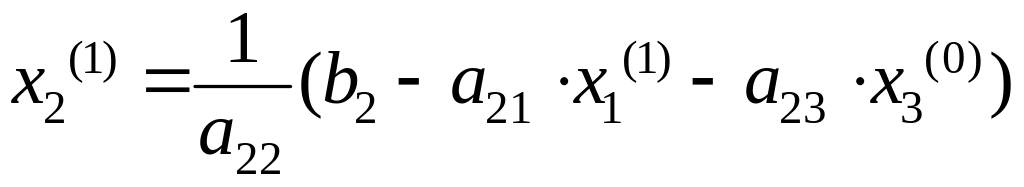И, наконец, используя вычисленные значения x₁ = x₁⁽¹⁾ и x₂ = x₂⁽¹⁾, находим с помощью выражения (4.14) первое приближение для x₃:

.

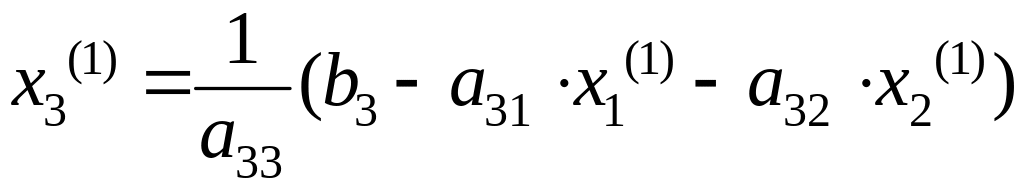На этом заканчивается первая итерация решения системы (4.12), (4.13), (4.14). Используя теперь значения x₁⁽¹⁾, x₂⁽¹⁾, x₃⁽¹⁾, можно таким же способом провести вторую итерацию. В результате нее будут найдены вторые приближения к решению: x₁ = x₁⁽²⁾, x₂ = x₂⁽²⁾, x₃ = x₃⁽²⁾. Затем выполняется третья и последующие итерации. Приближение с номером k можно представить в виде:

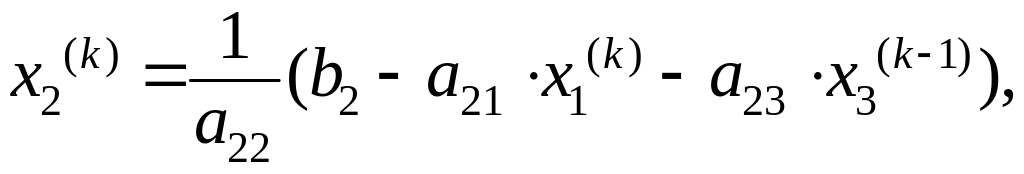
Итерационный процесс продолжается до тех пор, пока значения x₁^(k), x₂^(k), x₃^(k) не станут близкими с заданной погрешностью к значениям x₁^(k-1), x₂^(k-1), x₃^(k-1) . Т.е. вычисляется параметр

.

Если

δ < ε , (4.15)

то процесс прекращается. Величина ε > 0. Это малое, заданное в исходных данных число; ε – погрешность вычисления. Обычно ε = 10^-2…10^-5.

Условия сходимости итерационного процесса рассматривать не будем. Во избежание непроизводительных затрат машинного времени в алгоритм вводят счетчик числа итераций. Если процесс сходится, то вычисления прекращаются при выполнении условия (4.15). Если не сходится, то вычисления прекращаются при достижении числа итераций k некоторого заданного значения M. Число M достаточно большое: M ≥ 500.

Отметим, что для того, чтобы процесс итерационных вычислений сошелся (если он не сходится), можно поменять начальные приближения x_i⁽⁰⁾.