Численные методы
1. Турчак Л.И. Основы численных методов. – М.: Наука, 1987. – 320 с.
2. Демидович Б.В. Основы вычислительной математики. – М.: Наука, 1970.–664 с.
3. Шуп Т. Прикладные численные методы в физике и технике. – М.: Высшая школа, 1990. – 225 с.
4. Дьяконов В.П. Справочник по алгоритмам и программам на языке БЕЙСИК для ПЭВМ. – М.: Наука, 1987. – 240 с.
1. Этапы решения задачи на пк
1. Постановка задачи. Производится содержательная (физическая) постановка задачи и определяются конечные цели решения.
2. Построение математической модели (математическая формулировка задачи). Модель должна правильно (адекватно) описывать основные законы физического процесса. Построение математической модели требует глубокого понимания проблемы и знания соответствующих разделов математики.
3. Разработка или выбор численного метода. ПК выполняет только простейшие операции. Поэтому он «не понимает» постановки задачи даже в математической формулировке. Для решения задачи должен быть найден численный метод, позволяющий свести задачу к вычислительному алгоритму. Разработкой численных методов занимаются специалисты в области вычислительной математики. Специалисту-прикладнику необходимо для решения задачи из широкого арсенала методов выбрать тот, который наиболее подходит в данном конкретном случае.
4. Разработка алгоритма и построение блок-схемы. Алгоритм решения – последовательность элементарных арифметических или логических операций, приводящих к конечному результату. Алгоритм можно изобразить в виде блок-схемы.
5. Программирование. Алгоритм решения задачи записывается на
понятном машине языке в виде точно определенной последовательности операций. В результате получаем программу для ПК. Программирование проводится на алгоритмических языках: Паскаль, БЕЙСИК, BASIC-Visual, Q-Basic, С++, Delphi (современная версия Паскаля), Фортран. Трансляция или компиляция – это перевод с алгоритмического языка на язык ПК. Это выполняется автоматически самой вычислительной системой. Есть так называемые машинно-ориентированные языки – Ассемблер.
Можно использовать пакеты прикладных программ, в которых реализованы практически все численные методы - Maple, Mathсad, Matlab и др.
6. Отладка программы. Программа испытывается на решении контрольных (тестовых) задач для проверки достоверности результатов.
7. Проведение расчетов. Готовятся исходные данные и производится расчет по отлаженной программе.
8. Анализ результатов.
2. Методы решения математических задач
Для решения математических задач используются следующие основные группы методов: 1) графические, 2) аналитические, 3) численные.
1.
Графические методы
в ряде случаев позволяют оценить порядок
искомой величины. Решение находится
путем геометрических построений.
Например, для нахождения корней уравнения
строится график функции
,
точки пересечения которого с осью
абсцисс и будут искомыми корнями (рис.
2.1).
;
.
2. Аналитические методы. При их использовании решение задачи удается выразить с помощью формул. Аналитически решаются простейшие алгебраические или трансцендентные уравнения; вычисляются табличные интегралы; решаются дифференциальные уравнения. В этом случае
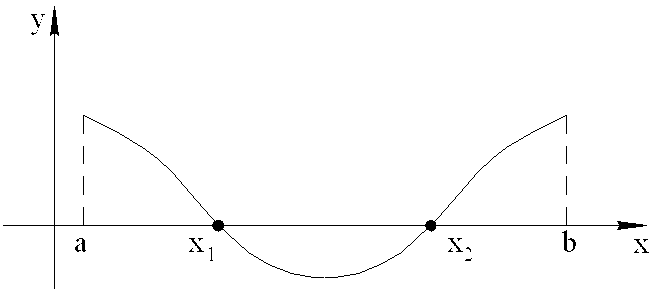
Рис. 2.1. Графическое определение корней уравнения на заданном отрезке [a, b]
используются известные из математики приемы и формулы. Например,
;
;
.
На практике свести решение задачи только к использованию аналитических методов удается редко.
3. Численные методы. Основной инструмент для решения сложных математических задач. Они позволяют свести решение задачи к выполнению конечного числа простых арифметических и логических действий над числами. Результаты получаются в виде числовых значений.
Аналитически:
.
Численно:
- конкретное число.
Многие численные методы разработаны давно. Однако при вычислении вручную они могли использоваться лишь для решения не слишком трудоемких задач. С появлением ЭВМ началось бурное внедрение численных методов в практику.
Численный метод должен обладать 2 свойствами:
а) необходимо получать результат за приемлемое время;
б) он не должен вносить в вычислительный процесс значительных
погрешностей.