11. Пропускная способность канала без помех.

Для теории и практики важно выяснить, до какого предела и каким путем можно повысить скорость передачи информации по конкретному каналу связи. Предельные возможности канала по передаче информации характеризуются его пропускной способностью.

Пропускная способность канала С_д равна той максимальной скорости передачи информации по данному каналу, которой можно достигнуть при самых совершенных способах передачи и приема:

При заданном алфавите символов и фиксированных основных характеристиках канала (например, полосе частот, средней и пиковой мощности передатчика) остальные характеристики должны быть выбраны такими, чтобы обеспечить наибольшую скорость передачи по нему элементарных сигналов, т. е. обеспечить максимальное значение V_Т. Максимум среднего количества информации, приходящейся на один символ принятого сигнала I(V,U), определяется на множестве распределений вероятностей между символами u₁...u_i...u_m.

Пропускная способность канала, как и скорость передачи информации по каналу, измеряется числом двоичных единиц информации в секунду (дв. ед./с).

Так как в отсутствие помех имеет место взаимно-однозначное соответствие между множеством символов {ν} на выходе канала и {u} на его входе, то I(V,U) = =I(U,V) = H(U). Максимум возможного количества информации на символ равен log m, где m — объем алфавита символов, откуда пропускная способность дискретного канала без помех

C_Д=V_T*log_m

Следовательно, для увеличения скорости передачи информации по дискретному каналу без помех и приближения ее к пропускной способности канала последовательность букв сообщения должна подвергнуться такому преобразованию в кодере, при котором различные символы в его выходной последовательности появлялись бы по возможности равновероятно, а статистические связи между ними отсутствовали бы. Доказано, что это выполнимо для любой эргодической последовательности букв, если кодирование осуществлять блоками такой длины, при которой справедлива теорема об их асимптотической равновероятности.

Расширение объема алфавита символов m приводит к повышению пропускной способности канала, однако возрастает и сложность технической реализации.

12. Исправление одиночных или обнаружение двойных ошибок.

Прежде чем исправить одиночную ошибку в принятой комбинации из n разрядов, необходимо определить, какой из разрядов был искажен. Это можно сделать только в том случае, если каждой одиночной ошибке в определенном разряде соответствуют свой класс вычетов и свой опознаватель. Так как в циклическом коде опознавателями ошибок являются остатки от деления многочленов ошибок на образующий многочлен кода g(x), то g(x) должно обеспечить требуемое число различных остатков при делении векторов ошибок с единицей в искаженном разряде. Как отмечалось, наибольшее число остатков дает неприводимый многочлен. При степени многочлена m = n - k он может дать 2^n-k-1 ненулевых остатков (нулевой остаток является опознавателем безошибочной передачи).

Следовательно, необходимым условием исправления любой одиночной ошибки является выполнение неравенства

где С_n — общее число разновидностей одиночных ошибок в кодовой комбинации из n символов; отсюда находим степень образующего многочлена кода

и общее число символов в кодовой комбинации. Наибольшие значения k и n для различных m можно найти, пользуясь табл. 6.11.

Как указывалось, образующий многочлен g(x) должен быть делителем двучлена хⁿ⁺¹. Доказано, что любой двучлен типа может быть представлен произведением всех неприводимых многочленов, степени которых являются делителями числа m (от 1 до m включительно). Следовательно, для любого m существует по крайней мере один неприводимый многочлен степени m, входящий сомножителем в разложение двучлена хⁿ⁺¹.

Таблица 6.11

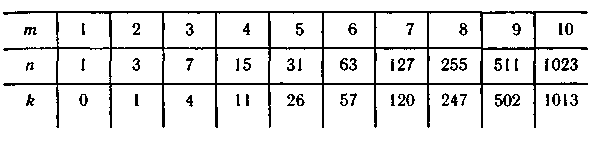
Пользуясь этим свойством, а также таблицами многочленов, неприводимых при двоичных коэффициентах, выбрать образующий многочлен при известных n и m несложно. Определив образующий многочлен, необходимо убедиться в том, что он обеспечивает заданное число остатков.

В табл. 6.12 приведены основные характеристики некоторых кодов, способных исправлять одиночные ошибки или обнаруживать все одиночные и двойные ошибки.

Таблица 6.12

Это циклические коды Хэмминга для исправления одной ошибки, в которых в отличие от групповых кодов Хэмминга все проверочные разряды размещаются в конце кодовой комбинации.

Эти коды могут быть использованы для обнаружения любых двойных ошибок. Многочлен, соответствующий вектору двойной ошибки, имеет вид ξ(χ) = xⁱ + xⁱ, или ξ(x) = xⁱ(x^j-i + 1) при j>i. Так как j-i<n а g(x) не кратен x и принадлежит показателю степени n, то ξ(x) не делится на g(x), что и позволяет обнаружить двойные ошибки.