3. Сообщение как случайный процесс
Информация поступает в систему в форме сообщений. Под сообщением понимают совокупность знаков или первичных сигналов, содержащих информацию. Источник сообщений в общем случае образует совокупность источника информации ИИ (исследуемого или наблюдаемого объекта) и первичного преобразователя ПП (датчика, человека-оператора и т.п.), воспринимающего информацию о его состояниях или протекающем в нем процессе. Различают дискретные и непрерывные сообщения.
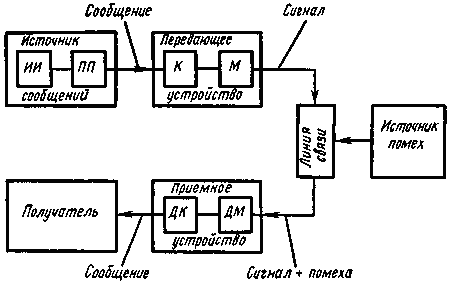
рис: Структурная схема одноканальной системы передачи информации
Дискретные сообщения формируются в результате последовательной выдачи источником отдельных элементов — знаков. Множество различных знаков называют алфавитом источника сообщений, а число знаков — объемом алфавита. В частности, знаками могут быть буквы естественного или искусственного языка, удовлетворяющие определенным правилам взаимосвязи. Распространенной разновидностью дискретных сообщений являются данные.
Непрерывные сообщения не разделимы на элементы. Они описываются функциями времени, принимающими непрерывное множество значений. Типичными примерами непрерывных сообщений могут служить речь, телевизионное изображение. В ряде систем связи непрерывные сообщения с целью повышения качества передачи преобразуются в дискретные.
Для передачи сообщения по каналу связи ему необходимо поставить в соответствие определенный сигнал. В информационных системах под сигналом понимают физический процесс, отображающий (несущий) сообщение. Преобразование сообщения в сигнал, удобный для передачи по данному каналу связи, называют кодированием в широком смысле слова. Операцию восстановления сообщения по принятому сигналу называют декодированием.
Так как число возможных дискретных сообщений при неограниченном увеличении времени стремится к бесконечности, а за достаточно большой промежуток времени весьма велико, то ясно, что создать для каждого сообщения свой сигнал практически невозможно. Однако, поскольку дискретные сообщения складываются из знаков, имеется возможность обойтись конечным числом образцовых сигналов, соответствующих отдельным знакам алфавита источника.
4. Сигналы ам и чм в виде временного, спектрального и векторного вида.
Модуляцией называют нелинейное явление, при котором несколько сигналов взаимодействуют друг с другом таким образом, что в результате получается сигнал с новыми частотами, отсутствовавшими в исходных.
Модулируемая частота называется несущей. На представленном спектре максимальная по амплитуде компонента и есть несущая, а другие составляющие, которые похожи на гармоники, называют боковыми полосами. Последние располагаются симметрично по обеим сторонам от несущей с шагом, равным величине модулирующей частоты Частотная модуляция часто встречается в спектрах вибрации машин, особенно в зубчатых передачах, где частота зацепления зубьев модулируется оборотной частотой колеса. Она также имеет место в некоторых акустических динамиках, хотя и на очень низком уровне.
Для анализа модулированных колебаний будем пользоваться тремя различными представлениями о сигнале: временным, спектральным (частотным) и векторным.
Временный вид: по оси абсцисс отложено время t, а по оси ординат — мгновенное значение амплитуды U. Спектральный вид: по оси абсцисс отложена частота f=w/2pi, по оси ординат — амплитуда. Синусоидальное колебание изображается в виде отрезка прямой линии, параллельной оси ординат. Длина отрезка соответствует амплитуде колебания U, а его положение на оси абсцисс— частоте fo. Векторный вид: синусоидальное колебание представлено в виде вектора, вращающегося против часовой стрелки с угловой скоростью wo=2pi*f0=2pi/T0, где Т0 — период колебания. Длина вектора соответствует амплитуде U, а угол f0 — начальной фазе, при которой начат отсчет времени.
а-временная диаграмма модулирующего сигнала;
б-временная диаграмма амплитудно-модулированного сигнала;
в, г, д, е - спектральные (частотные) и векторные диаграммы.
При частотной и фазовой модуляции длина вектора U остается постоянной. Изменяется во времени его положение на плоскости. Вектор как бы качается относительно первоначального положения. Угол отклонения dф называется девиацией фазы. Отклонение частоты df от своего номинального значения fo называется девиацией частоты.
Разница между частотной и фазовой модуляцией заключается в том, что при фазовой модуляции мгновенное изменение фазового угла происходит по закону изменения низкочастотного сигнала, а при частотной модуляции по такому закону изменяется мгновенная частота. Определить, является ли данный сигнал частотномодулированным или фазо-модулированным, можно только в том случае, если известен закон изменения низкочастотного сигнала. Между обоими видами модуляции существует вполне определенная математическая зависимость. В обоих случаях вектор, соответствующий модулированному сигналу, вращается вокруг своего начала не равномерно, а с некоторой переменной угловой скоростью.