Задача № 2

Строительным управлением принят к строительству объект нулевого цикла, который включает: 1) погрузку свай на складе, 2) транспортировку свай, 3) разгрузку, 4) погружение свай, 5) срезку оголовков свай.

На балансе организации имеются следующие машины, которые по своим техническим параметрам могут выполнить технологический цикл. Удельные приведенные затраты на выполнение единицы объема работ (р./шт.) указаны на стрелках возможных связей машин (рис. 4)

Требуется выбрать по одной марке машин в комплект с наименьшими удельными приведенными затратами.

Рис. 4

Задача № 3

Строительное управление имеет на балансе четыре экскаватора различной размерной группы, три вида самосвалов, два вида автогрейдеров и катков. Все эти машины при анализе их технических возможностей могут выполнять технологический процесс строительства автодороги.

Необходимо сформировать комплект машин, состоящий из одного экскаватора, самосвала одной марки, автогрейдера и катка для строительства автодороги суммарными удельными приведенными затратами (рис.5). Приведенные затраты на выполнение единицы объема работ (руб./м³) указаны на стрелках возможных связей машин (рис.5).

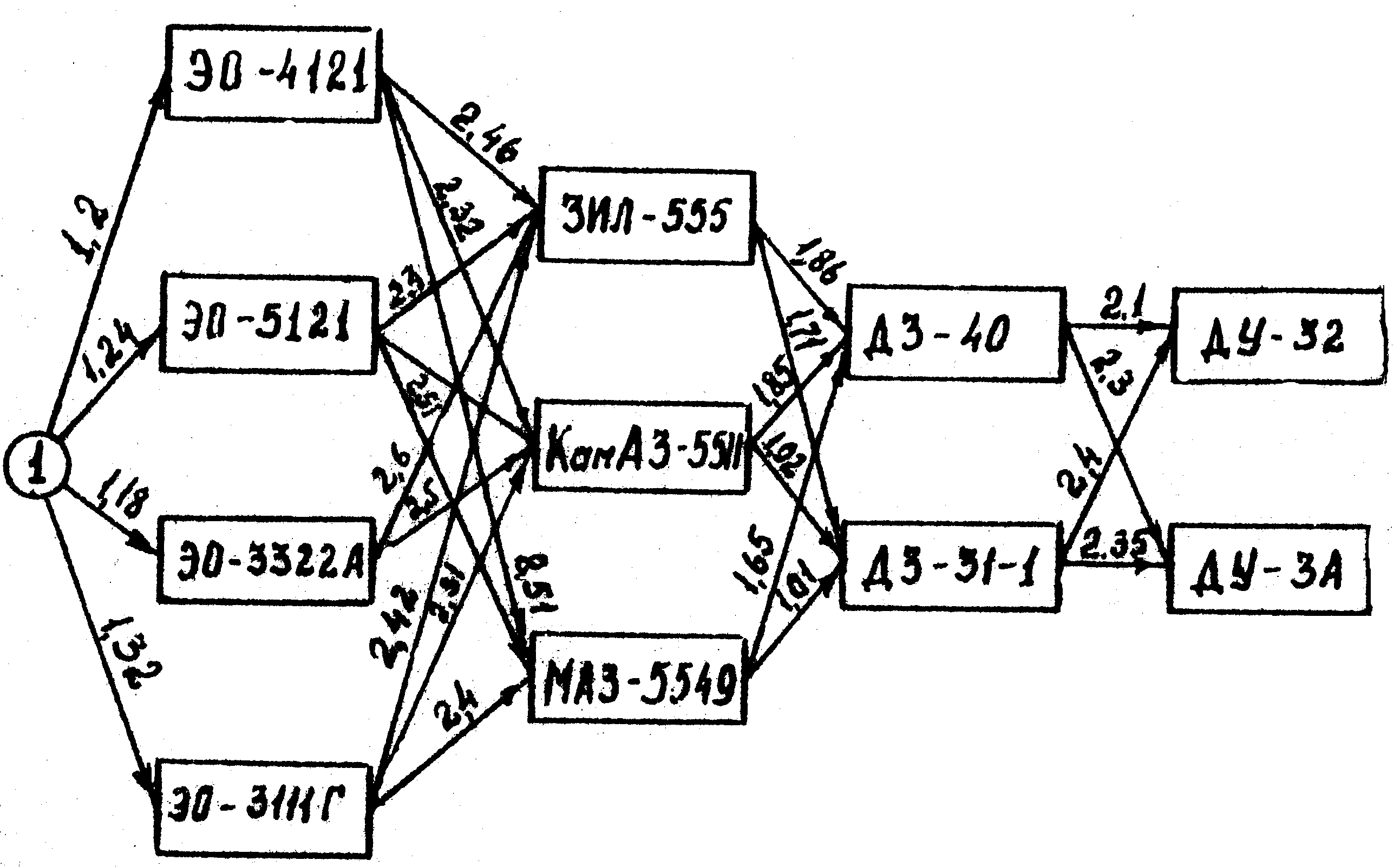
Рис. 5

3 Распределение комплектов машин по объектам строительства

При распределении машин по объектам строительства перед инженерно-техническими работниками может возникнуть несколько задач, которые имеют рациональные решения. Часто встречающейся задачей может быть распределение количества машин, равного количеству строящихся объектов по различным критериям (минимальные суммарные затраты или минимальное время на строительство всех объектов в течение года). Для решения данной задачи наиболее приемлем венгерский метод.

1. Пример: В строительной организации имеются пять башенных кранов КБ-307А -2 шт.; КБ-306 - 2 шт.; и КБ - 401Б. В планируемом году принято к строительству 5 объектов. Время на монтаж каждого объекта соответствующим краном подсчитано при разработке проекта производства работ. Необходимо расставить краны по объектам строительства так, чтобы суммарное время производства работ было минимальным. Исходные данные представлены в табл. 1.

Таблица 1

Марка кранов	Затраты времени на монтаж Сij по объектам Bj, ч
	В1	В2	В3	В4	В5
1. КБ – 307А	80	70	90	100	60
2. КБ – 308	50	40	30	60	70
3. КБ – 401Б	30	40	50	60	70
4. КБ – 307А	80	70	90	100	60
5. КБ – 308	50	40	30	60	70

Решение: Критерий оптимизации: суммарное время монтажа 5-и объектов математически можно записать так:

,

Задача решается при условии ограничения:

1. Каждый кран работает на одном объекте;

2. На каждом объекте может работать 1 кран, т.е.

,

.

Алгоритм метода включает следующие этапы:

1) Получение нулей в каждой строке. Для этого в строке выбирается наименьшее значение времени и записывается в столбец di табл.2.

Таблица 2

Марка машины	Затраты времени на монтаж Сij по объектам Вj, ч					di
	В1	В2	В3	В4	В5
A1	80	70	90	100	60	60
А2	50	40	30	60	70	30
А3	30	40	50	60	70	30
А4	80	70	90	100	60	60
A5	50	40	30	60	70	30

di - минимальный элемент строки вычисляется из всех элементов и получаем новую матрицу, табл. 3.

Таблица 3

Марка машины	Затраты времени на монтаж Сij по объектам Bj, ч.					di
	В1	В2	В3	В4	В5
A1	20	10	30	40	0	-
А2	20	10	0	30	40	-
А3	0	10	20	30	40	-
А4	20	10	30	40	0	-
A5	20	I0	0	30	40	-
di	0	10	0	30	0	-

Аналогично выполняется операция для столбцов Bj и получаем результаты представленные в табл. 4.

Таблица 4

Марка машины	Машины	Затраты времени на монтаж С ij по объектам Вj, ч.
		В1	В2	В3	В4	В5
A1	КБ - 307А	20	0*	30	10	0X
А2	КБ - 308	20	0X	0*	0X	40
А3	КБ - 401Б	0*	0X	20	0X	40
А4	КБ - 307А	20	0X	30	10	0*
A5	КБ - 308	20	0X	0X	0*	40

В каждой строке и столбце есть 0 (нули).

2) Поиск оптимального решения. Рассматриваем одну из строк табл. 4 с наименьшим количеством нулей и отмечаем нуль звездочкой *, а остальные нули зачеркиваем в строке и столбце. Аналогично для всех строк. Получили пять звездочек по одной в каждой строке. Решение оптимально!

На 1-м объекте работать должен кран А₃ КБ – 401Б; на 2-м A₁ КБ - 307А;

на 3-м A₂ КБ - 308; на 4-м А₅ КБ - 308; на 5-м A₄ КБ - 307А.

Суммарное время на монтаж объектов:

ΣY= 70 + 30 + 30 + 60 + 60 = 250 ч.

Задача № 4

Таблица 5

Марки машины	Затраты на выполнение работ Cij по объектам Bj тыс. р.
	В1	В2	В3	В4	В5	В6	В7
1	120	112	116	125	122	118	121
2	126	118	131	116	134	121	125
3	124	131	118	121	119	125	118
4	132	119	123	126	118	131	116
5	118	124	119	127	124	128	119
6	116	117	124	119	130	120	131
7	125	116	125	117	120	132	120

Задача № 5. Таблица 6

Марка машин	Затраты времени на монтаж Сij по объектам Bj, дни
	В1	B2	В3	В4	В5	В6	В7	В8
1	81	69	76	72	80	75	70	71
2	80	73	75	71	79	80	76	73
3	71	76	70	80	69	82	78	70
4	83	74	76	70	81	69	73	78
5	70	69	82	76	78	71	69	80
6	81	83	77	74	76	75	69	81
7	72	70	74	75	80	81	70	73
8	80	73	73	80	79	76	73	72

Задача № 6. Таблица 7

Марки машин	Затраты на выполнение работ, Cij по объектам Вj, р.
	В1	В2	В3	В4	В5	В6
1	234	246	240	238	241	245
2	230	238	235	241	243	237
3	243	240	234	238	240	234
4	236	244	241	244	245	238
5	240	243	238	237	234	240
6	238	241	240	238	244	234

Задача № 7 Таблица 8

Марки машин	Затраты времени на монтаж Cij по объектам Вj, ч.
	В1	В2	В3	В4	В5	В6	В7	В8	В9
1	24	28	31	36	25	29	30	34	32
2	28	31	36	24	29	25	34	32	30
3	36	29	30	28	27	30	28	24	27
4	24	28	31	36	25	29	30	34	32
5	34	28	34	30	26	32	29	28	34
6	26	23	28	29	34	36	25	28	24
7	28	31	36	24	29	25	34	32	30
8	36	29	30	28	27	30	28	24	27
9	28	30	36	27	24	21	32	25	26

2. При выборе объемов работ на планируемый период строительная организация имеет определенную технику. Исходя из годовой выработки каждой машины, инженерно-техническая служба будет ограничиваться суммарным объемом работ по объектам, равным суммарной годовой выработке машин. При этом количество объектов может быть не равным количеству машин, имеющихся в парке. Данные задачи не имеют на сегодняшний день окончательного решения одним методом.

Поэтому такие типы задач решаются шестью способами одновременно. Затем берут наиболее удачное решение с min затратами и проверяют полученное решение на оптимальность. Для решения данных задач пользуются исходными данными удельных приведенных затрат на выполнение единицы продукции либо по статистическим данным организации, либо по расчетным значениям проекта производства работ (ППР).

Пример: В строительной организации имеются 6 бульдозеров, у которых суммарная годовая выработка составила в прошлом году 132 тыс.м³ разработанного грунта. При этом известны приведенные затраты Сij, связанные с выполнением единицы работы каждой машиной. Формируя объемы работ на следующий год, строительная организация выбрала 4 объекта с общим объемом земляных работ 132 тыс.м³. Требуется расставить бульдозеры по строящимся объектам так, чтобы суммарные затраты были минимальны. Исходные данные приведены в табл. 9. Таблица 9

Марка бульдозера	Затраты на выполнение единицы работы Сij по объектам Вj, р./м3				Годовая выработка машин Пi тыс. м3
	В1	В2	В3	В4
ДЗ-422 (А1)	20	38	51	16	18
ДЗ-42Г (А2)	32	18	48	71	14
ДЗ-42Г-1 (А3)	19	36	18	44	20
ДЗ-110В (А4)	18	24	55	67	26
ДЗ-116В (А5)	69	28	36	18	31
ДЗ-117А (А6)	41	56	24	32	23
Годовой объем работ, Vj тыс.м3	19	33	46	34	132

Решение задачи возможно при основной закономерности:

Критерий оптимизации - суммарные затраты на выполнение всех работ - можно записать: