Лекция 9. Ситуации равновесия в игре

ОПР. Пара стратегий игроков является ситуацией равновесия игры, если для любой другой пары стратегий имеет место неравенство:

Ситуация равновесия характерна тем, что ни один игрок не имеет разумных оснований для изменения своей стратегии, при условии, что другой игрок придерживается своей равновесной стратегии.

Например, игры с платежными матрицами

			1
			1
	1	0	3

			0
			1
	0	2	4

обладают двумя равновесными ситуациями в чистых стратегиях . Отступление одного из игроков от любой из этих равновесных ситуаций, при условии, что второй игрок ее придерживается, приводит к проигрышу отступившего игрока.

Не всякая игра имеет ситуацию равновесия в чистых стратегиях.

Например, игра в орлянку такой ситуации не имеет:

Если игра обладает ситуацией равновесия , то говорят, что игра разрешима. В этом случае решением игры называется указание одной из (или всех) равновесных ситуаций игры и определение выигрышей и игроков в равновесной ситуации игры.

Замечание: игры рассмотренного выше типа называются играми с ненулевой суммой или биматричными играми.

Особенностью таких игр является тот факт, что ситуация равновесия не является абсолютно устойчивой и возможно возникновение математически не формализуемых ситуаций (переговоров, шантажа, угроз и т.п.)

Пример 1. «Семейный спор»

Рассмотрим биматричную игру.

Молодая семья: муж I игрок, жена II. Выбирают одно из двух развлечений на вечер: матч бокса или балет. Муж предпочитает балет, жена бокс. Однако обоим предпочтительнее быть вместе.

Очевидно, чистые стратегии и образуют ситуацию равновесия, причем ситуации и не являются равновесными, однако выигрыши в ситуации равновесия различны.

Ситуация предпочтительна для игрока один, а - для игрока два. Даже если игрок один знает, что игрок два выберет чистую стратегию , он может настаивать на использовании , а не , надеясь, что это заставит игрока два переключиться на .

Даже в случае, когда имеется только одна ситуация равновесия, может возникнуть неустойчивость.

Пример 2. «Дилемма заключенного»

Рассмотрим игру. Два преступника в разных КПЗ подозреваются в тяжком преступлении. Однако прямых улик нет, и обвинения в значительной мере зависят от того, сознаются ли они сами.

Если сознаются, то на большой срок, но не самый большой.

Если ни один из них не сознается, то обвинение в тяжком преступлении снимается, но суд может доказать их виновность (небольшое наказание).

Если один лишь сознается, а второй будет хранить молчание, то первый будет выпущен на свободу, а второй получит максимальный срок.

Игра имеет единственную ситуацию равновесия . Она определяет вектор выигрышей (1,1), но если оба игрока сыграют «неправильно», т.е. выберут свои первые чистые стратегии, то в результате получится выигрыш (5,5), что лучше для обоих. Но каждый игроков может выиграть еще больше, предав другого.

Поэтому в играх с ненулевой суммой говорят только о ситуации равновесии, а не об оптимальных стратегиях.

Рассмотрим два примера, на которых проиллюстрируем основные идеи решения дискретных позиционных игр с полной информацией.

Игру ведут два игрока, обладающих полной информацией о состоянии игры. Каждой позиции игры с личным ходом игрока имеются только две альтернативы. В позиции игры со случайным ходом также имеется только две альтернативы с вероятностным распределением .

Требуется определить ожидаемые выигрыши игроков и их равновесные стратегии. Запись реализации игры на графе принята в виде двоичного числа:

0 – левая альтернатива;

1 – правая.

Пример 1. Решить игру без случайных ходов при четырех личных ходах:

первый ход – первого игрока;

второй ход – второго игрока;

третий ход – первого игрока;

четвертый ход – второго игрока.

Выигрыши игроков в зависимости от партии игры представлены в таблице:

Партия
0000	-6,48	-5,25
0001	9,81	-3,05
0010	4,54	-7,52
0011	3,14	-2,06
0100	5,65	5,43
0101	-5,59	-8,95
0110	6,64	-9,5
0111	0,5	6,18
1000	4,71	7,45
1001	-3,98	0,98
1010	3,27	-1,23
1011	6,74	-0,52
1100	1,11	-9,92
1101	7,22	-1,04
1110	-1,15	-3,53
1111	-2,63	7,17

Сформулируем ход рассуждений первого и второго игрока:

второй игрок: «Я нахожусь в позиции перед последним ходом. Выбор оптимального ребра альтернативы определяется наибольшим выигрышем:

первый игрок: «Я нахожусь в позиции ,j=1,2,3,4, мой выигрыш зависит от решения противника в позициях . Буду ориентироваться на выбор противником оптимального хода, и выбирая ребро-альтернативу, приводящее к наибольшему выигрышу. Если я отступлю от этой стратегии, в то время как противник будет придерживаться своей оптимальной стратегии, то я могу только потерять. Выбираю стратегию:

Повторяя рассуждения, приходим к начальной вершине А.

Итак, стратегия первого игрока:

а второго:

Если любой игрок отступает от выбранной стратегии, при условии, что второй игрок ее придерживается, то он может только потерять. Т.О., эти стратегии образуют ситуацию равновесия в игре.

. Пример 2.

Решить игру из трех ходов.

первый ход – первого игрока;

второй ход – случайный;

третий ход – второго игрока

Вероятностное распределение для случайного хода и

Выигрыш игроков в зависимости от партии игры представлен в таблице.

Партия
000	9,78	-8,88
001	4,86	-1,39
010	7,46	6,39
011	4,01	5,26
100	-7,33	-5,57
101	-7,06	1,34
110	6,38	6,95
111	8,89	7,42

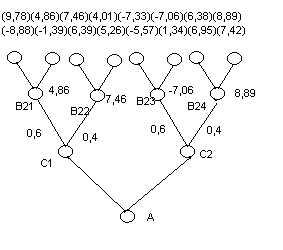
Строим рассуждения второго игрока в позициях из множества вершин и определяем оптимальные ходы в этих позициях.

Первый игрок, ориентируясь по оптимальному поведению второго игрока, может сосчитать матем ожидание своего выигрыша при выборе хода в позиции А.

Левая альтернатива

Правая альтернатива

Т.О. равновесные стратегии игроков имеют вид:

Основная теорема: Любая конечная дискретная позиционная игра двух игроков с полной информацией имеет ситуацию равновесия в чистых стратегиях.