Комментарии к Главе 2

{2К1}

ВОЛЬТМЕТР (voltmeter) - электроизмерительный прибор для измерения электрического напряжения. По способу представления результата измерения В. разделяются на аналоговые и цифровые.

У аналоговых для получения результата производится отсчёт показания по положению указателя на шкале, а у цифровых результат непосредственно представлен в виде именованного числа, выражающего результат измерения. Аналоговые В. по элементной базе разделяются на электромеханические и электронные. Основу электромеханических составляют различные измерительные механизмы – магнитоэлектрический, электромагнитный, электродинамический, ферродинамический, электростатический, а основу электронных – усилители и выпрямители (с магнитоэлектрическим механизмом на выходе).

Основными характеристиками любого В. являются: род измеряемого напряжения (постоянное, переменное), диапазон измерения, класс точности, входное сопротивление, частотный диапазон (для В., измеряющих переменное напряжение). По роду измеряемого напряжения В. разделяются на измеряющие только напряжение постоянного тока, только напряжение переменного тока и универсальные, т.е. способные измерять и то и другое.

Показания В., измеряющих переменное напряжение, обычно соответствуют действующему значению этого напряжения. При этом некоторые В. по своему принципу действия реагируют именно на действующее значение, независимо от формы кривой напряжения, если только его спектр не выходит за пределы частотного диапазона В. (например, электромагнитные). Многие В. реагируют на другие значения, например, на средневыпрямленное (выпрямительные В.), но результат представляют в действующих значениях для синусоидальной формы кривой напряжения. Такие В. в принципе дают правильный результат только при измерении синусоидального напряжения.

Особую группу составляют импульсные В., показание которых соответствуют максимальному значению импульса.

Чем больше входное сопротивление В., тем меньше погрешность от взаимодействия В. с источником измеряемого напряжения. Это объясняется тем, что при измерении напряжения между какими-либо двумя точками электрической цепи экспериментатора обычно интересует значение этого напряжения до подключения вольтметра. Подключение В. в большей или меньшей степени – в зависимости от соотношения между его входным сопротивлением и выходным сопротивлением источника измеряемого напряжения – уменьшает это напряжение, т.е. создаёт погрешность.

Входное сопротивление электромеханических В. составляет килоомы, электронных – мегаомы, цифровых – до гигаомов. У электромеханических В. обычно нормируется не входное сопротивление, а ток полного отклонения указателя “на всю шкалу”, который для многопредельных В. с переключаемыми добавочными резисторами остаётся одним и тем же на разных пределах.

Для В., измеряющих переменное напряжение в широком диапазоне частот, существенно не только активное входное сопротивление, но и входная ёмкость, составляющая обычно единицы пикофарад. В этом случае говорят не о входном сопротивлении, а о входном импедансе. Входной импеданс В. – это параллельное соединение входного сопротивления и входной ёмкости. Верхняя граница частотного диапазона достигает у электромагнитных, электро- и ферродинамических В. единиц килогерц, у выпрямительных – десятков килогерц, у электростатических, термоэлектрических – мегагерц, у некоторых электронных аналоговых и цифровых – гигагерц.

{2К2}

АМПЕРМЕТР (ammeter) - прибор для измерения электрического тока.

Основу электромеханических аналоговых А., т.е. приборов со шкалой и указателем, образуют измерительные механизмы. Для измерения постоянного тока используются магнитоэлектрические приборы (микроамперметры, миллиамперметры, амперметры и килоамперметры). При значении верхнего предела диапазона измерения 20 – 30 мА ничего кроме собственно измерительного механизма не требуется, для измерения бoльших токов (А, кА) применяют шунты. Для измерения очень малых значений постоянного тока (верхний предел 1 мкА и менее) служат гальванометры. Переносные А. имеют классы точности 0,1; 0,2 и 0,5. Обычно они имеют много (до нескольких десятков) переключаемых пределов измерения. Щитовые магнитоэлектрические А. обычно однопредельные и имеют классы точности 1,0 и 1,5.

Электромагнитные, электродинамические и ферродинамические А. предназначены для измерения действующего значения переменного тока, причём их показания не зависят от формы кривой тока, если его спектр не выходит за пределы частотного диапазона прибора. Они могут измерять и постоянный ток, причём показания электродинамических А. принципиально одинаковы на постоянном и переменном токе, если значение постоянного тока равно действующему значению переменного тока. Это позволяет обеспечивать высшие классы точности 0,1 и 0,2 у этих А., потому что их можно точно проградуировать на постоянном токе, а применять на переменном. Показания электромагнитных и ферродинамических А. немного различаются на постоянном и переменном токе из-за потерь энергии в магнитопроводе на перемагничивание и на вихревые токи. Классы точности этих А. обычно не выше 0,5. Обеспечение нескольких (чаще двух, обычно не более четырёх) пределов измерения у электромагнитных А. достигается секционированием обмотки, у электродинамических и ферродинамических – переключением соединения подвижной и неподвижной обмоток с последовательного (для токов до 0,5 А) на параллельное.

Расширение пределов измерения в сторону больших токов достигается применением трансформаторов тока. Верхняя граница частотного диапазона А. переменного тока не превышает нескольких килогерц. Более широкий частотный диапазон достигается у А. на основе магнитоэлектрических измерительных механизмов с преобразователями переменного тока в постоянный: до нескольких десятков килогерц у выпрямительных А. (с преобразователями на полупроводниковых диодах) и до нескольких мегагерц у термоэлектрических А. (с преобразователями на термопаре с нагревателем, по которому протекает измеряемый ток). Классы точности этих А. обычно не выше 1,0; диапазон измерения выпрямительных А. – от единиц миллиампер до единиц ампер, термоэлектрических – от десятых долей миллиампера до 100 А. Чаще всего выпрямительные А. выпускают универсальными, т.е. способными измерять как переменный, так и постоянный ток (отключение преобразователя) и комбинированными, т.е. предназначенными для измерения не только токов, но и напряжений, а иногда и сопротивлений. Универсальные А. имеют разные шкалы для постоянного и переменного тока. В отличие от других приборов, выпрямительные предназначены для переменного тока только синусоидальной формы.

Цифровые А. не выпускаются, но измерение тока (постоянного и переменного) входит в число функций, выполняемых комбинированными приборами (мультиметрами), в основе которых лежит цифровой вольтметр с входными преобразователями различных измеряемых величин в постоянное напряжение.

{2К3}

ИЗМЕРИТЕЛЬНЫЙ МЕХАНИЗМ (measuring mechanism) – совокупность элементов средства измерений, которые обеспечивают необходимое перемещение указателя (стрелки, светового пятна и т. д.). Термин относится к электромеханическим измерительным приборам. Существует шесть типов измерительных механизмов: магнитоэлектрический, электромагнитный, электродинамический, ферродинамический, электростатический и индукционный. В основе каждого из них лежат фундаментальные законы электричества. Например, магнитоэлектрический И.м. основан на силовом действии магнитного поля на проводник с током.

Во всех измерительных механизмах электрическая энергия, создаваемая измеряемой величиной (ток, напряжение и др.), преобразуется в механическую энергию углового перемещения подвижной части. При этом возникает вращающий момент, поворачивающий подвижную часть в сторону возрастающих показаний. Если бы этому повороту ничего не препятствовало, то подвижная часть при любом значении измеряемой величины, отличном от нуля, повернулась бы до упора (это относится ко всем И.м., кроме индукционного). Но при повороте подвижной части образуется ещё и противодействующий момент, направленный навстречу вращающему и пропорциональный углу поворота. Он создаётся упругими элементами, – растяжками, на которых подвешена подвижная часть, или спиральными пружинками, если подвижная часть крепится на оси, – которые закручиваются при повороте. По достижении равенства вращающего и противодействующего моментов подвижная часть останавливается и по положению указателя на шкале можно делать отсчёт значения измеряемой величины.

{2К4}

ИЗМЕРИТЕЛЬНЫЙ МЕХАНИЗМ МАГНИТОЭЛЕКТРИЧЕСКИЙ (moving-coil measuring mechanism) – измерительный механизм, в котором вращающий момент возникает в результате взаимодействия магнитного поля постоянного магнита и магнитного поля катушки с измеряемым током. Используют И.м.м. с подвижной катушкой или с подвижным магнитом. И.м.м. с подвижной катушкой применяются в электромеханических амперметрах, вольтметрах, гальванометрах, омметрах, а с подвижным магнитом – в вибрационных гальванометрах.

Одна из конструкций И.м.м. представлена на рис. 1. Магнитную цепь И.м.м. образуют постоянный магнит 1 и изготовленные из магнитомягкого материала полюсные наконечники 3, сердечник 4 и магнитопровод 5. В воздушном зазоре между сердечником и полюсными наконечниками, где создается равномерное радиальное магнитное поле, помещается подвижная катушка 2 прямоугольной формы, подвешенная на растяжках 8. С подвижной катушкой скреплена стрелка 7, уравновешенная грузиками 6. Цепь измеряемого тока состоит из обмотки катушки и последовательно соединенных с ней растяжек, которые создают противодействующий момент M_пр, пропорциональный углу  отклонения катушки: M_пр = W, где W = const – удельный противодействующий момент.

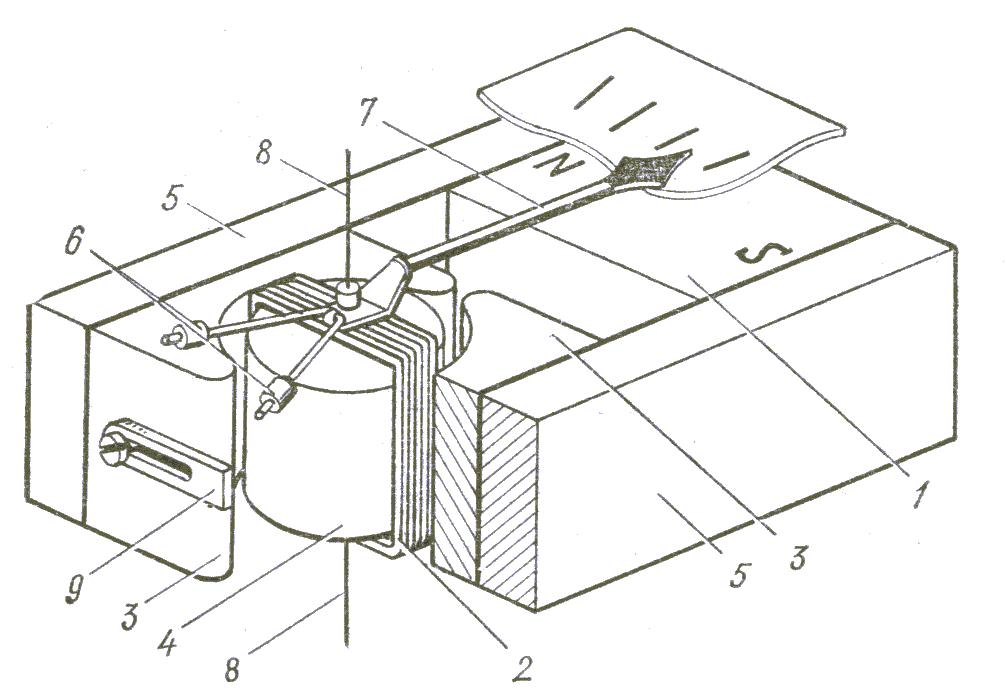
Рис. 1. Магнитоэлектрический измерительный механизм.

При постоянном токе I возникает вращающий момент M = BswI, где B – магнитная индукция в воздушном зазоре, s – площадь катушки, w – число витков обмотки катушки. Когда вращающий момент равен противодействующему, катушка неподвижна. При этом  = BswI/W = S_II, где S_I – чувствительность И.м.м. к току. При B = const угол  пропорционален току, причем знак этого угла зависит от направления тока.

При переменном токе i(t) вращающий момент зависит от времени t: M(t) = S_I i(t). Характер движения подвижной катушки зависит в этом случае от периода T ее собственных колебаний и спектра тока. Если И.м.м. предназначен для работы в цепях постоянного тока, то значение T обычно не менее одной секунды. При этом подвижная катушка практически не реагирует на гармоники i(t) с частотами 50 Гц и более, а угол  пропорционален среднему значению тока:  = S_I I_ср. Поэтому для построения, например, вольтметров аналоговых переменного тока на основе И.м.м. необходимо использовать преобразователи переменного напряжения в постоянный ток.

В зависимости от назначения используются различные конструкции И.м.м. с подвижной рамкой. В малогабаритных амперметрах и вольтметрах постоянного тока часто используется И.м.м. с внутрирамочным магнитом. В омметрах часто используют логометрический И.м.м. (см. логометр).

Если И.м.м. предназначен для работы в цепях переменного тока (в осциллографических и вибрационных гальванометрах), то его конструкция должна обеспечивать малую инерционность подвижной части. В настоящее время такие И.м.м. используются редко.

{2К5}

ИЗМЕРИТЕЛЬНЫЙ МЕХАНИЗМ ЭЛЕКТРОМАГНИТНЫЙ (electromagnetic measuring mechanism) – измерительный механизм, в котором вращающий момент возникает в результате взаимодействия магнитного поля неподвижной катушки с током и одним или несколькими подвижными ферромагнитными сердечниками.

Одна из конструкций И.м.э. представлена на рис. 1, где 1 – катушка с обмоткой из медного провода, 2 – эксцентрически укрепленный на оси 3 ферромагнитный сердечник. При постоянном токе I в катушке сердечник втягивается в катушку, поворачиваясь вокруг оси вместе с закрепленной на ней стрелкой. Противодействующий момент, пропорциональный углу поворота сердечника, создается спиральной пружиной. При переменном токе вращающий момент зависит от времени. Однако из-за большой инерционности подвижной части И.м.э. она не колеблется, если спектр тока не содержат гармоник с частотами, существенно меньшими 50 Гц, а ее положение определяется средним значением вращающего момента. При равенстве вращающего и противодействующего моментов  = 0,5(dL/d)I²/W, где  - угол поворота сердечника, L – индуктивность катушки, I – постоянный ток или действующее значение переменного тока, а W – удельный противодействующий момент.

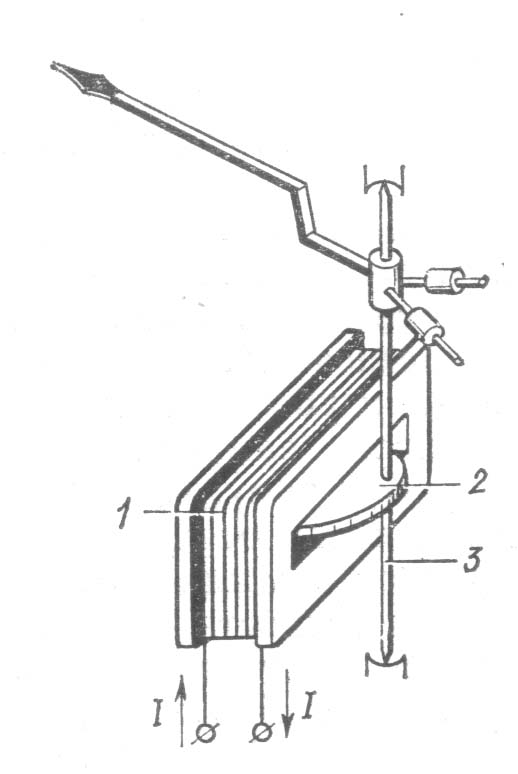
Рис. 1. Электромагнитный измерительный механизм.

И.м.э. используются для построения, амперметров и вольтметров постоянного и переменного токов (примерно до 10 кГц). Кроме того, логометрические И.м.э. (см. логометр) применяются в частотомерах.

{2К6}

ИЗМЕРИТЕЛЬНЫЙ МЕХАНИЗМ ЭЛЕКТРОДИНАМИЧЕСКИЙ (electrodynamic measuring mechanism) – измерительный механизм, в котором вращающий момент возникает в результате взаимодействия магнитных полей неподвижных и подвижных катушек с токами.

Принцип действия И.м.э. иллюстрирует рис. 1. Внутри неподвижной катушки 1 с током I₁ размещена укрепленная на растяжках подвижная катушка 2 с током I₂. B₁ и B₂ – векторы магнитной индукции в катушках 1 и 2. При постоянных токах вращающий момент M зависит от их произведения, а противодействующий M_пр, пропорционален углу  отклонения подвижной катушки: M_пр = W, где W = const – удельный противодействующий момент. При M = M_пр катушка неподвижна и  = (dM_1,2/d)I₁I₂/W, где M_1,2 – взаимная индуктивность катушек 1 и 2. При переменных токах в катушках вращающий момент зависит от времени. Однако из-за большой инерционности подвижной катушки она не колеблется, если спектры токов не содержат гармоники с частотами, существенно меньшими 50 Гц, а ее положение определяется средним значением вращающего момента. При синусоидальных токах  = (dM_1,2/d)I₁I₂cos/W, где  - угол фазового сдвига между токами в неподвижной и подвижной катушках, а I₁ и I₂ – действующие значения этих токов.

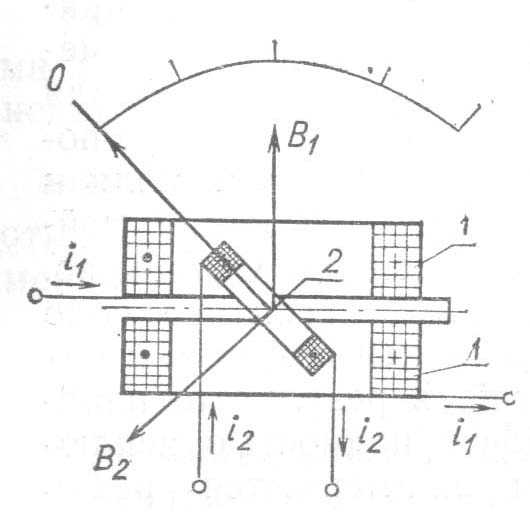
Рис. 1. Электродинамический измерительный механизм.

И.м.э. используются для построения вольтметров, амперметров и ваттметров постоянного и переменного токов (примерно до 10 кГц). Кроме того, логометрические И.м.э. применяются в частотомерах и фазометрах.

{2К7}

ИЗМЕРИТЕЛЬНЫЙ МЕХАНИЗМ ФЕРРОДИНАМИЧЕСКИЙ (cored electrodynamic measuring mechanism) – измерительный механизм, в котором вращающий момент возникает в результате взаимодействия магнитных полей неподвижных и подвижных катушек с токами, причем катушки имеют магнитопровод из магнитомягкого материала.

По принципу действия И.м.ф. не отличается от измерительного механизма электродинамического. Благодаря наличию магнитопровода ферродинамические приборы обладают большей чувствительностью и меньшим собственным потреблением энергии по сравнению с электродинамическими, на их показания мало влияют внешние магнитные поля, однако по точности они уступают электродинамическим.

{2К8}

ИЗМЕРИТЕЛЬНЫЙ МЕХАНИЗМ ЭЛЕКТРОСТАТИЧЕСКИЙ (electrostatic measuring mechanism) – измерительный механизм, в котором вращающий момент возникает в результате взаимодействия электрически заряженных электродов.

Одна из конструкций И.м.э. представлена на рис. 1, где 1 – электрически соединенные неподвижные электроды, 2 – подвижный электрод, укрепленный на оси вместе с указателем 3. При постоянном напряжении U между электродами подвижный электрод поворачивается. Противодействующий момент, пропорциональный углу поворота, создается спиральной пружиной. При переменном напряжении вращающий момент зависит от времени. Однако из-за большой инерционности подвижной части И.м.э. она не колеблется, если спектр напряжения не содержат гармоник с частотами, существенно меньшими 50 Гц, а ее положение определяется средним значением вращающего момента. При равенстве вращающего и противодействующего моментов  = 0,5(dC/d)U²/W, где  - угол поворота подвижного электрода, C – емкость между подвижным и неподвижным электродами, U – постоянное или действующее значение переменного напряжения, а W – удельный противодействующий момент.

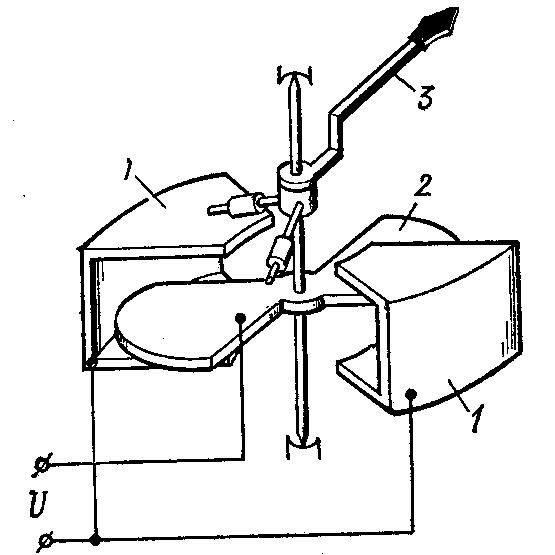
Рис.1. Электростатический измерительный механизм.

И.м.э. используются для построения вольтметров с верхними пределами измерений примерно от 10 В до 100 кВ и частотным диапазоном до 10 МГц.

{2К9}

ДЕЛИТЕЛЬ НАПРЯЖЕНИЯ (voltage divider) - преобразователь напряжения постоянного или переменного тока в такое же напряжение, но меньшее по размеру в строго определённое число раз. Простейший Д.н. – это два последовательно соединённые резистора R₁ и R₂ (два плеча делителя), на которые подаётся входное напряжение U_вх и с одного из которых, например, с R₂ снимается выходное напряжение U_вых. Коэффициент преобразования (деления) при отсутствии нагрузки определяется формулой

К = U_вых/U_вх = R₂/(R₁ + R₂).

Отклонения значений R₁ и R₂ от номинальных обусловливает соответственно отличие К от номинала, т.е. погрешность делителя. В точных Д.н. применяют резисторы с малым температурным коэффициентом сопротивления и высокой временной стабильностью, например, из манганиновой проволоки. Нагрузка, подключаемая параллельно R₂, в частности, входное сопротивление последующего звена измерительной цепи, влияет на К тем меньше, чем меньше выходное сопротивление делителя

R_вых = R₁ R₂/(R₁ + R₂)

и чем больше сопротивление нагрузки. Если нагрузка постоянна, то она может быть учтена при определении номинального коэффициента преобразования, но изменения нагрузки вызывают погрешность. Требование малого R_вых находится в противоречии с требованием большого входного сопротивления R_вх = R₁ + R₂, что соответствует малой погрешности от взаимодействия делителя с источником измеряемого напряжения. На переменном токе к Д.н. может предъявляться требование не только близости коэффициента преобразования к номиналу, но и синфазности выходного напряжения со входным (сдвиг фаз может возникать из-за остаточных реактивностей резисторов, особенно на высоких частотах).

Д.н. могут быть не только однопредельными, т.е. с одним номинальным коэффициентом преобразования, но и многопредельными, а также не только с постоянным, но и с регулируемым отношением плеч (плавно, дискретно или комбинированно). Обычный магазин сопротивлений с отводами от одной или нескольких декад можно использовать в качестве делителя напряжения с дискретно регулируемым в широком диапазоне значением коэффициента преобразования.

На переменном токе кроме резистивных Д.н. используются также индуктивные и емкостные. Индуктивные делители на низких и средних частотах позволяют получить более высокую точность, чем резистивные. Например, у делителя на тороидальном сердечнике из пермаллоя отличие действительноых коэффициентов деления от номинальных, определяемых отношением чисел витков обмоток, может быть 0,001 % и менее. Емкостные Д.н. применяют для деления высоких напряжений. Д.н. входят в состав многих средств измерений в качестве звена измерительной цепи. Например, резистивные Д.н. с номинальными значениями коэффициента деления 10, 100, и 1000 применяются во входных цепях многопредельных аналоговых и цифровых вольтметров. Кроме того, Д.н. выпускают как самостоятельные изделия с нормированными метрологическими характеристиками, т.е. как измерительные преобразователи.

{2К10}

ГАЛЬВАНОМЕТР (galvanometer) - электроизмерительный прибор с высокой чувствительностью к току и напряжению, имеющий неградуированную шкалу. Г. строятся на основе измерительных механизмов магнитоэлектрических и используются для измерения малых постоянных токов и напряжений, количеств электричества, для измерения и регистрации переменных токов, а также в качестве нуль-индикаторов в цепях постоянного и переменного тока.

В цепях постоянного тока обычно используются переносные и стационарные Г. с подвижной рамкой. Переносные Г. имеют встроенную шкалу, а стационарные - выносную, что обеспечивает более высокую чувствительность. Цена деления шкалы по току для наиболее чувствительных стационарных Г. составляет примерно 10^-11 А, по напряжению - 10^-8 В, а для переносных соответственно 10^-9 А и 10^-6 В. Допускается отклонение значения цены деления от указанной в паспорте на Г. от 0,5 до 10%. Время установления показаний Г. зависит от особенностей его конструкции и сопротивления внешней цепи, на которую замкнута обмотка рамки Г. Регулируя сопротивление внешней цепи, можно устанавливать один из трех возможных режимов работы Г.: колебательный, критический или апериодический. Наименьшее время установления обеспечивает колебательный режим, близкий к критическому.

Если через обмотку рамки Г., работающего в колебательном режиме, пропустить импульс тока, длительность которого много меньше периода свободных колебаний подвижной части Г., то первое наибольшее отклонение указателя будет пропорционально количеству электричества, протекшему через обмотку. Для того, чтобы наибольшее отклонение указателя мало зависело от длительности импульса, увеличивают момент инерции подвижной части Г., увеличивая тем самым период свободных колебаний примерно до 20 с. Такие Г. называют баллистическими. У наиболее чувствительных баллистических Г. цена деления шкалы составляет примерно 10^-9 Кл. Чувствительность баллистических Г. зависит от сопротивления внешней цепи, поэтому ее необходимо определять экспериментально. Баллистические Г. используются для измерения магнитных потоков.

В качестве нуль-индикаторов в цепях переменного тока в диапазоне частот от 30 до 100 Гц используют вибрационные Г. Подвижная часть такого Г. состоит из укрепленных на растяжках маленького постоянного магнита и зеркальца. Подвижный магнит находится под действием магнитного поля вспомогательного постоянного магнита и переменного магнитного поля, создаваемого электромагнитом, по обмотке которого протекает входной ток Г. Под действием переменного магнитного поля подвижный магнит вместе с зеркальцем колеблется, причем амплитуда колебаний зависит не только от значения тока, но и от его частоты. При равенстве этой частоты частоте собственных колебаний подвижной части (резонансный режим) амплитуда колебаний максимальна. При этом максимальна ширина световой полосы, которую создает луч света, отраженный от зеркальца, на шкале Г. Чувствительность вибрационных Г. сильно зависит от частоты входного тока. Цена деления шкалы вибрационных Г. составляет примерно 10^-7 А по току и 10^-5 В по напряжению.

Для регистрации и измерения переменных токов в осциллографах светолучевых используются Г. с малым моментом инерции подвижной части – осциллографические Г. Рабочая полоса частот таких Г. лежит в пределах от 0 до 10 кГц.

{2К11}

ВОЛЬТМЕТР АНАЛОГОВЫЙ (analog voltmeter) – вольтметр, у которого результат измерения определяют по положению указателя на шкале. По элементной базе В.а. разделяются на электромеханические и электронные.

Основу электромеханических образуют измерительные механизмы – магнитоэлектрические, электромагнитные, электродинамические, ферродинамические, электростатические. Магнитоэлектрические В.а. – милливольтметры и вольтметры – предназначены для измерения постоянного напряжения. У них последовательно с обмоткой измерительного механизма включён добавочный резистор из материала, сопротивление которого мало зависит от температуры (сплав манганин). Чем больше верхний предел диапазона измерения, тем больше сопротивление добавочного резистора и тем меньше температурная погрешность прибора, обусловленная температурными изменениями сопротивления обмотки из медного провода. У милливольтметров добавочный резистор может вовсе отсутствовать, и тогда принимают меры для компенсации температурной погрешности, в частности, применяют термозависимые магнитные шунты, повышающие магнитную индукцию в воздушном зазоре магнитопровода с ростом температуры. Переносные приборы имеют классы точности 0,1; 0,2 и 0,5. Обычно они имеют несколько переключаемых пределов измерения. Щитовые приборы обычно однопредельные и имеют классы точности 1,0 и 1,5.

Стремление использовать высокую чувствительность магнитоэлектрического измерительного механизма и снять ограничение, связанное с тем, что он не работает на переменном токе, привело к созданию магнитоэлектрических приборов с преобразователями переменного напряжения в постоянное – выпрямительных и термоэлектрических. У выпрямительных В.а. (преобразователи на полупроводниковых диодах) частотный диапазон достигает обычно нескольких десятков килогерц, у термоэлектрических (преобразователи на основе термопары с нагревателем) - нескольких мегагерц. Классы точности этих В.а. обычно не выше 1,0; диапазон измерения – от долей вольта до 600 В. Чаще всего выпрямительные приборы выпускают универсальными, т.е. способными работать как на переменном, так и постоянном токе (при этом преобразователь отключен) и комбинированными, т.е. предназначенными для измерения не только напряжений, но и токов, а иногда и сопротивлений. Универсальные и комбинированные приборы имеют разные шкалы для разного рода измеряемых величин.

Электромагнитные, электродинамические и ферродинамические В.а. предназначены для измерения действующего значения переменного напряжения, причём их показания не зависят от формы кривой напряжения, если его спектр не выходит за пределы частотного диапазона прибора. Они могут измерять и постоянное напряжение, причём показания электродинамических приборов принципиально одинаковы на постоянном и переменном токе, если постоянное напряжение равно действующему значению переменного. Это позволяет обеспечивать высшие классы точности 0,1 и 0,2 у этих приборов, так как их можно точно проградуировать на постоянном токе, а применять на переменном. Показания электромагнитных и ферродинамических В.а. немного различаются при измерении постоянного и переменного напряжения из-за потерь энергии в магнитопроводе на перемагничивание и на вихревые токи. Классы точности этих приборов обычно не выше 0,5. У электромагнитных В.а. последовательно с обмоткой включён добавочный резистор. Для того, чтобы температурная погрешность не выходила за допускаемые пределы, отношение сопротивления добавочного резистора из манганина к сопротивлению обмотки из меди не должно быть меньше определённого значения. Поэтому у вольтметров на малые пределы измерения уменьшают сопротивление катушки, т.е. уменьшают число витков, увеличивая тем самым ток полного отклонения указателя “на всю шкалу”. У электро- и ферродинамических в.а. обе обмотки (подвижная и неподвижная) и добавочный резистор включены последовательно. Для измерения напряжений выше 600 В применяют измерительные трансформаторы напряжения. Верхняя граница частотного диапазона названных В.а. не превышает нескольких килогерц.

Электростатические В.а. существенно отличаются от остальных. Добавочный резистор у них отсутствует, измеряемое напряжение прикладывается непосредственно между подвижной и неподвижной пластинами измерительного механизма. Электростатические вольтметры на разные пределы измерения отличаются друг от друга расстоянием между пластинами: оно тем больше, чем на большее напряжение рассчитан вольтметр. Электростатический измерительный механизм используется для построения не только вольтметров, но и киловольтметров. Верхняя граница частотного диапазона электростатических вольтметров достигает единиц мегагерц. Это объясняется тем, что вращающий момент в электростатическом измерительном механизме зависит от напряжения, а не от тока (как в электромагнитном, электро- и ферродинамическом), уменьшающегося с ростом частоты из-за возрастания индуктивного сопротивления обмоток. Входное сопротивление электростатических вольтметров очень велико – это сопротивление изоляции между пластинами, входная ёмкость – единицы пикофарад.

Основу электронных В.а. составляют усилители и выпрямители с магнитоэлектрическим измерительным механизмом на выходе. В зависимости от взаиморасположения усилителя и выпрямителя образуются две простейших структурных схемы: усилитель – выпрямитель – магнитоэлектрический измерительный механизм (У – В – М) и выпрямитель – усилитель – магнитоэлектрический измерительный механизм (В – У – М). В первой схеме применяют усилитель переменного напряжения и двухполупериодный выпрямитель на диодах, а во второй – амплитудный детектор и усилитель постоянного напряжения. В.а., построенные по этим двум схемам, существенно различаются по своим свойствам. Усилитель в схеме У – В – М обеспечивает высокую чувствительность и ограничивает частотный диапазон на уровне нескольких мегагерц. В.а., соответствующие этой схеме, предназначены для измерения только переменного напряжения и обычно имеют переключаемые верхние пределы диапазонов измерения 1 мВ; 3 мВ; 10 мВ; 30 мВ; 100 мВ; 300 мВ; 1 В; 3 В; 30 В; 100 В; 300 В. На верхних пределах используется делитель напряжения, на нижних изменяется коэффициент усиления. В.а., со схемой В – У – М имеют гораздо меньшую чувствительность (верхний предел от 0,3 до 1 В на нижнем диапазоне), но более широкий частотный диапазон (до гигагерц), ограниченный выпрямителем. Обычно эти В.а. являются универсальными: при отключении выпрямителя они позволяют измерять постоянное напряжение. Высокое входное сопротивление – мегаомы – характерно для обеих схем, а входная ёмкость второй схемы – несколько пикофарад – меньше, чем у первой. У первой схемы она определяется не только входной ёмкостью усилителя, но и ёмкостью кабеля, которым В.а. присоединяется к источнику измеряемого напряжения. У второй схемы выпрямитель, построенный по схеме амплитудного детектора, помещается в выносной головке, и ёмкость кабеля, которым она соединена с остальной частью вольтметра, не имеет значения, потому что по нему передаётся постоянное напряжение. Шкалы В.а., построенных по обеим схемам, проградуированы в действующих значениях для синусоидального измеряемого напряжения, но В.а. по схеме В –У –М обычно реагирует на средневыпрямленное значение измеряемого напряжения, а У – В – М – на амплитудное, поэтому оба вольтметра могут правильно работать только при синусоидальном измеряемом напряжении.

Особую группу составляют импульсные В.а. Они тоже построены по схеме В – У – М, но их шкалы проградуированы в максимальных значениях измеряемого напряжения. В.а., позволяющие измерять действующие значения напряжения независимо от формы кривой, имеют более сложные схемы по сравнению с рассмотренными. Электронные В.а. по сравнению с электромеханическими имеют более высокую чувствительность, более широкий частотный диапазон, большее входное сопротивление и меньшую точность: пределы основной приведённой погрешности обычно не меньше  2,5 %. {2К12}

Подобные проблемы возникают при работе не только с аналоговыми электронными вольтметрами, но и с другими электронными средствами измерений, например, с электронно-лучевыми аналоговыми и цифровыми осциллографами и цифровыми вольтметрами. Наиболее радикально эти проблемы решаются двумя способами:

- путем использования во входных цепях электронных средств измерений дифференциальных измерительных усилителей;

- путем использования схем гальванического разделения между входными и выходными цепями средств измерений с электростатическим экранированием входных цепей.

При этом средство измерений имеет 3 входных зажима: «землю» (или зажим электростатического экрана) и 2 зажима, на которые подается измеряемое напряжение (например, U₅₄ на схеме рис. 2.6). При правильном подключении средства измерений паразитные токи не создают падений напряжений, искажающих измеряемое напряжение.

{2К13}

КОМПЕНСАТОР (compensator, potentiometer) - средство измерений, основанное на применении нулевого метода измерения. Нулевой метод измерения является разновидностью метода сравнения с мерой, когда результирующий эффект воздействия величин на компаратор доводят до нуля. Наибольшее распространение получили К. (синоним - потенциометры) для измерения напряжения. Различают К. постоянного и переменного тока. Принцип действия К. постоянного тока иллюстрирует рисунок:

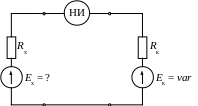
Источники измеряемого и компенсирующего сигналов представлены соответственно в виде эквивалентных генераторов ЭДС E_X и E_К и внутренних сопротивлений R_X и R_К. Компенсирующая ЭДС E_К изменяется до тех пор, пока компаратор (нуль-индикатор НИ) не зафиксирует равенства E_X = E_К, которое является функцией преобразования К. при идеальном компараторе. Из этого равенства следует, что точность К. определяется точностью ЭДС и не должна зависеть от величин R_X и R_К. Приведенная погрешность E_К снижается вплоть до 0,001 % благодаря применению точной меры ЭДС - нормального элемента. Относительную погрешность измерения E_X по отношению к E_К удается уменьшить благодаря прецизионным делителям напряжения до 0,0001 %.

К . переменного тока должны иметь две регулировки компенсирующего напряжения. В зависимости от вида регулировок различают полярно-координатные и прямоугольно-координатные К. В первом случае регулируется амплитуда и фаза, во втором - амплитуды сдвинутых на 90 напряжений. Поскольку на переменном токе нет столь точных мер напряжения, как на постоянном, то абсолютная точность измерения на переменном токе ниже и обычно характеризуется классом точности не лучше 0,1.

В связи с успехами построения прецизионных аналого-цифровых преобразователей удалось достигнуть примерно той же точности измерения на постоянном и переменном токе с помощью цифровых электроизмерительных приборов, которые вытеснили К. с ручным уравновешиванием. Однако идея уравновешивания, показанная на рис. 1, широко используется на практике, например, в аналого-цифровых преобразователях с последовательным приближением.

{2К14}

ВОЛЬТМЕТР ЦИФРОВОЙ (voltmeter digital) - вольтметр, выполняющий автоматическое преобразование измеряемого напряжения в цифровой код, в соответствии с которым на цифровом отсчетном устройстве (ЦОУ) индицируется результат измерения. В большинстве современных В.ц., кроме того, предусматривается вывод напряжений – носителей кода на специальный выходной разъем. Это дает возможность передать код в какое-либо устройство обработки измерительной информации, например, в персональную ЭВМ, на цифровую печать и т. д. Автоматическое преобразование измеряемого напряжения В.ц. в код осуществляет аналого-цифровой преобразователь (АЦП). Кроме указанных функциональных узлов, В.ц. содержат предварительные аналоговые преобразователи (АП), предназначенные для изменения масштаба входного напряжения или его преобразования в другую физическую величину, более удобную для кодирования выбранным методом.

К основным техническим характеристикам В.ц. относят: диапазон измерений, чувствительность, разрешающую способность, входное сопротивление, входной ток, точность, помехозащищенность и быстродействие. Обычно общий диапазон измерений делится на несколько поддиапазонов, для которых указывают номинальные значения. Чувствительность определяется как цена единицы младшего разряда. Разрешающей способностью называют величину, обратную числу “ступеней” цифровой шкалы на поддиапазоне. Входное сопротивление В.ц. характеризует его потребление от источника измеряемого напряжения. Точность В.ц. количественно оценивается погрешностью.

В нашей стране для В.ц. нормируют предельное значение относительной погрешности (в процентах) по формуле  = c+d(U_ном/U  1) , где c и d – постоянные числа, %; U_ном – номинальное значение напряжения на данном поддиапазоне; U–значение измеряемого напряжения. Под помехами понимают паразитный сигнал, действующий на входе В.ц. вместе с измеряемым напряжением и искажающий результат измерения, а под помехозащищенностью – способность В.ц. уменьшать влияние помех на результат измерения. Быстродействие В.ц. характеризуется длительностью одного цикла измерения или количеством измерений в секунду.

По роду измеряемой величины В.ц. подразделяют на вольтметры постоянного и переменного тока. В.ц. постоянного тока (В.ц. ПТ) образуют самую большую группу вольтметров. Вольтметры переменного тока в подавляющем большинстве случаев строят на основе В.ц. ПТ, дополненных преобразователем переменного напряжения в постоянное. Технические характеристики В.ц. ПТ во многом определяются методом преобразования напряжения в код.

В современных В.ц. преимущественное распространение получил метод время-импульсного интегрирующего преобразования, который предполагает предварительное преобразование среднего значения измеряемого напряжения в интервал времени с последующим кодированием последнего. Этот метод имеет ряд разновидностей, среди которых самым распространенным является метод двухтактного интегрирования.

При двухтактном интегрировании на первом такте выполняется интегрирование измеряемого напряжения за фиксированный интервал времени t_1, затем на втором такте выполняется интегрирование опорного напряжения U_0, знак которого противоположен знаку U, до тех пор, пока результирующий интеграл не станет равным нулю. Интервал времени t₂ интегрирования U₀ пропорционален значению U:

U = U₀t₂/t₁.

Интервал t₂ заполняется импульсами генератора образцовой частоты, количество которых, подсчитанное счетчиком, дает код значения U.

Длительность интервала t₁ выбирается равной или кратной периоду наиболее часто встречающейся помехи – периоду напряжения промышленной сети. За счет этого обеспечивается высокая помехоустойчивость В.ц. ПТ, реализующих метод двухтактного интегрирования.

На практике, кроме напряжения постоянного тока, часто возникает необходимость измерять другие величины – переменные напряжения, постоянный и переменный ток, сопротивление постоянному току и т.д. Многофункциональные цифровые приборы – мультиметры (М) выполняют на основе В.ц. ПТ, дополненных преобразователями измеряемых величин в напряжение постоянного тока. Такие преобразователи иногда выполняют в виде сменных блоков. При измерении переменного напряжения в мультиметрах применяют преобразователи среднего по модулю и среднеквадратического (действующего) значений.

По области применения В.ц. и М подразделяются на лабораторные, системные и щитовые.

Современные модели В.ц. и М по точности и разрешающей способности близки к практическим пределам. Например, погрешности наиболее точных зарубежных и отечественных моделей В.ц. и ЦМ близки к погрешностям государственных эталонов. Так точность В.ц. ПТ модели 7081 фирмы Солартрон характеризуется погрешностями (0,0005% U +0,00006% от U_ном) в течение трех месяцев работы после калибровки. Разрешающая способность В.ц. ПТ фирмы Дэтрон равна 10^8.

Помимо высоких метрологических показателей современные В.ц. и ЦМ характеризуются расширенными функциональными возможностями: позволяют, например, выполнять арифметические операции над результатами измерений, статистически их обрабатывать и т.д. Оба направления технического совершенствования В.ц. и ЦМ связаны с применением встроенных микро-ЭВМ, выполненных на основе средств микропроцессорной техники: микропроцессоров и однокристальных микроконтроллеров. Использование микропроцессорной техники дало возможность усовершенствовать известные и создать новые структурные и схемотехнические решения, позволившие проектировать надежные и технологичные приборы с высокими метрологическими и сервисными характеристиками.

{2К15}

АНАЛОГО-ЦИФРОВОЙ ПРЕОБРАЗОВАТЕЛЬ (АЦП, analog-to-digital converter) - устройство для автоматического преобразования непрерывных величин в значения числовых кодов. АЦП преобразует непрерывную по времени и значениям физическую величину (аналоговый сигнал) в последовательность числовых кодов (цифровой сигнал), осуществляя при этом три основные операции: дискретизацию по времени, квантование по значениям и кодирование. АЦП широко используются в качестве функциональных блоков средств измерений (цифровых электроизмерительных приборов, измерительно-вычислительных комплексов и т.д.), а также других устройств и систем (например, систем цифровой обработки речевых сигналов).

Аналоговый сигнал на входе АЦП может иметь различную физическую природу. Это может быть температура, давление, перемещение, электрическое напряжение, ток, мощность, сопротивление и т.д. В подобных случаях АЦП состоит обычно из двух основных узлов: аналогового преобразователя входной величины в электрическое напряжение, мгновенные значения которого пропорциональны значениям входного сигнала, и АЦП этого напряжения. Поэтому часто под АЦП подразумеваются измерительные преобразователи электрического напряжения в цифровой сигнал.

Современные АЦП выполняются по микроэлектронной технологии. В их состав часто входят вспомогательные узлы, существенно улучшающие метрологические характеристики и расширяющие функциональные возможности АЦП: буферные усилители, автоматические переключатели диапазонов, программируемые усилители, устройства выборки и хранения напряжения, схемы автокалибровки, цифровые оперативные и постоянные запоминающие устройства, цифровые фильтры, устройства предварительной цифровой обработки данных и т.п. Практически все современные АЦП ориентированы на совместную работу с микропроцессорными системами и содержат элементы интерфейса: буферные регистры, дешифраторы адреса и т.п.

Зависимость значений числовых кодов на выходе АЦП от напряжения на его входе устанавливает характеристика преобразования (ХП). Номинальная ХП представляет собой ступенчатую кривую, ширина каждой ступеньки которой постоянна и равна единице младшего разряда (кванту), а высота соответствует приращению кода на единицу. В технической документации обычно задается диапазон преобразования АЦП и количество двоичных разрядов, равное двоичному логарифму от номинального числа возможных различных кодовых комбинаций на выходе АЦП; эти данные позволяют определить номинальную ХП АЦП, а также его номинальный коэффициент преобразования, определяемый тангенсом угла наклона к оси абсцисс прямой, проведенной через начальную и конечную точки номинальной ХП АЦП. Значение единицы младшего разряда характеризует разрешающую способность АЦП, а количество двоичных разрядов позволяет судить о его точности.

Погрешности (П) АЦП характеризуют различия между номинальной и действительной ХП. Определение П сводится к определению напряжений межкодовых переходов (НМП) - значений напряжения на входе АЦП, соответствующих переходу от предыдущего к заданному значению выходного кода. П АЦП в заданной точке ХП называют обычно разность между действительным и номинальным значениями НМП.

Нормируют следующие основные составляющие П: напряжение смещения нуля - аддитивную П АЦП, П коэффициента преобразования - мультипликативную П АЦП, П дифференциальной линейности, П линейности (нелинейность). Первые две составляющие несущественны для ряда областей применения АЦП и, кроме того, могут быть значительно уменьшены путем аддитивной и мультипликативной коррекции.

П дифференциальной линейности (дифференциальной нелинейностью) называется разность между действительным и средним значением кванта АЦП; она определяет два важных свойства АЦП: непропадание кодов и монотонность ХП (при изменении входного напряжения от начальной до конечной точки диапазона преобразования на выходе АЦП должны последовательно возникать все возможные кодовые комбинации).

П линейности (нелинейность, интегральная нелинейность) - нелинейная составляющая П АЦП - позволяет оценить нелинейные искажения сигнала при аналого-цифровом преобразовании.

Кроме приведенных выше, нормируются и другие технические характеристики АЦП - отношение сигнал-шум, зависимости ХП от времени, температуры и напряжения питания, коэффициенты подавления помех, входное сопротивление, максимальное число преобразований в секунду и т.д. Важнейшей динамической характеристикой АЦП является время преобразования - интервал времени от начала скачкообразного изменения входного напряжения до момента установления кода на его выходе с заданной точностью.

Разработано много типов АЦП, различающихся по принципу действия, точности, быстродействию, способности подавлять помехи и другим характеристикам: параллельные, последовательного приближения, параллельно-последовательные, с промежуточным преобразованием в интервал времени или частоту, с сигма-дельта модуляцией и др. Параллельные АЦП реализуют метод считывания и обладают наибольшим быстродействием (до 10⁸ - 10⁹ преобразований в секунду). Однако количество двоичных разрядов n такого АЦП обычно не превышает 10. Это связано с особенностью его схемы, в которую должен входить набор компараторов{2К16} напряжения, число которых примерно равно 2ⁿ (для 10-разрядного АЦП требуется более 1000 компараторов).

АЦП последовательного приближения (ПП), упрощенная схема которого представлена на рис. 1, реализует компенсационный метод измерений напряжений (см. {2К13}). Входное напряжение сравнивается последовательно с набором образцовых напряжений, вырабатываемых цифроаналоговым преобразователем ЦАП, управляемым логической схемой ЛС. Сравнивающее устройство СУ (компаратор) определяет знак разности входного и образцового напряжений и передает эту информацию ЛС, которая формирует для ЦАП команды на увеличение или уменьшение образцового (компенсирующего) напряжения. Время преобразования (t_пр) АЦП ПП обычно не менее 10 мкс, n  16.

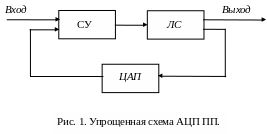
Большим быстродействием (t_пр = 1 - 5 мкс) обладают параллельно-последовательные АЦП. В таких АЦП входное напряжение сначала преобразуется в код старших разрядов вспомогательным параллельным АЦП, управляющим образцовым ЦАП. Полученное образцовое напряжение вычитается из входного, разность этих напряжений усиливается и преобразуется вторым вспомогательным АЦП в код младших разрядов.

АЦП с предварительным преобразованием напряжения в частоту или интервал времени широко применяются в цифровых вольтметрах и мультиметрах. Они обладают высокой точностью и способностью подавлять помехи, но малым быстродействием (обычно t_пр  20 мс). В ряде областей применения эти АЦП вытесняются более современными сигма-дельта АЦП, обладающими примерно такими же точностью и быстродействием, но более широкими функциональными возможностями, способностью работать со сравнительно высокочастотными сигналами и более эффективно подавлять помехи. Например, 24-разрядный 5-канальный сигма-дельта АЦП типа AD7714 фирмы Analog Devices имеет программируемые усилители и цифровой фильтр, трехпроводный последовательный интерфейс; коэффициент подавления синфазных помех промышленной частоты у этого АЦП не менее 150 дБ, помех нормального вида - не менее 100 дБ, нелинейность не хуже 0,0015 %, частота выдачи данных - до 1 кГц.

{2К16}

КОМПАРАТОР (comparator) - устройство сравнения параметров двух сигналов. Синонимами являются понятия "прибор сравнения", "схема сравнения", "сравнивающее устройство", "индикатор баланса", "нуль-орган" и др. Различают цифровые и аналоговые К. Первые используются для сравнения кодов, а вторые - для сравнения информативных параметров двух сигналов. Аналоговые К. (измерительные приборы сравнения) разработаны для сравнения многих физических величин: веса (рычажные весы), длины (К. для линейных мер) и т.д.

Наибольшее распространение получили К. напряжений, которые с 60-ых годов выпускаются в виде интегральных схем. К. напряжений обычно имеют дифференциальный вход. При этом информативным параметром входного напряжения является разность напряжений на неинвертирующем и инвертирующем входах К. (U_вх.диф), а их полусумма (синфазное входное напряжение) является неинформативным параметром входного напряжения. Выходное напряжение обычно предусматривает согласование с определенным видом логических схем. Для этого U_вых.max - максимальное выходное напряжение К. - должно несколько превышать уровень логической единицы U¹, а U_вых.min - минимальное выходное напряжение К. - должно быть несколько меньше уровня логического нуля U⁰. Например, для логических схем типа ТТЛ (транзисторно-транзисторная логика) U¹  2,4 В, U⁰  0,4 В.

Идеальная функция преобразования К. с дифференциальным входным напряжением U_вх.диф показана на рис. 1 и описывается уравнением U_вх.диф = 0 при U⁰ U_вых U¹.

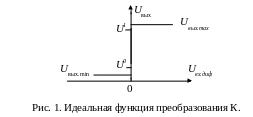
Для реального компаратора U_вх.диф  0 в диапазоне U⁰ U_вых U¹ и является функцией выходного напряжения, синфазного входного напряжения и других величин, которые можно рассматривать как влияющие величины. Примерно такая же функция преобразования типична и для операционного усилителя. Отличия могут состоять в различных диапазонах выходного напряжения и выходного тока, которые для операционного усилителя обычно симметричны относительно общей точки ("земли"). Однако эти отличия не очень существенны, особенно для прецизионных устройств с малым значением U_вх.диф. Важнее отличия динамических характеристик. Определяющим параметром компаратора является время восстановления после перегрузки (от сотен до долей наносекунд), от которого зависит время преобразования аналого-цифровых преобразователей с последовательным приближением и параллельного типа. Быстродействующие К. снабжаются стробирующим устройством с триггером-защелкой. При подаче стробирующего сигнала на выходе компаратора после окончания переходного процесса устанавливается напряжение, соответствующее полярности входного дифференциального напряжения в момент подачи строба. В подобных К. удается снизить апертурную задержку до уровня менее 1 нс. Соответственно появляется возможность уменьшить примерно до того же уровня такую важнейшую динамическую характеристику средств измерений с данным К, как время датирования.

{2К17}

ИНДУКТИВНОСТИ ИЗМЕРЕНИЕ (measurement of inductance) – измерение физической величины, характеризующей основной параметр индуктивной катушки  индуктивность. Возможные значения индуктивности L_х катушек колебательных контуров, дросселей, обмоток трансформаторов и электрических машин лежат в пределах примерно от 1 нГн до 10 кГн. Различные методы и средства измерения L_х обеспечивают предельные значения погрешности от тысячных долей до десятков процентов. Государственный эталон индуктивности воспроизводится с погрешностью порядка 10^-3 %.

Простейший способ И.и. – использование зависимости переменного тока или напряжения в какой-либо ветви от значения измеряемой индуктивности

Резонансный метод измерения – основан на применении высокочастотного генератора Г с LC-контуром которого слабо связан – через ёмкость С_р (рис. 1) или индуктивно – измерительный контур с опорным конденсатором с ёмкостью С₀ и измеряемой индуктивностью L_х. Изменением ёмкости С генератор настраивают в резонанс с собственной частотой f измерительного контура по максимальному показанию электронного вольтметра V. При фиксированном значении С₀ конденсатор с ёмкостью С можно снабдить шкалой в значениях индуктивности L_х. Другой вариант: при фиксированной частоте генератора измерительный контур настраивают в резонанс с помощью опорного конденсатора переменной ёмкости С₀, снабжённого шкалой в значениях L_x.

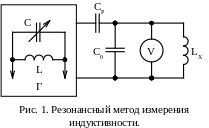
Разновидностью резонансного является генераторный метод измерения. В нём используются два идентичных высокочастотных генератора Г₁ и Г₂ (рис. 2). В контур Г₁ включён опорный конденсатор переменной ёмкости С₀, а в контур Г₂ последовательно с его индуктивной катушкой – катушка с измеряемой индуктивностью L_х. До подключения катушки с индуктивностью L_х генераторы настраивают на одинаковую частоту по нулевым биениям, выделяемым с помощью смесителя См, низкочастотного фильтра Ф, усилителя У и индикатора (телефон Т и магнитоэлектрический прибор, подключённый через выпрямитель В). При подключении L_х исчезнувшие нулевые биения восстанавливают изменением С₀. Если установить С₀ на условный нуль при начальной настройке, то при втором получении нулевых биений индуктивность L_х будет равна отсчёту по шкале С₀. Эти методы применяются для измерения малых индуктивностей (до единиц миллигенри) на высокой частоте (до сотен мегагерц); на низких частотах резонансный эффект слабо выражен.

Наиболее точное измерение индуктивности обеспечивает мостовой метод измерения. Применяются уравновешиваемые измерительные мосты переменного тока, в простейшем случае четырёхплечие. В диагональ питания моста подаётся синусоидальное напряжение, частота которого обычно составляет 1 кГц или 100 Гц, но иногда бывает и существенно более высокой. В одно из плеч включается катушка с измеряемой индуктивностью L_х и сопротивлением R₁( комплексное сопротивление этого плеча обозначим Z₁), в три других – в общем случае три комплексных сопротивления Z₂, Z₃ и Z₄ (Z₂ и Z₄ – смежные с Z₁, Z₃ – противоположное). Для равновесия моста необходимы два условия: z₁z₃ = z₂z₄ и φ₁ + φ₃ = φ₂ + φ₄, где z₁÷ z₄ – модули Z₁÷ Z₄, φ₁÷ φ₄ – углы сдвига фаз между током и напряжением в Z₁÷ Z₄. Из этих условий следует, что: а) Z₂÷ Z₄ должны иметь минимум два регулируемых параметра; б) в двух плечах могут быть не комплексные, а чисто активные сопротивления, например, Z₂ = R₂ и Z₄ = R₄, а Z₃ – эквивалентное сопротивление параллельно соединённых резистора R₃ и конденсатора С (рис. 3). Обычно одновременно с L_х измеряется добротность катушки Q = 2πfL_х/R₁ (см. добротности измерение). Из условий равновесия моста легко получить формулу L_х = R₂R₄С. При уравновешивании вручную резисторы R₂ и R₃ регулируют поочерёдно, добиваясь каждый раз нового минимального показания нуль-индикатора НИ и приближаясь к нулевому показанию. Высокая чувствительность НИ обеспечивается применением усилителя с выпрямителем и магнитоэлектрическим прибором на выходе. На звуковых частотах иногда применяют телефон.

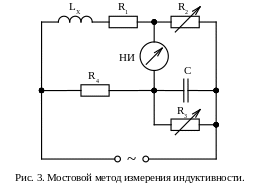
Наиболее высокую точность (погрешность до 0,001 %) обеспечивают трансформаторные мосты с тесной индуктивной связью плеч. Недостатком мостового метода измерения, особенно на высоких частотах, является отсутствие в мостах общей точки источника питания и НИ. Этого недостатка нет в двойных Т-образных мостах, но они являются частотозависимыми, т.е. при изменении частоты нарушается равновесие. В мостах с автоматическим уравновешиванием и цифровым отсчётом значений L_х (цифровые мосты) применяются разные способы управления регулируемыми элементами по двум каналам.

Обычно промышленность выпускает универсальные мосты, позволяющие измерять не только параметры индуктивных катушек, но и конденсаторов, а также сопротивления резисторов. Отечественные приборы, предназначенные для измерения только индуктивности обозначаются Е3, а универсальные – Е7.

{2К18}

ДОБРОТНОСТИ ИЗМЕРЕНИЕ (Q-factor measurement) – измерение безразмерной величины, характеризующей качество колебательных контуров или их элементов: индуктивных катушек и конденсаторов. Добротность колебательного LС-контура Q = (L/C)^0,5R^-1, где L – индуктивность катушки, С – ёмкость конденсатора, R = R_L + R_C – суммарное сопротивление потерь индуктивной катушки и конденсатора для эквивалентных схем с последовательным соединением активного и реактивного элементов. Добротность катушки Q_L = ωL/R_L, где ω – угловая частота; на резонансной частоте ω_р = (L C)^{- 0,5} она равна Q_L,р = (L/C)^0,5/R_L. Добротность конденсатора Q_C = (ωR_CC)^-1 на резонансной частоте равна Q_C,р = (L/C)^0,5/R_C, поэтому Q^-1 = (Q_L)^-1 + (Q_C)^-1. Обычно Q_C » Q_L, поэтому Q ≈ Q_L. Таким образом, Q легко найти, зная Q_L и Q_C (или только Q_L ), но можно и непосредственно измерить.

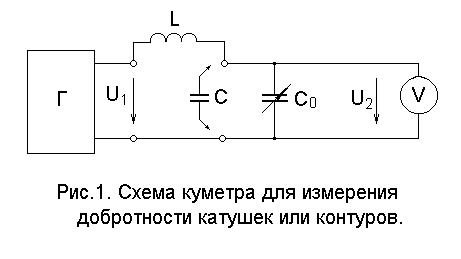
Существуют два основных метода Д.и. – резонансный и мостовой. Резонансный метод измерения применяется на высоких частотах (до сотен мегагерц). На нём основаны куметры – универсальные приборы для измерения добротности, индуктивности, ёмкости, резонансной частоты и др. параметров контуров колебательных. Куметр содержит три основных компонента (рис.1): генератор высокой частоты Г, измерительный контур с конденсатором переменной ёмкости С₀ и электронный вольтметр V.

При измерении Q_L исследуемая катушка с индуктивностью L и сопротивлением R включается последовательно с конденсатором С₀. Изменением С₀ добиваются резонанса, индицируемого по максимальному показанию вольтметра V. При этом U₂ ≈ U_1. Д.и. LС-контура Q проводят почти так же, но с тем отличием, что параллельно С₀ подключают ещё конденсатор исследуемого контура с ёмкостью С и устанавливают С₀ в положение минимальной ёмкости. Настройку в резонанс производят путем регулировки частоты напряжения генератора или емкости С. Добротность LС-контура можно определить и по-другому: путём измерения резонансной частоты ω_р и полосы пропускания контура Δω на относительном уровне 2^-0,5 и расчёта по формуле Q = ω_р /Δω.

Мостовой метод измерения позволяет измерить Q_L или tgδ = 1/ Q_C одновременно с индуктивностью L или, соответственно, с ёмкостью С

{2К19}

ВЗАИМНОЙ ИНДУКТИВНОСТИ ИЗМЕРЕНИЕ (measurement of mutual inductance) – измерение параметра М, характеризующего магнитную связь между двумя индуктивными катушками 1 и 2: е₂ = – Мdi₁/dt, где i₁ – ток в катушке 1; е₂ – эдс, наводимая в катушке 2 сцепленным с ней магнитным потоком, созданным током i₁. При синусоидальных i₁ и е₂ с частотой f и действующими значениями I₁ и Е₂ взаимную индуктивность М можно вычислить по показаниям амперметра, включённого последовательно с катушкой 1 и вольтметра с большим входным сопротивлением, подключённого к катушке 2: М = Е₂/ (2πfI₁).

Другой способ В.и.и.: если катушки 1 и 2 соединить последовательно и измерить индуктивность этого соединения, то при согласном включении (начало катушки 2 соединено с концом катушки 1 или конец катушки 2 с началом катушки 1) L_c = L₁ + L₂ + 2M, а при встречном (соединены начала или концы катушек) L_в = L₁ + L₂ – 2M. Измерив L_c и L_в, можно вычислить взаимную индуктивность: М = 0,25(L_c – L_в). При М « (L₁ + L₂) этот способ даёт большую погрешность. Этого недостатка лишён мостовой метод измерения, в котором используется схема, показанная на рис.

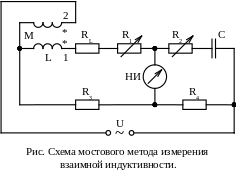
При равновесии моста, т.е. при нулевом показании нуль-индикатора НИ, достигаемого попеременными регулировками сопротивлений R₁ и R₂, взаимная индуктивность встречно включённых катушек 1 и 2 определяется формулами М = [(R₁ + R_L)R₄ – R₂ R₃]C и M = (R₂ + R₄)^-1[LR₄ + R₃(ω²C)^-1], где ω = 2πf – угловая частота напряжения питания моста U.

При этом должно выполнятся неравенство L > M, в противном случае катушки 1 и 2 можно поменять местами или добавить последовательно с катушкой 1 ещё одну с известным значением индуктивности. Из формул видно, что в общем случае для определения М нужно знать R_L катушки 1 или её индуктивность L, но при R₁ » R_L это не обязательно. Из второй формулы следует, что мост частотозависим, что является его недостатком: нужно знать частоту напряжения U, и любые её изменения влияют на результат измерения М. Этот недостаток устраняется при R₃ = 0, когда мост вырождается в более простую последовательно-параллельную цепь. При этом М = (R₁ + R_L)R₄C₂ (или М = R₁R₄C₂ при R₁ » R_L) и М = LR₄(R₂ + R₄)^-1.

Применяется также резонансный метод В.и.и. Схема содержит два контура: первый образован последовательным соединением источника синусоидального напряжения U, катушки 1 и конденсатора с ёмкостью С, а второй – последовательным соединением того же конденсатора, катушки 2 и вольтметра. Изменяя частоту f напряжения U, добиваются резонанса, при котором показание вольтметра минимально. При этом

М = (2πf)^–2 С^–1.

{2К20}

ЁМКОСТИ ИЗМЕРЕНИЕ (measurement of capacity) – измерение физической величины  ёмкости, характеризующей основной параметр электрического конденсатора (см. емкость электрическая). Практически измеряются емкости в диапазоне от 10^–15 до 1 Ф. Различные методы и средства измерения ёмкости обеспечивают предельные значения погрешности от 10^-3 до десятков процентов. Государственный эталон ёмкости воспроизводится с погрешностью порядка 10^-4 %. При некоторых методах измерения ёмкость измеряется одновременно с показателем качества конденсатора – тангенсом угла потерь.

Простейший способ Е.и. в диапазоне от 100 пФ до 10 мкФ – использование зависимости переменного тока или напряжения в какой-либо ветви от значения измеряемой ёмкости включённого в неё конденсатора. Другой метод Е.и. – метод заряда и разряда конденсатора (рис.1).

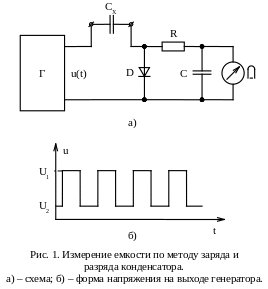
Магнитоэлектрическим прибором измеряется среднее значение I_ср тока разряда конденсатора с измеряемой ёмкостью С_х, перезаряжаемого импульсным напряжением u(t) с известной частотой f, поступающим от генератора Г: заряжается до напряжения U₁ через диод D и разряжается до напряжения U₂ через магнитоэлектрический прибор. Фильтр RC предотвращает нагрев подвижной части прибора переменной составляющей тока. Шкала прибора в значениях С_х получается равномерной: С_х = I_ср/f(U₁ - U₂), где U₁ и U₂ – соответственно напряжения, до которых заряжается и разряжается конденсатор. Пределы измерения от 100 пФ до 1 мкФ.

Метод дискретного счёта заключается в цифровом измерении интервала времени, равного постоянной времени τ цепи разряда конденсатора с измеряемой ёмкостью С_х через резистор с сопротивлением R₀. Для этого конденсатор С_х (рис. 2), заряженный до некоторого напряжения U, в момент t₁, задаваемый командой от устройства управления УУ, переключается от источника U на резистор R₀, а счётчик, входящий в состав цифрового измерителя интервалов времени ЦИИВ, начинает считать импульсы, поступающие на него с частотой f. Напряжение u_c на С_х (и на R₀) уменьшается по экспоненте и в момент t₂ достигает заданного уровня U/e, где е – основание натуральных логарифмов. Это фиксируется компаратором К и счёт прекращается. При этом t₂ – t₁ = τ = С_х R₀ =N/f, где N – количество импульсов, прошедших на счётчик, откуда С_х = N/(R₀f).

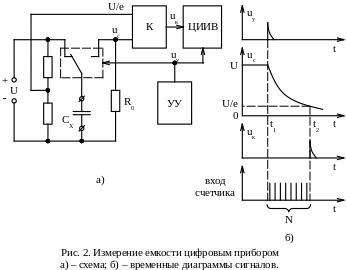
Метод наведения измерительной цепи вручную на резонанс – резонансный метод измерения – основан на применении высокочастотного генератора с LC-контуром которого слабо связан – индуктивно или через разделительный конденсатор С_р (рис.3) – измерительный контур с индуктивностью L₀ и измеряемой ёмкостью C_х. Изменением ёмкости С генератор настраивают в резонанс с собственной частотой f измерительного контура по максимальному показанию электронного вольтметра V. При фиксированном значении L₀ конденсатор С можно снабдить шкалой в значениях С_х. Метод применяется для измерения малых ёмкостей (не более 0,05 мкФ), погрешность измерения достигает 5 – 10 %. Её можно снизить до 1 % и менее, используя метод замещения. Для этого сначала вместо С_х подключают опорный конденсатор переменной ёмкости С₀ и при её максимальном значении С₀₁ настраивают генератор в резонанс. Затем параллельно С₀ включают С_х и уменьшением С₀ до некоторого значения С₀₂ восстанавливают резонанс. При этом С_х = С₀₁ – С₀₂.

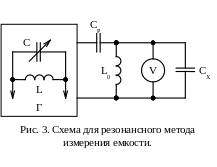
Разновидностью резонансного является генераторный метод измерения. В нём используются два идентичных высокочастотных генератора Г₁ и Г₂ (рис. 4).

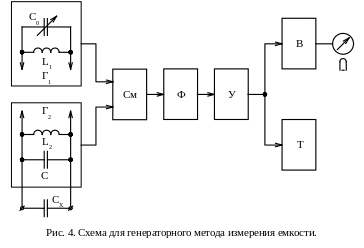
В контур L₁C₀ генератора Г₁ включён опорный конденсатор переменной ёмкости С₀, а параллельно контуру L₂C генератора Г₂ – конденсатор с измеряемой ёмкостью С_х. До подключения С_х генераторы настраивают на одинаковую частоту по нулевым биениям, выделяемым с помощью смесителя См, низкочастотного фильтра Ф, усилителя У и индикатора (телефон Т и магнитоэлектрический прибор, подключённый через выпрямитель В). При подключении конденсатора с измеряемой ёмкостью С_х исчезнувшие нулевые биения восстанавливают изменением ёмкости С₀. Если установить С₀ на условный нуль при начальной настройке, то при втором получении нулевых биений С_х будет равна отсчёту по шкале С₀.

Наиболее точное измерение ёмкости обеспечивает мостовой метод измерения. Применяются уравновешиваемые измерительные мосты переменного тока, в простейшем случае четырёхплечие. В диагональ питания моста подаётся синусоидальное напряжение, а в одно из плеч включён конденсатор с измеряемой ёмкостью С_х (его комплексное сопротивление, соответствующее последовательной или параллельной схемам замещения обозначим Z₁), в трёх других в общем случае – три комплексных сопротивления Z₂, Z₃ и Z₄ (Z₂ и Z₄ – смежные с Z₁, Z₃ – противоположное). Для равновесия моста необходимы два условия: z₁z₃ = z₂z₄ и φ₁ + φ₃ = φ₂ + φ₄, где z₁÷ z₄ – модули Z₁÷ Z₄, φ₁÷ φ₄ – углы сдвига фаз между током и напряжением в сопротивлениях Z₁÷ Z₄. Из этих условий следует, что: а) Z₂÷ Z₄ должны иметь минимум два регулируемых параметра; б) в двух плечах могут быть не комплексные, а чисто активные сопротивления, например, Z₂ = R₂ и Z₃ = R₃, а Z₄ – сопротивление последовательного (рис.5) или параллельного соединения R₄ и С, соответственно для исследуемых конденсаторов с малыми и с большими потерями. Из условий равновесия моста при последовательном соединении R с С_х и R₄ с С легко получить формулу С_х = R₃ С / R₂.

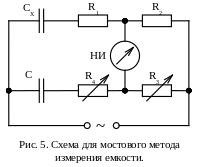
При уравновешивании вручную R₃ и R₄ регулируют поочерёдно, добиваясь каждый раз нового минимального показания нуль-индикатора НИ и приближаясь к нулевому показанию. Высокая чувствительность НИ обеспечивается применением усилителя с выпрямителем и магнитоэлектрическим прибором на выходе. Наиболее высокую точность (погрешность до 0,001 %) обеспечивают трансформаторные мосты с тесной индуктивной связью плеч.

Недостатком мостов, особенно на высоких частотах, является отсутствие общей точки источника питания и НИ. Этот недостаток снят в двойных Т-образных мостах, но они являются частотозависимыми, т.е. при изменении частоты нарушается равновесие. В мостах с автоматическим уравновешиванием и цифровым отсчётом значений С_х (цифровые мосты) применяются разные способы управления регулируемыми элементами по двум каналам. Обычно промышленность выпускает универсальные мосты, позволяющие измерять не только параметры конденсаторов, но и индуктивных катушек, а также сопротивления резисторов. Отечественные приборы, предназначенные для измерения только ёмкости обозначаются Е8, а универсальные – Е7.

{1К20}

Точное решение задачи суммирования погрешностей, т.е нахождение граничного значения Δ_г суммарной погрешности при заданной доверительной вероятности P, возможно лишь в случае, когда известны законы распределения слагаемых (Δ_i). Эти законы практически никогда не известны и их нахождение представляет собой большую самостоятельную задачу.

Если бы законы распределения слагаемых были известны, то задача свелась бы к известной из теории вероятностей задаче о композиции законов распределения, решение которой может быть найдено, например, по методу статистических испытаний.

{1К21}

Согласно [1],

однократное измерение – «измерение, выполненное один раз»;

многократное измерение – «измерение физической величины одного и того же размера, результат которого получен из нескольких следующих друг за другом измерений, т. е. состоящее из ряда однократных измерений»;

наблюдение при измерении – «операции, проводимые при измерении и имеющие целью своевременно и правильно произвести отсчет показаний средства измерений».

Многократные измерения выполняются в случаях, когда результаты однократных измерений флуктуируют, например, из-за помех, причем среднеквадратическое отклонение погрешностей результатов однократных измерений соизмеримо или превышает предел инструментальной погрешности.

За результат многократного измерения после введения поправок обычно принимают среднее арифметическое результатов однократных измерений. Основанием для этого служит тот факт, что среднеквадратическое отклонение погрешности среднего арифметического из n некоррелированных результатов однократных измерений в раз меньше среднеквадратического отклонения погрешности результата однократного измерения. В этом смысле результат многократного измерения точнее результата однократного измерения.

{1К22}

Если ΔX₁, ΔX₂, … ΔX_i, … ΔX_n – погрешности прямых измерений, X_1и, X_2и, … X_iи, … X_nи – истинные значения величин X₁, X₂, … X_i, … X_n, а Y_и и Δ – соответственно истинное значение измеряемой величины Y и погрешность результата косвенного измерения, то

Y_и + Δ = φ(X_1и + ΔX₁, X_2и + ΔX₂, … X_iи + ΔX_i, … X_nи + ΔX_n). (1.43а)

Разложив функцию φ в ряд и ограничиваясь линейным приближением, получим:

Y_и + Δ = φ(X_1и, X_2и, … X_iи, … X_nи) + . (1.43б)

Частные производные необходимо брать в точке истинного значения (X_1и, X_2и, … X_iи, … X_nи), однако практически их можно брать в близкой точке – точке (X₁, X₂, … X_i, … X_n). Учитывая, что Y_и = φ(X_1и, X_2и, … X_iи, … X_nи), из (1.43б) получим:

Δ = . (1.44а)

Слагаемое – составляющая погрешности результата косвенного измерения, вызванная погрешностью ΔX_i результата X_i прямого измерения. Это слагаемое называют частной погрешностью, а приближенную формулу (1.44а) – законом накопления частных погрешностей.

Нетрудно заметить, что формула (1.44а) подобна формуле (1.35), использованная ранее (см. подраздел 1.2.7) при анализе точности средства измерений. Это связано с тем, что математическое описание рассмотренных задач практически одно и то же. При выводе формулы (1.35) речь шла о суммировании частных погрешностей, вызванных отклонением влияющих величин от номинальных значений, а при выводе формулы (1.44а) – о суммировании частных погрешностей, вызванных погрешностями результатов прямых измерений.

ПРИМЕРЫ

{1П1}

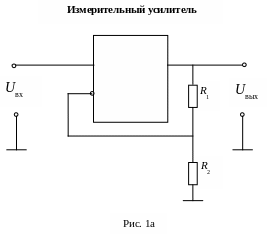
Пример 1. Анализ точности измерительного усилителя.

Измерительный усилитель (ИУ) постоянного напряжения построен на базе операционного усилителя по схеме рис. 1а, где R₁ и R₂ – резисторы отрицательной обратной связи. Диапазон входных напряжений ИУ: ±1 В. Операционный усилитель можно считать идеальным за исключением следующих параметров: ЭДС смещения (Е) и входные токи (I₁ и I₂) не равны нулю.

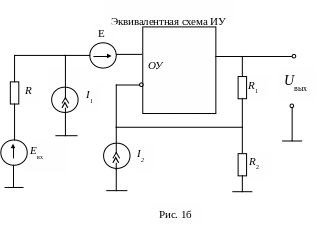
Измерительный усилитель используется для усиления ЭДС Е_вх активного двухполюсника с выходным сопротивлением R. Соответствующая эквивалентная схема представлена на рис. 1б, где ОУ – идеальный операционный усилитель.

Дано:

R_1н = 9 кОм, R_2н = 1 кОм – номинальные значения сопротивлений резисторов R₁ и R₂,

R_1п = R_2п = 0,2 % – предельные значения относительных погрешностей сопротивлений этих резисторов,

I_1п = I_2п = 1 мкА – предельные значения входных токов,

Е_п = 2 мВ – предельное значение модуля ЭДС смещения,

R_п = 1 кОм – предельное значение сопротивления активного двухполюсника.

Необходимо:

Найти предельные значения абсолютной погрешности измерительного усилителя, приведенной ко входу. Построить график зависимости предельных значений погрешностей в функции от U_вх.

Решение.

Прежде всего, найдем функцию Ψ. В данном случае – это зависимость U_вых от U_вх. Для схемы рис. 1б имеем:

. (1)

Из уравнения (1) видно, что влияющими являются величины R₁, R₂, Е и I₂. Величины I₁ и R (выходное сопротивление активного двухполюсника) не влияют на точность измерительного усилителя. Однако эти величины влияют на точность результата измерения Е_вх, так как вызывают погрешность от взаимодействия ИУ и источника Е_вх: Δ_вз = U_вх – Е_вх = I₁R.

Номинальные значения сопротивлений резисторов R₁ и R₂ заданы. Номинальные значения Е_н и I_2н примем равными нулю; при этом ΔE = E – Е_н = E, ΔI₂ = I₂ – I_2н = I₂.

Из (1) можно найти коэффициент усиления ИУ:

.

Номинальный коэффициент усиления ИУ:

Для расчета погрешности ИУ по выходу воспользуемся законом накопления частных погрешностей – формулой (1.35).

В рассматриваемой задаче

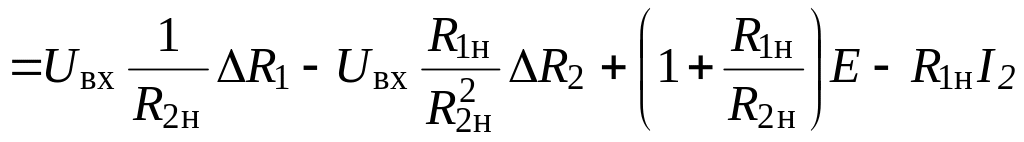. (2)

Из полученного выражения видно, что влияющие величины Е и I₂. вызывают аддитивную составляющую погрешности ИУ, а R₁ и R₂ – мультипликативную.

Найдем ΔR_1п = 0,01·R_1п·R_1п = 18 Ом. Аналогично ΔR_2п = 2 Ом.

Для верхнего предела погрешности ИУ по выходу имеем:

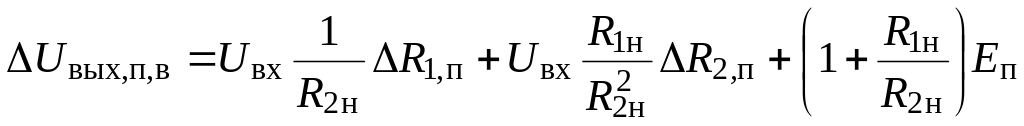= 0,036·U_вх + 0,020.

Для нижнего предела погрешности ИУ по выходу имеем:

=

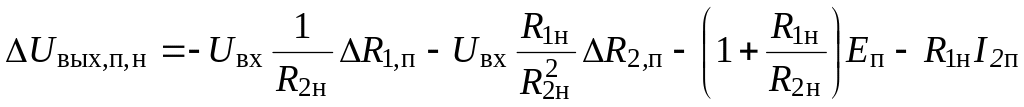= – 0,036·U_вх – 0,029.

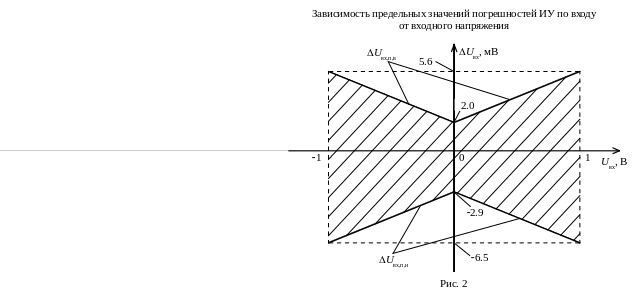
Из полученных выражений видно, что пределы погрешности ИУ по выходу линейно зависят от входного напряжения. При U_вх = 0 ΔU_вых находится в пределах от – 29 до + 20 мВ, а при U_вх = 1 В – в пределах от – 65 до + 56 мВ.

Для определения пределов погрешности ИУ по входу необходимо воспользоваться формулой (1.24). Для рассматриваемой задачи

,

откуда = 3,6·U_вх + 2,0 (мВ), = – 3,6·U_вх – 2,9 (мВ).

Соответствующие графики приведены на рис. 2.

Пример 2. Метрологический расчет измерительного усилителя.

Измерительный усилитель (ИУ) постоянного напряжения построен на базе операционного усилителя по схеме рис. 1а, где R₁ и R₂ – резисторы отрицательной обратной связи. Диапазон входных напряжений ИУ: U_вх = ±1 В. Операционный усилитель можно считать идеальным за исключением следующих параметров: ЭДС смещения (Е) и входные токи (I₁ и I₂) не равны нулю.

Измерительный усилитель используется для усиления ЭДС Е_вх активного двухполюсника с выходным сопротивлением R. Соответствующая эквивалентная схема представлена на рис. 1б, где ОУ – идеальный операционный усилитель.

Дано:

R_1н = 9 кОм, R_2н = 1 кОм – номинальные значения сопротивлений резисторов R₁ и R₂,

0,5/0,2 – класс точности ИУ.

Необходимо:

1. Выбрать

R_1п, R_2п – предельные значения относительных погрешностей резисторов R₁ и R₂,

I_1п , I_2п – предельные значения входных токов ОУ,

Е_п – предельное значение модуля ЭДС смещения ОУ.

2. Доказать, что погрешности ИУ не превышают по модулю предельных значений, гарантируемых классом точности ИУ.

Решение.

Прежде всего, как в примере 1 найдем номинальный коэффициент усиления ИУ (К_н = 10), функцию Ψ зависимости выходного напряжения от входного и влияющих величин (формула (1)) и выражение для погрешности ИУ по выходу (формула (2)).

В примере 1 было установлено, что для данной схемы ИУ наибольшая по модулю погрешность возможна при отрицательных ее значениях. С учетом этого и обеспечивая метрологический запас, получим расчетную формулу для определения пределов влияющих величин:

0,8·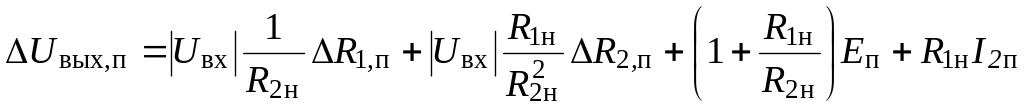 . (3)

Определим теперь ΔU_вых,п – предел погрешности ИУ по выходу.

Так как диапазон входных напряжений ИУ составляет ±1 В, в качестве конечного значения диапазона U_вх,к примем 1 В, тогда конечное значение диапазона выходного напряжения U_вых,к = 10 В (т.к. К_н = 10). Кроме того , ИУ должен иметь класс точности 0,5/0,2. Следовательно, предел его основной абсолютной погрешности (по входу и выходу) может быть найден по формуле (1.32).

Для данного примера

ΔU_вх,п = 0,01·[(0,5 – 0,2)|U_вх| + 0,2 U_вх,к] = 0,003|U_вх| + 0,002; (4)

ΔU_вых,п = К_н·ΔU_вх,п = 0,03|U_вх| + 0,02. (5)

Из полученных выражений видно, что пределы погрешностей ИУ имеют мультипликативную и аддитивную составляющие (соответственно первый и второй члены сумм), причем мультипликативная составляющая зависит согласно (3) от погрешностей резисторов R₁ и R₂, а аддитивная – от влияющих величин Е и I₂. Поэтому формулу (3) можно представить в виде двух выражений:

0,8·0,03·|U_вх| , (6)

0,8·0,02 . (7)

После несложных преобразований получим:

, (6а)

10·Е_п + R_1,н·I_2п = 0,016. (7а)

Из (6а) видно, что на мультипликативную погрешность ИУ относительные погрешности резисторов R₁ и R₂ влияют одинаково. Полагая частные погрешности, вносимые этими резисторами, одинаковыми, получим:

δR_1,п = δR_2,п = 0,024/18 = 0,00133 = 0,133 %,

откуда

ΔR_1п = δR_1,п·R_1н = 0,00133·9000 = 12 Ом,

ΔR_2п = δR_2,п·R_2н = 0,00133·1000 = 1,33 Ом.

Полагая частные погрешности, вносимые влияющими величинами Е и I₂, одинаковыми, из (7а) получим:

Е_п = 0,5·0,1·0,016 = 0,0008 В = 0,8 мВ,

I_2п = 0,5·0,016/R_1н = 0,5·0,016/9000 = 0,89·10^-6 А = 0,89 мкА.

Итак, в результате решения задачи выявлены следующие технические требования к влияющим величинам R₁, R₂, Е и I₂:

δR_1,п = δR_2,п = 0,133 %, Е_п = 0,8 мВ, I_2п = 0,89 мкА.

При этом измерительный усилитель будет соответствовать заданному классу точности 0,5/0,2. Для того, чтобы убедиться в этом, необходимо при ΔU_вых,п , найденных из уравнения (5), проверить, не превышает ли правая часть уравнения (3) левую, для двух значений входного напряжения: U_вх = 0 и U_вх = 1 В.

Практически приходится корректировать технические требования к влияющим величинам, увеличивая пределы одних частных погрешностей за счет уменьшения других. Однако при этом необходимо проверить, соответствует ли ИУ заданному классу точности.

Как уже отмечалось в примере 1, ток I₁ не влияет на погрешность ИУ, но вызывает погрешность от взаимодействия ИУ с источником измеряемого напряжения, пропорциональную значению I₁. Поэтому значение I_1п должно быть по возможности малым. Обычно выбирают I_1п = I_2п.

{1П2}

Пример 3. Обработка прямых измерений.

Необходимо измерить напряжение постоянного тока на выходе активного двухполюсника в режиме холостого хода. Измерение произведено цифровым вольтметром (ЦВ), характеристики которого приведены ниже:

• конечное значение диапазона измерений U_k = 20,00 В;

• цена единицы младшего разряда q = 0,01 В;

• класс точности 0,2/0,1;

• входное сопротивление R = 10 ± 1 Мом;

• нормальная область температур окружающего воздуха 20 ± 5 С;

• рабочая область температур окружающего воздуха от 0 до + 40 С.

Дано:

• показание вольтметра U = 8,43 В;

• температура окружающего воздуха Θ = 35 С;

• выходное сопротивление активного двухполюсника r < 20 кОм.

Требуется:

• Найти искомое напряжение с указанием пределов погрешностей измерения, соответствующих вероятностям P = 1 и P = 0,95;

• записать результат измерения в стандартной форме.

Решение.

Прежде всего, необходимо выяснить: можно ли в качестве результата измерения напряжения холостого хода активного двухполюсника принять показание вольтметра? Напряжение холостого хода U_хх активного двухполюсника равно ЭДС E в его схеме замещения (рис. 1), а вольтметр измеряет напряжение U на своих зажимах. Очевидно, что в общем случае E  U и имеет место погрешность от взаимодействия средства и объекта измерений.

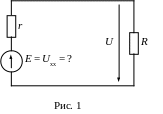
Эта погрешность зависит от структуры и параметров схем замещения средства и объекта измерений. Для данной задачи эти схемы замещения весьма просты: средство измерений (вольтметр) – пассивный двухполюсник с входным сопротивлением R, а объект измерений – активный двухполюсник с выходным сопротивлением r и ЭДС E (рис. 1).

Погрешность от взаимодействия

Δ_вз = U – E = U – U (1 + r/R) = – Ur/R .

Найдем нижнюю (Δ_вз,н) и верхнюю (Δ_вз,в) границы погрешности Δ_вз.

Δ_вз,н = – Ur_max/R_min = – 0,019 В,

Δ_вз,в = – Ur_min/R_max = 0 В.

Поправку η найдем по формуле (1.16):

η = – (Δ_вз,н + Δ_вз,в)/2 = 0,0095 В ≈ 0,01 В.

Теперь по формуле (1.14) найдем исправленное значение результата измерения напряжения холостого хода активного двухполюсника:

U_хх = E = U_испр = U + η = 8,44 В.

Найдем теперь составляющие погрешности полученного результата измерения.

Предел неисключенного остатка погрешности от взаимодействия определим по формуле (1.17). Для рассматриваемой задачи

Δ_вз,п = (Δ_вз,в – Δ_вз,н)/2 = 0,0085 В

Предел основной абсолютной погрешности Δ_о,п цифрового вольтметра определим по формуле (1.32):

Δ_о,п = 0,01[(c – d)|U| + dU_к] = 0,02843 В.

Предел дополнительной абсолютной погрешности Δ_д,п ЦВ, вызванной отклонением температуры окружающего воздуха от нормального значения (20ºC), определим по формуле (1.33):

Δ_д,п = 0,1· Δ_о,п·|Θ – 20| = 0,042645 В.

По условию задачи информация о других дополнительных погрешностях отсутствует. Будем считать, что ими можно пренебречь.

При определении предела абсолютной погрешности результата измерения Δ_п для доверительной вероятности P = 1 воспользуемся формулой (1.39). Для данной задачи

Δ_п = Δ_о,п + Δ_д,п + Δ_вз,п = 0,079575 В ≈ 0,08 В.

Для доверительной вероятности P = 1 результат измерения можно записать в следующем виде:

U_хх = 8,44 ± 0,08 В, P = 1.

При определении граничного значения абсолютной погрешности результата измерения Δ_г для доверительной вероятности P = 0,95 воспользуемся формулой (1.41а). Для данной задачи

В ≈ 0,06 В.

Для доверительной вероятности P = 0,95 результат измерения можно записать в следующем виде:

U_хх = 8,44 ± 0,06 В, P = 0,95.

Пример 4. Обработка прямых измерений.

Необходимо измерить напряжение постоянного тока на выходе активного двухполюсника в режиме холостого хода. Измерение произведено с помощью измерительной установки, состоящей из измерительного усилителя (ИУ), на вход которого подается измеряемое напряжение, и цифрового вольтметра (ЦВ), подключенного к выходу измерительного усилителя.

Технические характеристики измерительного усилителя:

• Диапазон входных напряжений ИУ: ±1 В;

• Номинальный коэффициент усиления K_н = 10;

• Класс точности 0,2;

• Входное сопротивление R_вх – не менее 10 Мом;

• Выходное сопротивление R_вых – не более 1 Ом;

• Входное ток I_вх – не более 0,1 мкА.

• нормальная область температур окружающего воздуха 20 ± 5 С;

• рабочая область температур окружающего воздуха от 0 до + 40 С.

Технические характеристики цифрового вольтметра:

• конечное значение диапазона измерений U_k = 20,00 В;

• цена единицы младшего разряда q = 0,01 В;

• класс точности 0,2/0,1;

• входное сопротивление R = 10 ± 1 Мом;

• нормальная область температур окружающего воздуха 20 ± 5 С;

• рабочая область температур окружающего воздуха от 0 до + 40 С.

Дано:

• показание вольтметра U = 7,93 В;

• температура окружающего воздуха Θ = 32 С;

• выходное сопротивление активного двухполюсника r < 10 кОм.

Требуется:

• Найти искомое напряжение с указанием пределов погрешностей измерения, соответствующих вероятностям P = 1 и P = 0,95;

• записать результат измерения в стандартной форме.

Решение.

Зная напряжение U на выходе ИУ и номинальный коэффициент усиления, найдем напряжение на входе ИУ:

U_вх = U/ K_н = 0,793 В.

Теперь необходимо выяснить, считать ли полученное значение U_вх результатом измерения или его следует исправить?

Для решения этого вопроса нужно оценить погрешности от взаимодействия объекта измерения (активного двухполюсника) с ИУ, а также ИУ с цифровым вольтметром. Оценка погрешности от взаимодействия Δ_вз,1 активного двухполюсника с измерительным усилителем может быть произведена на основе эквивалентной схемы рис. 2.

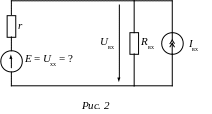
Δ_вз,1 = U_вх – E = – U_вхr/R_вх + I_вх·r·R_вх/(r + R_вх)

Найдем нижнюю (Δ_вз,1,н) и верхнюю (Δ_вз,1,в) границы погрешности Δ_вз,1 считая, что ток I_вх может иметь любое направление, но не превышает по модулю предельного значения I_вх,п = 0,1 мкА, а R_вх/(r + R_вх) ≈ 1 при любых значениях R_вх и r, принадлежащих диапазонам заданных для них значений (R_вх > 10 МОм, r < 10 кОм):

Δ_вз,1,н = – U_вх·r_max/R_вх,min – I_вх,п·r_max = – 0,001793 В.

Δ_вз,1,в = – U_вх·r_min/R_вх,max – I_вх,min·r_min = 0.

Оценка погрешности от взаимодействия Δ_вз,2 измерительного усилителя с цифровым вольтметром может быть произведена на основе эквивалентной схемы рис. 3. Эта погрешность возникает из-за того, что напряжение холостого хода U_вых,хх на выходе ИУ не совпадает с напряжением U , которое измеряется ЦВ.

Для того, чтобы погрешность от взаимодействия ИУ и вольтметра привести ко входу ИУ, ее необходимо разделить на номинальный коэффициент усиления K_н = 10 (см. подраздел 1.2.3). В остальном расчетные формулы не отличаются от формул, использованных в примере 3:

Δ_вз,2 = (U – E)/K_н = – UR_вых/R K_н;

Δ_вз,2,н = – UR_вых,max/R_min K_н ≈ 10^-7 В;

Δ_вз,2,в = – UR_вых,min/R_max K_н = 0.

Рассчитаем теперь нижнюю и верхнюю границы суммарной погрешности Δ_вз = Δ_вз,1 + Δ_вз,2:

Δ_вз,н = Δ_вз,1,н + Δ_вз,2,н = – 0,001793 В;

Δ_вз,в = Δ_вз,1,в + Δ_вз,2,в = 0.

Заметим, что для условий данной задачи погрешность от взаимодействия измерительного усилителя и цифрового вольтметра пренебрежимо мала по сравнению с погрешностью от взаимодействия объекта измерения и измерительного усилителя.

Поправку η найдем по формуле (1.16):

η = – (Δ_вз,н + Δ_вз,в)/2 = 0,0008965 В ≈ 0,0009 В.

Теперь по формуле (1.14) найдем исправленное значение результата измерения напряжения холостого хода активного двухполюсника:

U_хх = U_вх + η = 0,7939 В.

Найдем теперь составляющие погрешности полученного результата измерения.

Предел неисключенного остатка погрешности от взаимодействия определим по формуле (1.17). Для рассматриваемой задачи

Δ_вз,п = (Δ_вз,в – Δ_вз,н)/2 = 0,0008965 В.

Определим составляющие погрешности результата измерения, вносимые погрешностями измерительного усилителя.

Предел основной абсолютной погрешности Δ_о,п,иу ИУ определим по формуле (1.30). Для данной задачи U_вх,н = 1 В – нормирующее значение напряжения на входе ИУ; c = 0,2 – класс точности ИУ.

Тогда

Δ_о,п,иу = 0,01cU_вх,н = 0,002 В.

Предел дополнительной абсолютной погрешности Δ_д,п,иу ИУ, вызванной отклонением температуры окружающего воздуха от нормального значения (20ºC), определим по формуле, приводимой в технической документации на ИУ. Будем считать что там приведена формула (1.33). Тогда

Δ_д,п,иу = 0,1·Δ_о,п,иу·|Θ – 20| = 0,0024 В.

Отметим, что все составляющие погрешности результата измерения, вносимые ИУ приведены к его входу. Погрешности, вносимые цифровым вольтметром, измеряющем напряжение на выходе ИУ, также необходимо привести ко входу усилителя. Для этого необходимо погрешности, вносимые вольтметром, делить на номинальный коэффициент усиления K_н = 10 (см. подраздел 1.2.3).

Предел основной абсолютной погрешности Δ_о,п,цв, вносимой ЦВ и приведенной ко входу ИУ, определим по формуле (1.32) с учетом значения K_н. Для данной задачи U = 7,93 В – напряжение на входе ЦВ, U_к = 20,00 В – конечное значение диапазона измерений ЦВ; c = 0,2 и d = 0,1 определены классом точности вольтметра. Тогда

Δ_о,п,цв = 0,01[(c – d)|U| + dU_к]/K_н = 0,002793 В.

Предел дополнительной абсолютной погрешности Δ_д,п,цв, вносимой ЦВ и приведенной ко входу ИУ, вызванной отклонением температуры окружающего воздуха от нормального значения (20ºC), определим по формуле (1.33) с учетом значения K_н = 10:

Δ_д,п,цв = 0,1·Δ_о,п,цв·| Θ – 20|/K_н = 0,0033516 В.

При определениии предела абсолютной погрешности результата измерения Δ_п для доверительной вероятности P = 1 воспользуемся формулой (1.39). Для данной задачи

Δ_п = Δ_о,п,иу + Δ_о,п,цв + Δ_д,п,иу + Δ_д,п,цв + Δ_вз,п = 0,0105446 В.

Для доверительной вероятности P = 1 результат измерения можно записать в следующем виде:

U_хх = 0,794 ± 0,011 В, P = 1.

При определениии граничного значения абсолютной погрешности результата измерения Δ_г для доверительной вероятности P = 0,95 воспользуемся формулой (1.41а).

Для данной задачи

В.

Для доверительной вероятности P = 0,95 результат измерения можно записать в следующем виде:

U_хх = 0,7939 ± 0,0054 В, P = 0,95.

{1П3}

Пример 5. Обработка косвенных измерений.

Необходимо измерить мощность, потребляемую нагрузкой, если получены следующие результаты прямых измерений: сопротивление нагрузки равно R ± ΔR_п, а ток в нагрузке равен I ± ΔI_п.

Решение.

Как известно, мощность P_н можно определить по формуле

P_н = φ(I, R) = I²R. (1)

Предельное значение Δ_п погрешности результата косвенного измерения мощности для доверительной вероятности P = 1 можно найти по формуле (1.47). Для рассматриваемого примера

Δ_п = 2IRΔI_п + I²ΔR_п. (2)

Для данной функции φ более наглядно выглядит выражение для предела относительной погрешности δ_п косвенного измерения мощности. Для получения этого выражения необходимо левую и правую части равенства (2) разделить на (1). Тогда

δ_п = 2δ_i,п + δ_r,п,

где δ_i,п – предел относительной погрешности измерения тока, а δ_r,п – предел относительной погрешности измерения сопротивления нагрузки.

Пример 6. Обработка косвенных измерений.

Необходимо измерить сопротивление R_x резистора постоянному току с помощью амперметра и вольтметра. Схема измерений представлена на рис. 1.

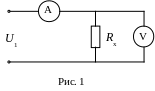
Технические характеристики амперметра:

• конечное значение диапазона измерений I_k = 100 мА;

• количество делений шкалы а_к,а = 100;

• класс точности 1,0;

• входное сопротивление r_a – не более 1 Ом;

• нормальная область температур окружающего воздуха 20 ± 5 С;

• рабочая область температур окружающего воздуха от 0 до + 40 С.

Технические характеристики вольтметра:

• конечное значение диапазона измерений U_k = 3 В;

• количество делений шкалы а_к,в = 150;

• класс точности 0,5;

• входное сопротивление R_v = 2,0 ± 0,2 кОм;

• нормальная область температур окружающего воздуха 20 ± 5 С;

• рабочая область температур окружающего воздуха от 0 до + 40 С.

Дано:

• показание вольтметра а_в = 83,5 дел.;

• показание амперметра а_а = 74,3 дел;

• температура окружающего воздуха Θ = 28 С.

Требуется:

• Найти искомое сопротивление R_x с указанием пределов погрешностей измерения, соответствующих вероятностям P = 1 и P = 0,95;

• записать результат измерения в стандартной форме.

Решение.

По показаниям амперметра (а_а) и вольтметра (а_в) найдем ток (I) и напряжение (U):

I = а_а I_k /а_к,а = 74,3·100/100 = 74,3 мА;

U = а_вU_k /а_к,в = 83,5·3/150 = 1,67 В,

а затем вычислить отношение

U/I = 22,476 Ом.

Теперь необходимо выяснить: принять ли в качестве результата косвенного измерения отношение U/I или внести в него поправку?

Для ответа на этот вопрос рассмотрим эквивалентную схему рис. 2, где E – ЭДС источника напряжения питания, r – его внутреннее сопротивление, r_а – сопротивление амперметра, R_v – сопротивление вольтметра, R_x – искомое сопротивление.

Очевидно, что

U/I = R_x·R_v/(R_x + R_v), (1)

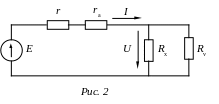
причем это отношение не зависит ни от параметров источника питающего напряжения (E и r), ни от сопротивления амперметра (r_а). Однако U/I ≠ R_x, так как амперметр измеряет ток не через R_x, а через параллельное соединение R_x и R_v. Соответствующая методическая погрешность:

ΔR_x,мет = U/I – R_x. (2)

Из уравнения (1) можно найти выражение для R_x:

(3)

и подставить его в (2).

После преобразований получим:

ΔR_x,мет = . (4)

Полученное выражение позволяет рассчитать поправку и пределы неисключенных остатков систематической методической погрешности по методике, изложенной в подразделе (1.1.3).

Нижняя (ΔR_x,мет,н) и верхняя (ΔR_x,мет,в) границы систематической погрешности:

ΔR_x,мет,н = = – 0,2842 Ом,

ΔR_x,мет,в = = – 0,2320 Ом.

Поправка:

η = – (ΔR_x,мет,н + ΔR_x,мет,в)/2 = 0,2581 Ом.

Исправленный результат косвенного измерения:

R_x = U/I + η = 22,476 + 0,2581 = 22,7341 Ом.

Предел неисключенных остатков методической погрешности:

ΔR_x,мет,п = (ΔR_x,мет,в – ΔR_x,мет,н)/2 = 0,0261 Ом.

Найдем теперь предельные значения составляющих абсолютной погрешности вольтметра – основной (ΔU_о,п), дополнительной (ΔU_д,п) и отсчитывания (ΔU_отс,п).

Если c_в = 0,5 – класс точности вольтметра, а U_к = U_н = 3 В – нормирующее значение, то согласно (1.30)

ΔU_о,п = 0,01c_вU_н = 0,015 В.

Предел дополнительной абсолютной погрешности ΔU_д,п, вызванной отклонением температуры окружающего воздуха (Θ = 28 С) от нормального значения (20ºC), определим по формуле (1.33):

ΔU_д,п = 0,1· ΔU_о,п·|Θ – 20| = 0,012 В.

Предельное значение погрешности отсчитывания для стрелочного прибора обычно принимают равным половине цены деления шкалы. Для используемого в данном эксперименте вольтметра

ΔU_отс,п = 0,5U_k /а_к,в = 0,5·3/150 = 0,01 В.

Предельные значения составляющих абсолютной погрешности амперметра – основной (ΔI_о,п), дополнительной (ΔI_д,п) и отсчитывания (ΔI_отс,п) рассчитываются аналогично:

ΔI_о,п = 0,01c_аI_н = 0,01·1,0·100 = 1 мА;

ΔI_д,п = 0,1· ΔI_о,п·|Θ – 20| = 0, 8 мА;

ΔI_отс,п = 0,5I_k /а_к,а = 0,5·100/100 = 0,5 мА.

Воспользуемся формулой (1.45) и найдем выражение для частных погрешностей – составляющих погрешностей результата косвенного измерения сопротивления, вызванных погрешностями вольтметра:

.

Рассчитаем пределы частных погрешностей, вызванных погрешностями вольтметра.

0,2019 Ом;

0,1615 Ом;

0,1346 Ом.

Воспользуемся формулой (1.45) и найдем выражение для частных погрешностей – составляющих погрешностей результата косвенного измерения сопротивления, вызванных погрешностями амперметра:

.

Рассчитаем пределы частных погрешностей, вызванных погрешностями амперметра.

0,3025 Ом;

0,2420 Ом;

0,1513 Ом.

Предельное значение ΔR_x,п погрешности результата косвенного измерения для доверительной вероятности P = 1 можно найти по формуле (1.47):

ΔR_x,п = ΔR_x,мет,п + ΔR_x,в,о,п + ΔR_x,в,д,п + ΔR_{x,в,отс,п} + ΔR_x,а,о,п + ΔR_x,а,д,п + ΔR_{x,а,отс,п} .

ΔR_x,п = 1,2199 Ом.

Для доверительной вероятности P = 1 результат косвенного измерения можно записать в следующем виде:

R_x = 22,7 ± 1,3 Ом, P = 1.

Граничное значение ΔR_x,г погрешности результата косвенного измерения для доверительной вероятности P = 0,95 можно найти по формуле (1.48). В результате вычислений получим: ΔR_x,г = 0,5598 Ом.

Для доверительной вероятности P = 0,95 результат косвенного измерения можно записать в следующем виде:

R_x = 22,73 ± 0,56 Ом, P = 0,95.

Контрольные работы {1КР1}.