
4. Схемы активных фильтров
Рассмотрим наиболее часто используемую схему активного фильтра – схему Саллена и Кея (УНИН), расчет которой будем осуществлять в данном курсовом проекте.
Схема Саллена и Кея (УНИН)
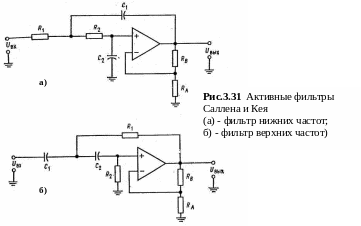
УНИН — это управляемый напряжением источник напряжения. В схемах Салена и Кея операционный усилитель используется как УНИН. Схемы активных фильтров пропускания нижних и верхних частот Салена и Кея второго порядка показаны на рисунке 2.
Эти схемы популярны и недороги, и их легко настраивать. Эти схемы содержат по две RC-цепи , каждая из которых вносит 6 дБ/октава в наклон характеристики на переходном участке. В фильтре пропускания нижних частот цепи R1 C1 и R2 C2 являются интегрирующими, а в фильтре пропускания верхних частот – дифференцирующими. Сопротивления RA, RB определяют коэффициент затухания. затухания. Характеристика вблизи края полосы пропускания формируется за счет обратной связи, которая осуществляётся через конденсатор C1 в случае фильтра пропускания нижних частот или через сопротивление R1 в случае фильтра пропускания верхних частот. Если R1 = R2 и C1 = C2то величины компонент таких фильтров легко рассчитать. Коэффициент усиления фильтров Саллена и Кея должен оставаться постоянным при изменениях RA, и RB , необходимых для установки коэффициента затухания и вместе с ним типа фильтра.
5. Каскадное соединение фильтров
Если нужен фильтр с числом полюсов, большим двух, то его легко можно построить, соединив последовательно несколько фильтров более низкого порядка.
Соединяя каскадно фильтры первого и второго порядков, можно получить фильтр любого более высокого порядка. Каскадное соединение фильтра второго порядка и фильтра первого порядка дает фильтр третьего порядка, а каскадное соединение двух фильтров второго порядка дает фильтр четвертого порядка. Увеличивая число соединяемых фильтров первого и второго порядков, можно получить фильтр любого нужного нам порядка. Фильтры нечетных порядков обычно строятся из фильтра первого порядка в качестве первого каскада и нескольких фильтров второго порядка в качестве остальных каскадов. Фильтры четных порядков строятся из n/2 каскадов второго порядка, где n — желаемый порядок фильтра.
В многокаскадных полосовых фильтрах обычно используется четное число каскадов. Если ширина полосы пропускания полосового фильтра больше чем 50% f0, то такой полосовой фильтр проще построить из фильтра верхних и нижних частот, соединив эти фильтры каскадно. Построенный таким образом полосовой фильтр четвертого порядка будет состоять из двух фильтров верхних частот второго порядка и из двух фильтров нижних частот второго порядка.
