Министерство образования и науки российской федерации

Федеральное государственное бюджетное образовательное учреждение

высшего профессионального образования

Национальный исследовательский томский политехнический университет

Институт неразрушающего контроля

Направление – Приборостроение

Кафедра – Физические методы и приборы контроля качества

Отчет по лабораторной работе №6

«Построение контрольных карт, расчет показателей возможности процесса в программе EXcel».

по курсу «Математическая методы обработки экспериментальных данных»

Выполнил студент гр.1Б01 13.05.2012 Д.В.Струговцов

^{Подпись Дата И.О.Фамилия}

Проверил доцент каф. ФМПК ________ _______ Л.А. Редько

^{должность Подпись Дата И.О.Фамилия}

Томск – 2012 г.

Цель работы: Получить теоретические знания и практические навыки по оценке стабильности процесса, собственной и полной его изменчивости, расчету показателей возможностей процессов и определению ожидаемого уровня несоответствий.

Задачи работы:

- построить контрольные - R карты;

- проанализировать полученные графики;

- рассчитать показатели возможности процесса;

- сделать выводы;

- построить р – карту;

- проанализировать полученный график;

Сделать выводы и заключение по работе.

Основные понятия:

Контрольные карты по количественному/ альтернативному признаку; контрольные границы; выход точки за контрольные границы; процесс в статистически (не)управляемом состоянии; собственная/ полная изменчивость процесса; индексы воспроизводимости (C_p, C_pk) и пригодности (P_p, P_pk) процесса.

Обозначения и сокращения

- объем подгруппы, число выборочных наблюдений в подгруппе;

- число подгрупп;

- измеряемая характеристика качества (индивидуальные значения записываются как ( , , …)). Иногда вместо используют ;

- среднее значение для подгруппы, ;

- среднее средних значений подгрупп;

- истинное среднее процесса;

- медиана подгруппы. Для выборки объема , значения , , которой упорядочены по возрастанию или по убыванию, медиана есть центральное значение, если нечетно, и среднее двух центральных значений, если четно;

- среднее значение медиан подгрупп;

- размах подгруппы (разность наибольшего и наименьшего значений в подгруппе);

Примечание - В случае контрольной карты индивидуальных наблюдений представляет собой скользящий размах, то есть абсолютную разность двух последовательных значений , и т.д.

- среднее значение для всех подгрупп;

- выборочное стандартное (среднее квадратическое) отклонение ;

- среднее выборочных стандартных (средних квадратических) отклонений подгрупп;

- истинное внутригрупповое стандартное отклонение;

- оцененное внутригрупповое стандартное отклонение процесса;

- число несоответствующих единиц в подгруппе;

- доля несоответствующих единиц в подгруппе

;

- среднее значение доли несоответствующих единиц

;

- число несоответствий в подгруппе;

- среднее значений для всех подгрупп;

- число несоответствий на единицу в подгруппе;

- среднее значение

;

- центральная линия;

- верхняя контрольная граница;

- нижняя контрольная граница.

- индекс воспроизводимости процесса, оценивающий возможности удовлетворять технический допуск без учета положения среднего значения и применяемый для стабильных по разбросу процессов;

- индекс воспроизводимости процесса, оценивающий возможности удовлетворять технический допуск с учетом фактического положения среднего значения и применяемый для стабильных и по разбросу и по настройке процессов;

- индекс пригодности процесса удовлетворять технический допуск без учета положения среднего значения, применяемый для процессов, стабильность которых по разбросу не подтверждена;

- индекс пригодности процесса удовлетворять технический допуск с учетом положения среднего значения, применяемый для процессов, стабильность которых по разбросу не подтверждена;

- коэффициент воспроизводимости процесса, стабильность которого подтверждена;

- коэффициент пригодности процесса, стабильность которого не подтверждена;

- число несоответствующих единиц на миллион единиц продукции;

Краткая теория

Любые измерения в контрольных точках или на выходе технологического процесса (ТП) могут осуществляться по количественному или альтернативному признакам.

При получении данных по количественному признаку контролируемые изделия измеряют по данному показателю качества шкальным прибором или инструментом, позволяющим измерить данный показатель для любого контролируемого изделия в соответствующих единицах, например, диаметр (или его отклонения от заданной величины) в миллиметрах с десятыми (сотыми, тысячными) долями или твердость поверхности изделия после термообработки в единицах Роквелла и т.п.

Все отклонения показателя качества могут быть условно разделены на 2 класса: случайные и неслучайные.

Случайные отклонения являются итогом действия многих относительно несущественных дестабилизирующих причин, присутствующих при нормальном ходе ТП. Такие причины называют обычными.

Неслучайные отклонения являются итогом действия значительных дестабилизирующих причин, которые существенно изменяют ход ТП, например, переналадка станка, новая партия заготовок или отдельные заготовки в партии с другой твердостью и т.п. Такие причины изначально могут быть неизвестны, но они должны быть обнаружены и изучены по мере наблюдения и анализа работы ТП. Такие причины называют особыми.

Если на ТП действуют только обычные причины (факторы), колебания показателя качества в контрольных точках ТП будут сравнительно небольшими и достаточно устойчивого характера. При этом говорят, что процесс находится в статистически устойчивом, или управляемом, состоянии.

Если же на ТП воздействуют особые (неслучайные) причины, то они выводят ТП из статистически устойчивого состояния, при этом контролируемый показатель качества значительно изменяет свое среднее значение или значительно увеличивается разброс, что не может произойти по случайным при-чинам. Такое отклонение считается сигналом проявления особой причины.

Для того, чтобы различать эти два вида причин, существует такой инструмент, как контрольные карты. Контрольная карта - это графическое средство, использующее статистические подходы, важность которых для управления производственными процессами была впервые показана доктором У.Шухартом в 1924 г.

Т.о. цель контрольных карт - обнаружить неестественные изменения в данных из повторяющихся процессов и дать критерии для обнаружения отсутствия статистической управляемости. Процесс находится в статистически управляемом состоянии, если изменчивость вызвана только случайными причинами. При определении этого приемлемого уровня изменчивости любое отклонение от него считают результатом действия особых причин, которые следует выявить, исключить или ослабить.

Карта Шухарта требует данных, получаемых выборочно из процесса через примерно равные интервалы. Интервалы могут быть заданы либо по времени (например ежечасно), либо по количеству продукции (каждая партия). Обычно каждая подгруппа состоит из однотипных единиц продукции или услуг с одними и теми же контролируемыми показателями, и все подгруппы имеют равные объемы. Для каждой подгруппы определяют одну или несколько характеристик, таких как среднее арифметическое подгруппы и размах подгруппы или выборочное стандартное отклонение . Карта Шухарта - это график значений определенных характеристик подгрупп в зависимости от их номеров. Она имеет центральную линию ( ), соответствующую эталонному значению характеристики. При оценке того, находится ли процесс в статистически управляемом состоянии, эталонным обычно служит среднее арифметическое рассматриваемых данных. При управлении процессом эталонным служит долговременное значение характеристики, установленное в технических условиях, или ее номинальное значение, основанное на предыдущей информации о процессе, или намеченное целевое значение характеристики продукции или услуги. Карта Шухарта имеет две статистические определяемые контрольные границы относительно центральной линии, которые называются верхней контрольной границей ( ) и нижней контрольной границей ( ) (рисунок 1).

Контрольные границы на карте Шухарта находятся на расстоянии 3 от центральной линии, где - генеральное стандартное отклонение используемой статистики. Изменчивость внутри подгрупп является мерой случайных вариаций.

Существуют следующие контрольные карты (КК) для количественных данных:

1) карты среднего ( X ) и размахов (R) или выборочных стандартных отклонений (S);

2) карта индивидуальных значений (X) и скользящих размахов (R);

3) карта медиан (M) и размахов (R);

Примечание. Правила построения, расчет контрольных границ, методы управления и интерпрета-ции КК для количественных данных см. в ГОСТ Р 50779.42–99 «Статистические методы. Контрольные карты Шухарта», п. 5 – 8.

Таблица 1. Формулы для контрольных границ карт Шухарта для количественных данных

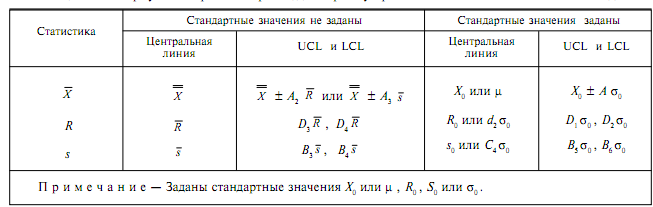
Таблица 2. Коэффициенты для вычисления линий контрольных карт:

Проверка структур на особые причины

Существует 8 критериев по которым можно судить о действии на процесс особых, неслучайных причин (рисунок 2).

Этот набор критериев можно принять за основу, но пользователи контрольных карт должны обращать внимание на любую необычную структуру точек, которая может указывать на проявление особых (неслучайных) причин.

Поэтому эти критерии следует рассматривать только как примеры ситуаций, когда может быть установлено проявление неслучайных причин.

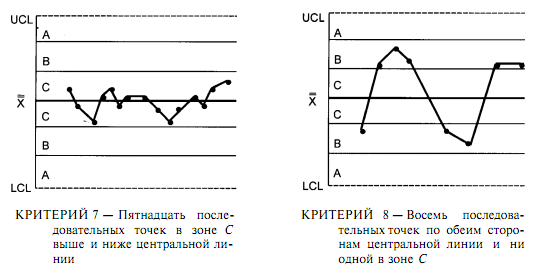
Рисунок 2. Критерии для определения особых причин

Контрольные карты для альтернативных данных

Альтернативные данные представляют собой наблюдения, фиксирующие наличие или отсутствие некоторых характеристик (или признаков) у каждой единицы рассматриваемой подгруппы. На основе этих данных производится подсчет числа единиц, обладающих или не обладающих данным признаком, или числа таких событий в единице продукции, группе или области. Альтернативные данные в общем случае могут быть получены быстро и дешево, для сбора их не требуется специального обучения.

Контрольные карты для данных по альтернативному признаку подразделяют на четыре вида:

р-карта – для контроля доли несоответствующих (дефектных) изделий в выборке;

nр-карта – для контроля числа несоответствующих (дефектных) изделий в выборке заданного объема n;

с-карта – для контроля числа несоответствий (дефектов) в единице продукции;

u-карта – для контроля среднего числа несоответствий (дефектов) в расчете на одно изделие в выборке или на единицу площади, объема, веса и т.п. для нештучной продукции.

Таблица 3. Формулы для контрольных границ карт Шухарта для альтернативных данных

Различают два типа перечисленных видов контрольных карт.

1-й тип предполагает, что для контролируемой величины не задано стандартное значение, и его значение определяют экспериментально на этапе предварительного исследования, который проводится в естественных производственных условиях при нормальном ходе ТП. Тогда на этапе предварительного исследования следует получить выборочное среднее значение (для соответствующих карт):

р – средняя доля несоответствующих изделий для выпускаемой продукции (для р- и nр-карт);

с – среднее число несоответствий в единице продукции (для с-карт);

u – среднее число несоответствии в расчете на одно изделие в выборке или на единицу площади, объема, веса и т.п. для нештучной продукции (для u-карт).

2-й тип предполагает, что стандартное значение, соответственно р0, с0 или u0, задано как норматив.

Показатели возможностей процесса

Показатели возможностей характеризуют потенциальные и фактические возможности процесса удовлетворять установленным техническим допускам для значений выходного показателя качества, измеряемого по количественному признаку.

Для применения показателей возможностей должны быть выполнены следующие условия:

• индивидуальные значения показателей качества отдельных единиц продукции должны подчиняться нормальному закону распределения или близкому к нему;

• предварительно должна быть проведена оценка стабильности процесса;

• изменчивость результатов измерений, обусловленная измерительной системой, а не только погрешностью измерительных приборов, должна быть мала по сравнению с техническим допуском.

Показатели, применяемые для оценки возможностей стабильного процесса, называют индексами воспроизводимости процесса Ср и Cpk.

Показатели, применяемые для оценки возможностей процессов, стабильность которых не подтверждена, называют индексами пригодности процесса Рр и Ppk.

Потенциальные возможности процессов в предположении, что среднее процесса настроено или может быть настроено на центр поля допуска, оценивают с помощью индексов Ср и (или) Рр.

Если среднее процесса отлично или может быть отлично от центра поля допуска, то дополнительно для анализа процессов следует применять индексы Cpk и (или) Ppk.

Индексы воспроизводимости стабильных процессов позволяют сделать оценку и (или) прогноз уровня несоответствий продукции на выходе процесса.

Оценка собственной и полной изменчивости процесса

Собственную и полную изменчивость (вариабельность) процесса следует оценивать по данным, которые были использованы для построения контрольных карт Шухарта. Собственная изменчивость процесса зависит от влияния только обычных (общих) причин вариаций, ее следует определять для стабильных по разбросу процессов.

Собственную изменчивость стабильного по разбросу процесса следует оценивать выборочным стандартным отклонением .

- при использовании Х- и MR-карт Шухарта

, (1)

где - среднее значение скользящих размахов;

- коэффициент, значения которого зависят от числа точек, использованных для расчета скользящих размахов в MR-карте;

- при использовании - и R-карт Шухарта

, (2)

где - среднее значение размахов отдельных выборок;

- коэффициент, значения которого зависят от объема отдельных выборок в R-карте;

- при использовании - и S-карт Шухарта

, (3)

где - среднее значение стандартных отклонений отдельных выборок;

- коэффициент, значения которого зависят от объема отдельных выборок в S-карте.

Таблица 4. Значения коэффициентов и

2	1,128	0,7979
3	1,693	0,8862
4	2,059	0,9213
5	2,326	0,9400

Полная изменчивость процесса зависит от влияния как случайных (обычных), так и неслучайных (особых) причин вариаций.

Полную изменчивость процесса следует оценивать выборочным стандартным отклонением по формуле

, (4)

где - суммарный объем данных во всех выборках объема каждая (в объединенной выборке );

- результат измерений показателей качества отдельных единиц продукции, =1, ..., ;

- среднее арифметическое всех значений в объединенной выборке

. (5)

Расчет показателей возможностей процессов

Если целевое значение параметра не указано, то значения , , и следует рассчитывать по формулам:

; (6)

; (7)

; (8)

, (9)

где и - соответственно наибольшее и наименьшее предельные значения показателя качества (пределы поля допуска).

В некоторых случаях по усмотрению пользователя настоящего стандарта или по требованию потребителя могут быть применены иные показатели возможностей процесса, например коэффициент воспроизводимости стабильного процесса

(10)

и коэффициент пригодности процесса, стабильность которого не подтверждена

. (11)

В ряде случаев может быть установлен только один предел поля допуска: либо наибольшее предельное значение , либо наименьшее предельное значение показателя качества. Тогда для оценки возможностей процесса применяют только индексы и , которые рассчитывают по следующим формулам:

- для стабильного процесса в состоянии А, если задано наибольшее предельное значение показателя качества , то

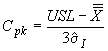, (12)

если задано наименьшее предельное значение показателя качества , то

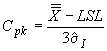, (13)

- для нестабильного процесса в состояниях Б и В, если задано наибольшее предельное значение показателя качества , то

, (14)

если задано наименьшее предельное значение показателя качества , то

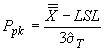. (15)

В случаях, когда одно из предельных значений существует в виде естественного физического предела значений контролируемого признака, обычно устанавливают только одно предельное значение (наибольшее или наименьшее).

Тогда для оценки возможностей процесса применяют только индексы и по формулам (12)-(15) соответственно.

Примечание - Примерами могут служить следующие требования: биение торца - не более 5 мкм (физический предел равен 0 мкм); концентрация нежелательного вещества - не более 0,1% (физический предел 0%); концентрация желательного компонента - не менее 99,5% (физический предел 100%).

Если индивидуальные значения (результаты измерения отдельных единиц продукции) подчиняются нормальному распределению, то для стабильного процесса можно оценить ожидаемый уровень несоответствий. Значение ожидаемого уровня несоответствий в этом случае равно половине значения (в процентах несоответствующих единиц продукции или ), указанного в таблице для полученного по формуле (12) или (13) значения .