Продолжение таблицы 3
Номер варианта |
Исходная система |
Номер варианта |
Исходная система |
5 |
,
,
,
|
20 |
,
|
6 |
, , , |
21 |
, , , |
7 |
, , , |
22 |
,
,
,
|
8 |
, , , |
23 |
, , , |
9 |
,
,
|
24 |
, , , |
10 |
, , , |
25 |
, , , |
11 |
,
,
,
|
26 |
, , , |
12 |
, , , |
27 |
, , , |
13 |
, , , |
28 |
, , , |
14 |
, , , |
29 |
, , , |
15 |
, , , |
30 |
, , , |
,
,
,
1.7 Определение минимума функционала градиентным методом
Цель работы: используя градиентный метод, определить минимум функционала:
z(x,y)=a1x2+a2y2+a3xy+a4x+a5y+a6.
Рекомендация к выполнению задания
Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т.д.).
Входные параметры программы:
a1, …, a6 – числовые коэффициенты функционала;
– погрешность;
– длина шага спуска;
(x(0), y(0)) – начальное приближение.
Выходные параметры программы:
t – число итераций;
(x(t),
y(t))
–
приближенное решение на итерации
;
z(x(t), y(t)) – значение функции в точке приближенного решения;
|grad z(x(t), y(t))| – значение градиента функции на итерации.
Примечание –
ввести выбор
задания длины шага
.
1 способ: – const.
2 способ: расчет для каждого шага t.
Отчет по самостоятельной работе должен содержать:
постановку задачи;
блок-схему реализации вычисления минимума параболоида вращения;
программу решения задачи.
Теоретические сведения
Задача определения минимума функционала градиентным методом эквивалентна задаче нахождения решения системы нелинейных уравнений. Рассмотрим двумерный случай. Пусть система уравнений имеет вид:
(14)
Введем новую функцию вида:
Ф(x,y)=f 2(x,y)+g2(x,y).
Т. к. функция Ф(x,y) неотрицательна, то найдется точка (x*,y*) такая, что:
Ф(x,y)
Ф(x*,y*)
(x,y)R2.
Ели удаётся определить точку (x*,y*), минимизирующую функцию Ф(x,y), и если minФ(x,y) = Ф(x*,y*), значит (x*,y*) – искомое решение системы (14).
Итерационная последовательность будет иметь следующий вид:
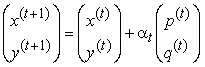, (15)
где t = 0, 1, 2, 3, …;
–
вектор, определяющий
направление минимизации;
t – скаляр (шаговый множитель), характеризующий длину шага.
Вектор минимизации выбирается как антиградиент функции Ф(x,y):
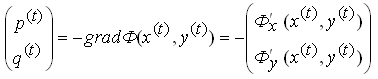. (16)
Длина шага может быть постоянной на каждом итерационном шаге либо для каждого шага рассчитываться по формуле:
t =arg minФ(x(t)-Фx(x(t),y(t)), y(t)-Фy(x(t),y(t))). (17)
При минимизации функции Ф(x,y) следует определиться:
– как выбирать направление спуска;
– как регулировать длину шага в выбранном направлении с помощью скалярного параметра.
Если подобрать множитель так, что Ф(Xk+pk,Yk+qk)<Ф(Xk,Yk),
где Xk+1=Xk+pk, Yk+1=Yk+qk, это будет означать переход на каждой итерации в точку с меньшим значением минимизирующей функции.
1.8 Определение минимума функционала методом сопряженных градиентов
Цель работы: используя метод сопряженных градиентов, определить минимум функционала.
Рекомендация к выполнению задания
Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т. д.).
Входные параметры программы:
n – размерность системы
a11, …, ann – числовые коэффициенты исходной системы;
– погрешность;
(x(0), y(0)) – начальное приближение.
Выходные параметры программы:
– число итераций;
(x(t), y(t)) – приближенное решение на итерации ;
z(x(t), y(t)) – значение функции в точке приближенного решения;
rt(x(t), y(t)) – невязка на каждом шаге;
(x(*), y(*)) – точка минимума функционала или решение СЛАУ.
Отчет по самостоятельной работе должен содержать:
постановку задачи;
блок-схему реализации вычисления минимума функционала;
программу решения задачи.
Теоретические сведения
Задачу определения минимума функционала методом сопряженных градиентов можно рассматривать как задачу о решении системы линейных алгебраических уравнений. Рассмотрим общий случай.
Пусть
–
нормальная n-мерная
система линейных алгебраических
уравнений, где А
–
симметричная и положительно определенная
матрица.
Образуем квадратичный функционал вида:
Ф(X)=(AX,X)-2(B,X)+C, (18)
где CR1 - const;
(*,*) – скалярное произведение в пространстве Rn.
Задача решения нормальной системы и задача минимизации функционала (18) эквивалентны.
Пусть X* - точное решение системы , тогда:
Ф(X*)=
Ф(X). (19)
Рассмотрим метод сопряженных градиентов. Введем следующие обозначения:
X(0), …, X(k) – приближения к точному решению X*;
r(0), …, r(k) – невязки на каждом шаге, играющие роль антиградиента функции Ф(X);
p(k) – направление минимизации функционала Ф(X) в точке X(k);
k – коэффициент, обеспечивающий минимум Ф(X) в направлении p(k);
k – коэффициент при p(k) в формуле для вычисления p(k+1),
обеспечивающий А – сопряженность векторов p(k) и p(k+1) (т. е. p(k) ортогональны всем предыдущим невязкам r(k-1));
q(k) – вспомогательный вектор.
Алгоритм метода сопряженных градиентов
Шаг 1.
Задаём X(0) – начальное приближение;
>0 – погрешность решения;
r(0)=B-AX(0) – невязка на начальном приближении;
p(0)= r(0) – направление минимизации на нулевом шаге.
Шаг 2.
Вычисляем вектор q(k)=Ap(k), k – номер итерации;
вычисляем пошаговый
множитель
;
вычисляем следующее приближение X(k+1)=X(k)+kp(k);
вычисляем невязку на шаге (k+1): r(k+1)=r(k)+kq(k).
Шаг 3.
Если ||r(k+1)||, то итерационный процесс останавливается и выводится решение X(k+1);
иначе
вычисляем скаляр
;
вычисляем новое направление минимизации вектор
p(k+1)=r(k+1)-kp(k);
полагаем k=k+1, переходим к Шагу 2.
2. ЧИСЛЕННЫЕ МЕТОДЫ РЕШЕНИЯ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ
2.1 Метод Пикара
Цель работы: методом последовательных приближений найти приближенное решение дифференциального уравнения:
y = f(x). (20)
Отчет по самостоятельной работе должен содержать:
постановку задачи;
расчеты по вычислению приближенных функций с учетом начального условия;
оценку погрешности k-го приближения в области G: |x-x0| а, |y-y0| b.
Теоретические сведения
Итерационная формула метода Пикара при n=1, 2, … имеет вид:
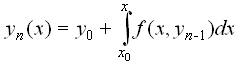. (21)
Оценка погрешности k-го приближения задаётся формулой:
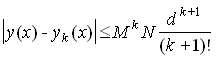, (22)
где
M=max|fy(x,y)| – константа Липшица,
N– верхняя грань модуля функции f: |f(x,y)|N,
величина d
для определения окрестности |x-x0|d,
вычисляемая по формуле: d=min(a,
).
ПРИМЕР. Методом последовательных приближений найти приближенное решение дифференциального уравнения
y =x3-2y, удовлетворяющее начальному условию y(0)=1.
Запишем для нашего уравнения итерационную формулу вида (21):
.
Выберем за начальное приближение y0=y(0)=1. Имеем:
.
Продолжая итерационный процесс, далее получаем:
;
и т. д.
Оценим погрешность третьего приближения. Для этого определим область G, в которой функция f(x,y) определена, непрерывна и удовлетворяет условию Липшица. Зададим область G в виде неравенств:
|x-x0| а, |y-y0| b.
Зададим, для примера, а = 1 и b = 3. В прямоугольнике |x-0|1,
|y-1|3 функция f(x,y)=x3-2y определена и непрерывна, причем:
M=max|fy(x,y)|=2, N=max|f(x,y)|= 9.
Из формулы d=min(a,
)
определяем d=
.
По формуле (22) оценка погрешности третьего
приближения равна:
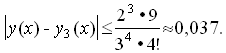
Исходные данные для лабораторной работы выбираются из таблицы 4.
Таблица 4 – Варианты лабораторной работы № 2.1
Номер варианта |
f(x) |
x0 |
y0 |
k (номер последней итерации) |
а |
b |
1 |
|
0 |
3 |
4 |
4 |
5 |
2 |
|
1 |
2 |
5 |
3 |
2 |
3 |
|
2 |
3 |
3 |
1 |
1 |
4 |
|
1 |
0 |
4 |
3 |
5 |
5 |
|
0 |
1 |
5 |
1 |
4 |
6 |
|
2 |
1 |
3 |
1 |
0,5 |
7 |
|
0 |
2 |
3 |
1 |
1 |
8 |
|
1 |
1 |
3 |
1 |
1 |
9 |
|
2 |
0 |
4 |
3 |
2 |
10 |
|
0 |
0 |
3 |
1 |
1 |
11 |
|
2 |
1 |
5 |
1,5 |
0,5 |
12 |
|
2 |
2 |
4 |
1 |
1 |
13 |
|
0 |
1 |
4 |
1 |
1 |
14 |
|
1 |
0 |
3 |
2 |
2 |
15 |
|
3 |
2 |
4 |
3 |
4 |
16 |
|
0 |
1 |
5 |
4 |
3 |
17 |
|
1 |
1 |
3 |
2 |
2 |
18 |
|
2 |
1 |
5 |
3 |
2 |
19 |
|
0 |
1 |
3 |
0,5 |
2 |
20 |
|
1 |
0 |
4 |
1,5 |
3 |
21 |
|
2 |
2 |
3 |
1 |
1 |
