Метод простых итераций

Преобразуем исходную систему (4) к виду

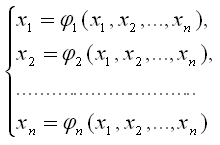
или в векторном виде X=Ф(X).

Итерационная последовательность будет иметь вид:

X^(t+1) = Ф(X^(t+1)), t=0, 1, 2, … . (5)

Итерационная последовательность (5) определяет метод простых итераций (МПИ) или метод последовательных приближений. Процесс построения итерационной последовательности (5) начинается с начального приближения X⁽⁰⁾=( , , …, )^T и продолжается по формуле (5). При определенных условиях эта последовательность со скоростью геометрической прогрессии будет приближаться к вектору – неподвижной точке отображения Ф(X), т. е. решению системы (4).

Алгоритм метода простых итераций

Шаг 1.

Задаем вектор функцию Ф(X);

задаем начальное приближение X⁽⁰⁾=( , , …, )^T;

задаем погрешность  .

Шаг 2.

Вычисляем следующее приближение X^(t+1) = Ф(X^(t+1)) с учетом параллельного итерирования

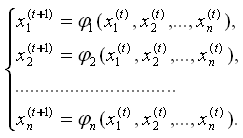
Шаг 3.

Если max|| X_i^(t+1)-X_i^(t)||, то итерационный процесс завершен и решение X^* X^(t+1). Иначе t=t+1, и переходим на шаг 2.

Метод покоординатных итераций

Перепишем итерационную последовательность (5) в развернутом виде:

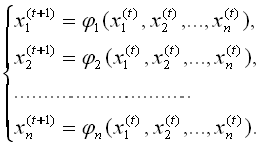(6)

Последовательность (6) напоминает МПИ для СЛАУ при условии, что _i – линейные функции вещественных переменных x₁, x₂, …, x_n. Систему (6) можно модифицировать аналогично методу Зейделя:

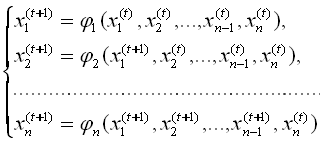. (7)

Алгоритм метода покоординатных итераций

Шаг 1.

Задаем вектор-функцию Ф(X) ;

задаем начальное приближение X⁽⁰⁾=( , , …, )^T ;

задаем погрешность  .

Шаг 2.

Вычисляем следующее приближение X^(t+1) = Ф(X^(t+1)) с учетом последовательного итерирования:

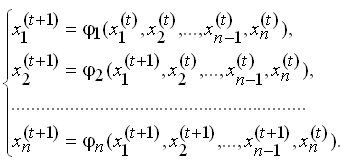
Шаг 3.

Если max|| X_i^(t+1)-X_i^(t)||, то итерационный процесс завершен, и решение X^* X^(t+1) . Иначе t=t+1, и переходим на шаг 2.

Замечание. Отдельные уравнения в системе (7) неравноправны, т.е. перестановка уравнений может изменить в каких-то пределах число итераций и ситуацию со сходимостью итерационного процесса.

Исходная система для выполнения лабораторной работы выбирается согласно таблице 2.

Таблица 2 – Варианты лабораторной работы № 1.3

Номер варианта	Исходная система	Номер варианта	Исходная система
1		16
2		17
3		18

Продолжение таблицы 2

Номер варианта	Исходная система	Номер варианта	Исходная система
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28

Продолжение таблицы 2

Номер варианта	Исходная система	Номер варианта	Исходная система
14		29
15		30

1.4 Решение системы нелинейных уравнений методом Ньютона

Цель работы: используя метод Ньютона, найти решение системы нелинейных уравнений

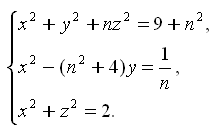
За число n принять номер своего варианта.

Рекомендация к выполнению задания

Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т.д.).

Входные параметры программы:

X⁽⁰⁾ – ненулевое приближение,

 – погрешность.

Выходные параметры программы:

t – число итераций;

X^* – решение системы нелинейных уравнений.

Примечания:

ввести выбор расчета частных производных функций аналитическим и численным методами;

самостоятельно выяснить, при каком начальном приближении система не может быть решена. Чем можно объяснить причину этого явления.

Отчет по самостоятельной работе должен содержать:

постановку задачи;

блок-схему реализации вычисления решения системы нелинейных уравнений;

программу решения задачи.

Теоретические сведения

Для решения системы нелинейных уравнений (4) запишем метод Ньютона в неявном виде:

F(X^(t))[X^(t+1)-X^(t)]=-F(X^(t)), (8)

где - матрица Якоби.

Обозначим за p^(t)=X^(t+1)-X^(t), тогда (8) можно переписать в виде

F(X^(t))p^(t)=-F(X^(t)). (9)

Алгоритм метода Ньютона

Шаг 1.

Задаем вектор-функцию F(X);

Задаем начальное приближение X⁽⁰⁾=( , , …, )^T;

задаем погрешность  .

Шаг 2.

Решаем систему линейных алгебраических уравнений относительно поправки p^(t):

F(X^(t))p^(t)=-F(X^(t)) .

Вычисляем следующее приближение

X^(t+1)=p^(t)+X^(t).

Шаг 3.

Если max|| X_i^(t+1)-X_i^(t)||, то итерационный процесс завершен, и решение X^* X^(t+1). Иначе t=t+1, и переходим на шаг 2.

Замечание. При численном решении методом Ньютона можно заменить производные в матрице Якоби их приближенными конечно-разностными значениями .

1.5 Определение экстремумов функции одной переменной

Цель работы: используя метод золотого сечения и метод парабол, найти минимум функции вида

z(x)=a₁xⁿ+ a₂x^n-1+…+a₀.

Рекомендация к выполнению задания

Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т. д.).

Входные параметры программы:

a₀, …, a_n – числовые коэффициенты исходного уравнения;

 – погрешность;

n – степень многочлена функции;

(A,B) – начальный интервал.

Выходные параметры программы:

t – число итераций;

X^* – точка минимума функции;

z(X^*) – значение функции в точке минимума.

Примечание – учесть возможность сравнения результатов расчета по методу золотого сечения и методу парабол.

Отчет по самостоятельной работе должен содержать:

постановку задачи;

блок-схему реализации вычисления минимума функции одной переменной;

программу решения задачи.

Теоретические сведения

Пусть имеется некоторое множество X, состоящее из элементов , принадлежащих какому-либо метрическому пространству, и на нём определена скалярная функция f(x). Функция f(x) имеет локальный минимум в точке , если существует некоторая окрестность  этой точки, в которой выполняется условие

f( )<f(x), || x- ||<. (10)

У функции может быть много локальных минимумов. Если выполняется условие:

f( )= f(x), (11)

функция достигает абсолютного минимума на данном множестве X.

Необходимое условие: f(x) непрерывна или кусочно-непрерывна на множестве X, а X – компактно и замкнуто.

Пусть X – числовая ось, тогда задачи (10) и (11) – задачи по определению минимума функции одной переменной.