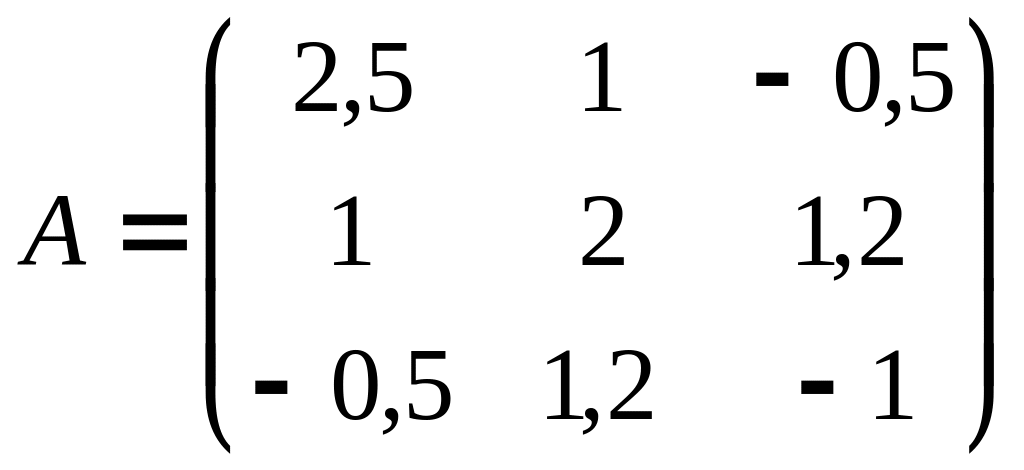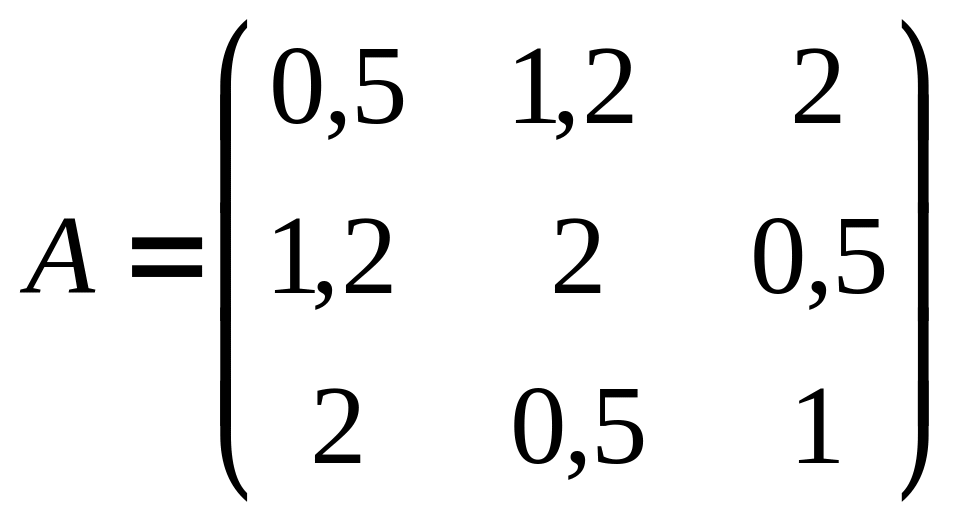Остановка итерационного процесса

Для остановки итерационного процесса можно выбрать следующие варианты:

1. Отношение суммы квадратов внедиагональных элементов к сумме квадратов диагональных элементов должно не превышать наперед заданной погрешности:

,

где  – заданная погрешность.

2. Сумма квадратов внедиагональных элементов должна не превышать наперед заданной погрешности:

.

Таблица 1 – Варианты лабораторной работы № 1.2

Номер варианта	Исходная матрица	Номер варианта	Исходная матрица
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25

Продолжение таблицы 1

Номер варианта	Исходная матрица	Номер варианта	Исходная матрица
11		26
12		27
13		28
14		29
15		30

1.3 Решение систем нелинейных уравнений методами простых итераций и покоординатной итерации

Цель работы: используя метод простых итераций и покоординатных итераций, найти решение системы нелинейных уравнений с точностью до .

Рекомендация к выполнению задания

Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т.д.).

Примечания:

ввести выбор расчета частных производных функций аналитическим и численным методами;

проверить условие сходимости методов в окрестности нулевого приближения;

самостоятельно выяснить, при каком начальном приближении система не может быть решена. Чем можно объяснить причину этого явления.

Входные параметры программы:

X⁽⁰⁾ – ненулевое приближение,

 – погрешность.

Выходные параметры программы:

t – число итераций;

X^* – решение системы нелинейных уравнений.

Отчет по самостоятельной работе должен содержать:

постановку задачи;

блок-схему реализации вычисления решения системы нелинейных уравнений с учетом применения двух итерационных методов;

программу решения задачи.

Теоретические сведения

Пусть задана система нелинейных уравнений с вещественными переменными:

F(X)=0, (4)

где , , , при этом f₁, f₂,…, f_n – заданные нелинейные вещественные функции, определенные и непрерывные в некотором замкнутом множестве .

Необходимо найти такой вектор X^*=( , …, )^T, который при подстановке в систему (4) обращал бы каждое уравнение в верное равенство.

Поставленную задачу можно рассматривать как задачу о нулях нелинейного отображения

F: R_n R_n.

При решении систем нелинейных уравнений F(X)=0 возникают две задачи:

задача отделения корней, т. е. определение областей, в которых лежит по одному решению;

задача уточнения корней, определение корней с заданной точностью.