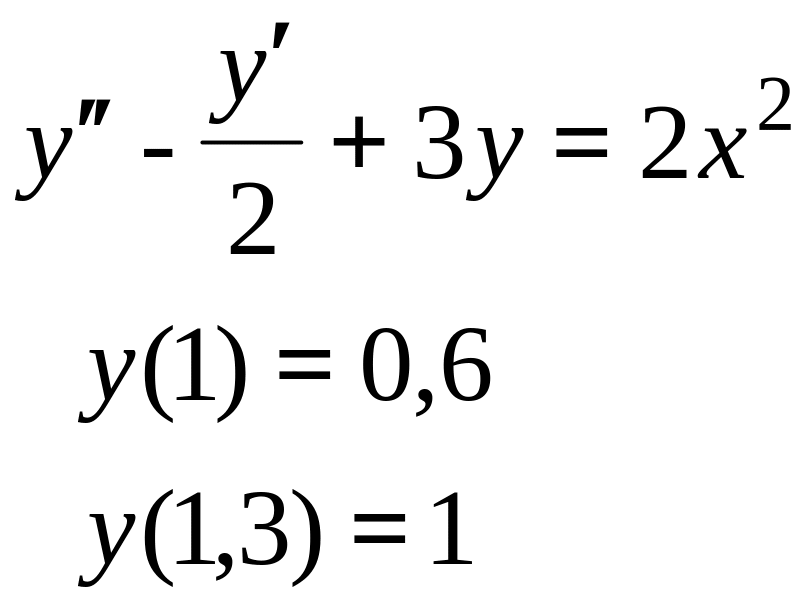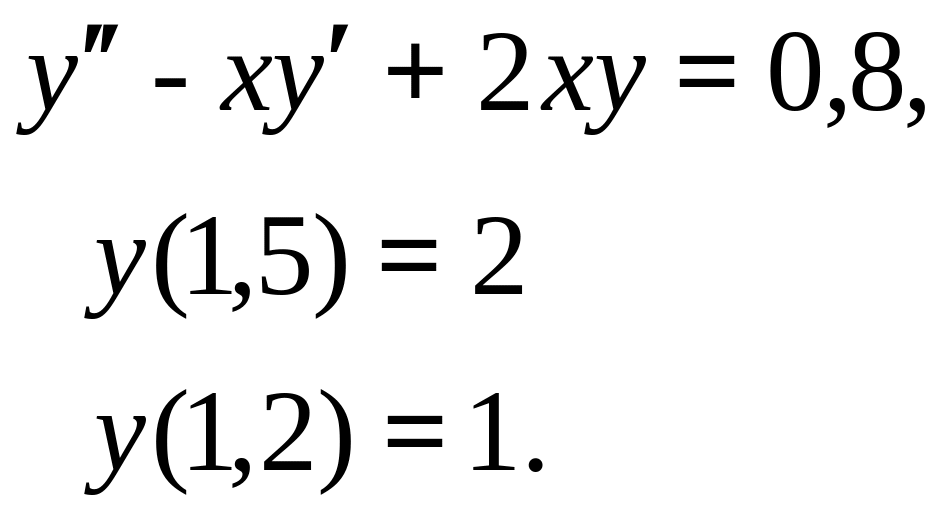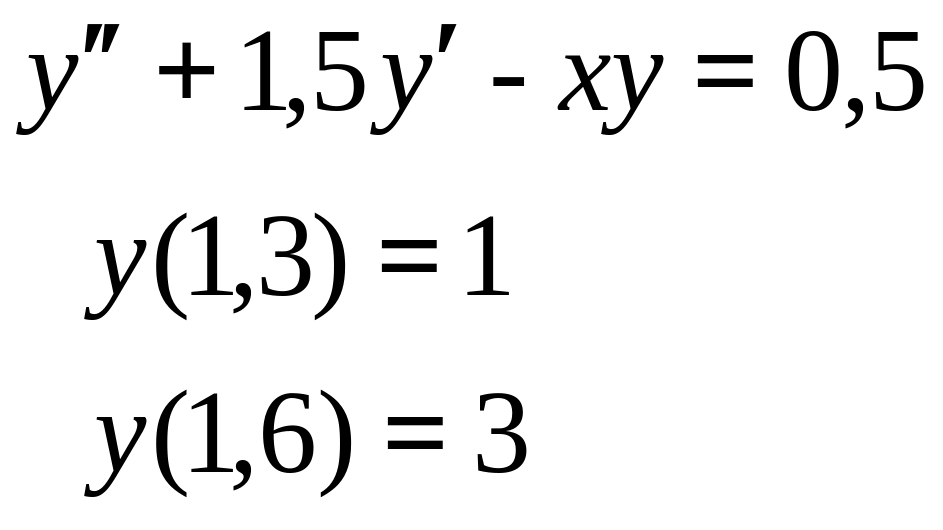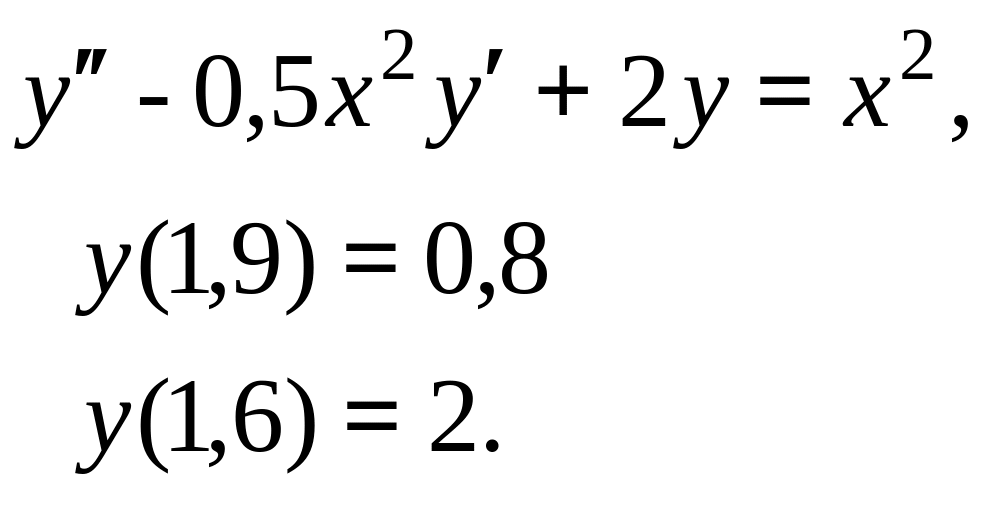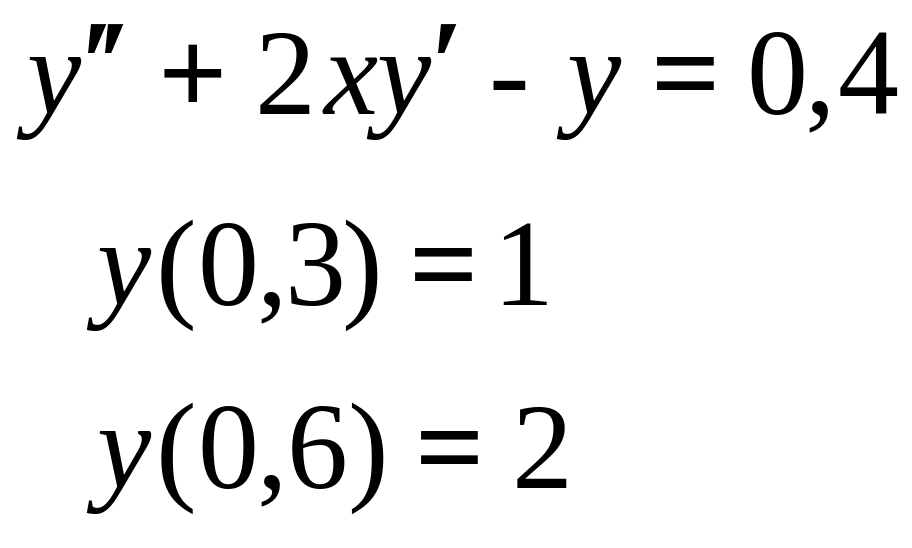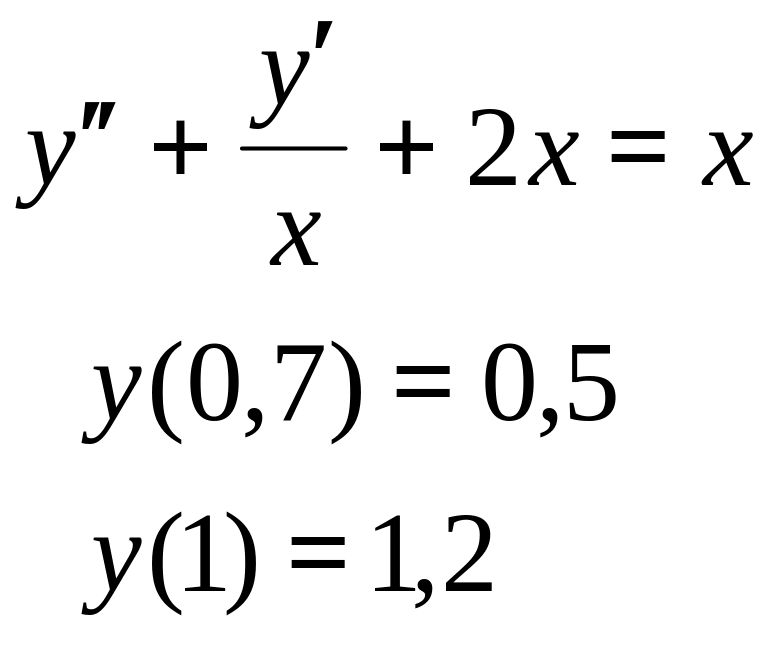Продолжение таблицы 7

Номер варианта	, начальное условие	Номер варианта	, начальное условие
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

2.6 Метод прогонки

Цель работы: используя метод прогонки, решить краевую задачу для дифференциального уравнения 2-го порядка y+p(x)y+q(x)y=f(x) с заданными граничными условиями на отрезке [a,b]. Сравнить полученное численное решение с аналитическим решением. Варианты заданий представлены в таблице 7.

Рекомендация к выполнению задания

Программирование метода производится в среде разработки на выбор студента (Delphi, Borland C++, Turbo Pascal и т. д.).

Входные параметры программы:

дифференциальное уравнение 2-го порядка:

y+p(x)y+q(x)y=f(x);

функциональные коэффициенты р(х), q(х), f(х);

краевые условия;

h – шаг сетки.

Выходные параметры программы:

графическое представление результатов численного решения по методу прогонки.

Отчет по самостоятельной работе должен содержать:

постановку задачи;

блок-схему реализации вычислений значений функции y(x) в узлах сетки по методу прогонки;

программу решения краевой задачи для дифференциального уравнения 2-го порядка с графическим представлением результатов численного и аналитического решений.

Теоретические сведения

Пусть на интервале [a,b] рассматривается краевая задача для дифференциального уравнения 2-го порядка

y+p(x)y+q(x)y=f(x) (34)

с краевыми условиями

, (35)

.

Построим последовательность точек приближения с шагом h:

x_n=x₀+nh, (n=0, 1, 2, …), . (36)

Подменим производные в уравнении (34) конечными разностями с учетом построенной сетки узлов (36). Получим систему линейных алгебраических уравнений, каждое уравнение которой будет связывать три соседних неизвестных:

, (37)

где i=0, 1, 2, …, n; , .

Ниже представлена система линейных уравнений в развернутом виде:

.

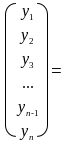
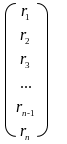Исключим ненулевые элементы в поддиагональной части матрицы коэффициентов системы. Предположим, что существуют такие наборы чисел _i и _i (i=0, 1, 2, …, n) при которых

. (38)

Уменьшим в связи (38) индекс на единицу и представим уравнение (37) в виде

,

откуда

.

Представление (39) имеет место, если и .

В силу условия процесс вычисления _i и _i может быть начат со значений , и далее продолжен по формуле (38). При i=n, в силу , получим . Полагая в (38) i=n, имеем .

Выполняя обратный ход по формуле (38), последовательно найдем y_n-1, y_n-2, y_n-3, …, y₁ при i=n-1, n-2, …, 1 соответственно.

Прямой прогонкой назовем процесс вычисления прогоночных коэффициентов _i и _i.

Обратной прогонкой – процесс вычисления неизвестных y_i по формуле (38).