34. Обратная угловая засечка. Решение задачи Потенота

34. Определение координат промерного судна с берега прямой засечкой с берега.

Исходные данные: xa, ya, αAc, xb, yb, αBd

Измеряемые элементы: β 1 , β2

Неизвестные элементы: X , y

Сначала рассмотрим так называемый общий случай прямой угловой засечки, когда углы β₁ и β₂ измеряются на двух пунктах с известными координатами, каждый от своего направления с известным дирекционным углом (рис. 2.6).

Если α_AC и α_BD не заданы явно, нужно решить обратную геодезическую задачу сначала между пунктами A и C и затем между пунктами B и D .

Графическое решение. От направления AC отложить с помощью транспортира угол β₁ и провести прямую линию AP; от направления BD отложить угол β₂ и провести прямую линию BP ; точка пересечения этих прямых является искомой точкой P.

Аналитическое решение. Приведем алгоритм варианта, соответствующий общему случаю засечки:

1. вычислить дирекционные углы линий AP и BP   (2.14) ,               (2.15)

2. написать два уравнения прямых линий

для линии AP           Y - Y_A= tgα₁ * ( X - X_A ),

для линии BP          Y - Y_B= tgα₂ * ( X - X_B )                         (2.16)

3. решить систему двух уравнений и вычислить неизвестные координаты X и Y:

    (2.17) ,            (2.18)

Частным случаем прямой угловой засечки считают тот случай, когда углы β₁ и β₂ измерены от направлений AB и BA, причем угол β₁ - правый, а угол β₂ - левый (в общем случае засечки оба угла - левые) - рис. 2.7.

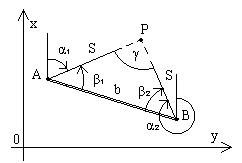Решение прямой угловой засечки методом треугольника соответствует частному случаю засечки. Порядок решения при этом будет такой:

1.решить обратную задачу между пунктами A и B и получить дирекционный угол α_AB и длину b линии AB,

2.вычислить угол γ при вершине P, называемый углом засечки,

            (2.19)

3. используя теорему синусов для треугольника APB:

               (2.20) вычислить длины сторон AP (S₁) и BP (S₂) ,

4. вычислить дирекционные углы α₁ и α₂:                 

5. решить прямую задачу от пункта A к точке P и для контроля - от пункта B к точке P.

Для вычисления координат X и Y в частном случае прямой угловой засечки можно использовать формулы Юнга:

От общего случая прямой угловой засечки нетрудно перейти к частному случаю; для этого нужно сначала решить обратную геодезическую задачу между пунктами A и B и получить дирекционный угол α_AB линии AB и затем вычислить углы в треугольнике APB при вершинах A и B BAP = α_AB - ( α_AC + β₁ ) и ABP = ( α_BD + β₂ ) - α_BA .

34. Определение поправки компаса.

Магнитное склонение d – это угол в плоскости истинного горизонта между географическим (истинным) и магнитным меридианами.

На 1985 г. d = 1о W, годовое изменение d = 0,2o, склонение в 2000 г. - ?

Решение:

Δt = 2000-1985 = 15 лет

d2000 = d + ΔdΔt = +2o E

На судне обычно устанавливают два различных компаса: главный компас для определения места судна и путевой – для управления судном. Главный компас устанавливают в ДП судна, в месте, обеспечивающем круговой обзор и максимальную защищённость от судовых магнитных полей. Обычно – это навигационный мостик судна.

Расчёт девиации: δi = МП - КПi

И составляют таблицу или график девиации как функции компасного курса.

Если производят сличение путевого и главного магнитных компасов или путевого и гирокомпаса, то справедливы соотношения: ККп + δп = ККгл + δгл, ККп + δп = ГКК + ΔГК - d

По требованиям ПДНВ-78/95 требуется, чтобы вахтенный помощник каждые 4 часа определял поправку компаса. Существуют следующие виды вычисления поправок:

1. По створам;

2. По пеленгу удаленного ориентира;

3. С помощью пеленгования светила;

4. По сличению с другим компасом;

5. Методом взаимных пеленгов.